Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-26T00:29:47.223Z Has data issue: false hasContentIssue false
  • English
  • Français

Geodesic flows on manifolds of negative curvature with smooth horospheric foliations†

Published online by Cambridge University Press:  19 September 2008

Renato Feres
Renato Feres
Affiliation:
Mathematical Sciences Research Institute, 1000 Centennial Drive, Berkeley, CA 94720, USA and Universidade Estadual de Campinas, Brazil
Get access Rights & Permissions [Opens in a new window]

Abstract

We improve and extend a result due to M. Kanai about rigidity of geodesic flows on closed Riemannian manifolds of negative curvature whose stable or unstable horospheric foliation is smooth. More precisely, the main results proved here are: (1) Let M be a closed C∞ Riemannian manifold of negative sectional curvature. Assume the stable or unstable foliation of the geodesic flow φt: V → V on the unit tangent bundle V of M is C∞. Assume, moreover, that either (a) the sectional curvature of M satisfies −4 < K ≤ −1 or (b) the dimension of M is odd. Then the geodesic flow of M is C∞-isomorphic (i.e., conjugate under a C∞ diffeomorphism between the unit tangent bundles) to the geodesic flow on a closed Riemannian manifold of constant negative curvature. (2) For M as above, assume instead of (a) or (b) that dim M ≡ 2(mod 4). Then either the above conclusion holds or φ1, is C∞-isomorphic to the flow 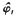, on the quotient Γ\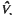, where Γ is a subgroup of a real Lie group 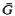⊂ Diffeo (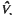) with Lie algebra 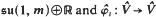is the geodesic flow on the unit tangent bundle of the complex hyperbolic space ℂHm, m = ½ dim M.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 11 , Issue 4 , December 1991 , pp. 653 - 686
Copyright
Copyright © Cambridge University Press 1991

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[A]Anosov, D. V.. Geodesic flows on closed Riemann manifolds with negative curvature. Proc. Steklov Institute of Mathematics 90 (1967).Google Scholar
[BFL]Benoist, Y., Foulon, P. & Labourie, F.. Flots d'Anosov à distributions stable et instable différentiables. Preprint.Google Scholar
[C]Cheng, J. H.. Graded Lie algebras of the second kind. Trans. American Math. Soc. 302 (1987), 467–588.CrossRefGoogle Scholar
[EO]Eberlein, P. & O'Neill, B.. Visibility manifolds. Pacific J. Math. 46 (1973), 45–109.CrossRefGoogle Scholar
[FK1]Feres, R. & Katok, A.. Invariant tensor fields of dynamical systems with pinched Lyapunov exponents and rigidity of geodesic flows. Ergod. Th. & Dynam. Sys. 9 (1989), 427–432.CrossRefGoogle Scholar
[FK2]Feres, R. & Katok, A.. Anosov flows with smooth foliations and rigidity of geodesic flows in three-dimensional manifolds of negative curvature. Ergod. Th. & Dynam. Sys. 10 (1990) 657–670.CrossRefGoogle Scholar
[FL]Foulon, P. & Labourie, F.. Flots d'Anosov à distributions de Liapunov différentiables. Preprint.Google Scholar
[FI.K]Flaminio, L. & Katok, A.. Rigidity of symplectic Anosov diffeomorphisms on low dimensional tori. Ergod. Th. & Dynam. Sys. 11 (1991), 427–440.Google Scholar
[G]Ghys, E.. Flots d'Anosov dont les feuilletages stables sont différentiables. Ann. Sci. École Norm. Sup. (4) 20 (1987), No. 2, 251–270.CrossRefGoogle Scholar
[H]Hasselblatt, B.. Regularity of the Anosov splitting and a new description of the Margulis measure. PhD Thesis, California Institute of Technology (1989).Google Scholar
[HK]Hurder, S. & Katok, A.. Differentiability, rigidity and Godbillon-Vey classes for Anosov flows. Publ. Math. IHES 72 (1990), 5–61.CrossRefGoogle Scholar
[Ht]Heintze, E.. On homogeneous manifolds of negative curvature. Math. Ann. 211 (1974), 23–34.Google Scholar
[K]Kanai, M.. Geodesic flows of negatively curved manifolds with smooth stable and unstable foliations. Ergod. Th. & Dynam. Sys. 8 (1988), 215–240.CrossRefGoogle Scholar
[KA]Kaneyuki, S. & Asano, H.. Graded Lie algebras and generalized Jordan triple systems. Nagoya Math. J. 112 (1988), 81–115.Google Scholar
[Kl]Klingenberg, W.. Riemannian Geometry, de Gruyter Studies in Mathematics, 1982.Google Scholar
[KN]Kobayashi, S. & Nomizu, K.. Foundations of Differential Geometry. Vols. I and II, John Wiley & Sons, 1963.Google Scholar
[M]Mañé, R.. Ergodic Theory and Differential Dynamics. Springer-Verlag, 1987.CrossRefGoogle Scholar
[Ma]Margulis, G.. Certain measures associated with U-flows on compact manifolds. Functional Anal. Appl. 4 (1970), 55–67.Google Scholar
[Mo]Mostow, G. D.. Rigidity of locally symmetric spaces. Ann. Math. Studies 78, Princeton University Press (1973).Google Scholar
[P]Pesin, Ya. B.. Characteristic Lyapunov exponents and smooth ergodic theory. Russian Math. Surveys 32 no. 4 (1977), 55–114.CrossRefGoogle Scholar
[Pu]Pugh, C.. The Morse-Sard Theorem with mixed differentiability. Preprint.Google Scholar
[S]Steenrod, N.. The Topology of Fiber Bundles. Princeton University Press, 1951.Google Scholar
[W]Walters, P.. An Introduction to Ergodic Theory. Springer-Verlag, 1982.CrossRefGoogle Scholar