Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
CARVALHO, MARIA
RODRIGUES, FAGNER B.
and
VARANDAS, PAULO
2022.
A variational principle for the metric mean dimension of free semigroup actions.
Ergodic Theory and Dynamical Systems,
Vol. 42,
Issue. 1,
p.
65.
Bobok, Jozef
Činč, Jernej
Oprocha, Piotr
and
Troubetzkoy, Serge
2022.
Periodic points and shadowing for generic Lebesgue measure-preserving interval maps.
Nonlinearity,
Vol. 35,
Issue. 5,
p.
2535.
Acevedo, Jeovanny Muentes
2022.
Genericity of Continuous Maps with Positive Metric Mean Dimension.
Results in Mathematics,
Vol. 77,
Issue. 1,
Backes, Lucas
and
Rodrigues, Fagner B.
2023.
A Variational Principle for the Metric Mean Dimension of Level Sets.
IEEE Transactions on Information Theory,
Vol. 69,
Issue. 9,
p.
5485.
Rodrigues, Fagner B.
Jacobus, Thomas
and
Silva, Marcus V.
2023.
Some Variational Principles for the Metric Mean Dimension of a Semigroup Action.
Journal of Dynamical and Control Systems,
Vol. 29,
Issue. 3,
p.
919.
Muentes Acevedo, Jeovanny de Jesus
Romaña Ibarra, Sergio Augusto
and
Arias Cantillo, Raibel de Jesus
2024.
Hölder continuous maps on the interval with positive metric mean dimension.
Revista Colombiana de Matemáticas,
Vol. 57,
Issue. Supl,
p.
57.
Lacerda, Gabriel
and
Romaña, Sergio
2024.
Typical Conservative Homeomorphisms Have Total Metric Mean Dimension.
IEEE Transactions on Information Theory,
Vol. 70,
Issue. 11,
p.
7664.
Muentes, J.
Becker, A. J.
Baraviera, A. T.
and
Scopel, É.
2024.
Metric Mean Dimension and Mean Hausdorff Dimension Varying the Metric.
Qualitative Theory of Dynamical Systems,
Vol. 23,
Issue. S1,
Acevedo, Jeovanny M.
Romaña, Sergio
and
Arias, Raibel
2024.
Density of the Level Sets of the Metric Mean Dimension for Homeomorphisms.
Journal of Dynamics and Differential Equations,
Liu, Chunlin
and
Rodrigues, Fagner B.
2024.
Metric Mean Dimension via Preimage Structures.
Journal of Statistical Physics,
Vol. 191,
Issue. 2,
Acevedo, Jeovanny Muentes
2024.
Genericity of Homeomorphisms with Full Mean Hausdorff Dimension.
Regular and Chaotic Dynamics,
Vol. 29,
Issue. 3,
p.
474.
Bobok, Jozef
Činč, Jernej
Oprocha, Piotr
and
Troubetzkoy, Serge
2025.
Continuous Lebesgue measure-preserving maps on one-dimensional manifolds: A survey.
Topology and its Applications,
Vol. 364,
Issue. ,
p.
109101.
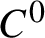 $C^0$
-generic homeomorphisms, acting on a compact smooth boundaryless manifold with dimension greater than one, the upper metric mean dimension with respect to the smooth metric coincides with the dimension of the manifold. As an application, we show that the upper box dimension of the set of periodic points of a
$C^0$
-generic homeomorphisms, acting on a compact smooth boundaryless manifold with dimension greater than one, the upper metric mean dimension with respect to the smooth metric coincides with the dimension of the manifold. As an application, we show that the upper box dimension of the set of periodic points of a 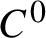 $C^0$
-generic homeomorphism is equal to the dimension of the manifold. In the case of continuous interval maps, we prove that each level set for the metric mean dimension with respect to the Euclidean distance is
$C^0$
-generic homeomorphism is equal to the dimension of the manifold. In the case of continuous interval maps, we prove that each level set for the metric mean dimension with respect to the Euclidean distance is 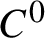 $C^0$
-dense in the space of continuous endomorphisms of
$C^0$
-dense in the space of continuous endomorphisms of 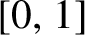 $[0,1]$
with the uniform topology. Moreover, the maximum value is attained at a
$[0,1]$
with the uniform topology. Moreover, the maximum value is attained at a 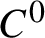 $C^0$
-generic subset of continuous interval maps and a dense subset of metrics topologically equivalent to the Euclidean distance.
$C^0$
-generic subset of continuous interval maps and a dense subset of metrics topologically equivalent to the Euclidean distance.


