Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-23T18:35:44.416Z Has data issue: false hasContentIssue false
  • English
  • Français

Generic chaos on dendrites

Part of: Low-dimensional dynamical systems Topological dynamics

Published online by Cambridge University Press:  19 March 2021

ĽUBOMÍR SNOHA ,
VLADIMÍR ŠPITALSKÝ Open the ORCID record for VLADIMÍR ŠPITALSKÝ [Opens in a new window]  and
MICHAL TAKÁCS
ĽUBOMÍR SNOHA
Affiliation:
Department of Mathematics, Faculty of Natural Sciences, Matej Bel University, Tajovského 40, Banská Bystrica974 01, Slovakia (e-mail: [email protected], [email protected])
VLADIMÍR ŠPITALSKÝ*
Affiliation:
Department of Mathematics, Faculty of Natural Sciences, Matej Bel University, Tajovského 40, Banská Bystrica974 01, Slovakia (e-mail: [email protected], [email protected])
MICHAL TAKÁCS
Affiliation:
Department of Mathematics, Faculty of Natural Sciences, Matej Bel University, Tajovského 40, Banská Bystrica974 01, Slovakia (e-mail: [email protected], [email protected])
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

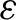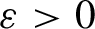We characterize dendrites D such that a continuous selfmap of D is generically chaotic (in the sense of Lasota) if and only if it is generically ${\varepsilon }$ -chaotic for some ${\varepsilon }>0$ . In other words, we characterize dendrites on which generic chaos of a continuous map can be described in terms of the behaviour of subdendrites with non-empty interiors under iterates of the map. A dendrite D belongs to this class if and only if it is completely regular, with all points of finite order (that is, if and only if D contains neither a copy of the Riemann dendrite nor a copy of the 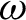$\omega $ -star).

Keywords

completely regular continuumdendritegeneric chaosscrambled pair

MSC classification

Primary: 37B05: Transformations and group actions with special properties (minimality, distality, proximality, etc.)
Secondary: 37B45: Continua theory in dynamics 37E99: None of the above, but in this section
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 42 , Issue 6 , June 2022 , pp. 2108 - 2150
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Dedicated to the memory of Sylvie Ruette

References

Acosta, G., Hernández-Gutiérrez, R., Naghmouchi, I. and Oprocha, P.. Periodic points and transitivity on dendrites. Ergod. Th. & Dynam. Sys. 37(7) (2017), 2017–2033.CrossRefGoogle Scholar
Akin, E., Auslander, J. and Berg, K.. When is a transitive map chaotic? Convergence in Ergodic Theory and Probability (Columbus, OH, 1993) (Ohio State University Mathematical Research Institute Publications, 5). de Gruyter, Berlin, 1996, pp. 25–40.Google Scholar
Akin, E. and Kolyada, S.. Li–Yorke sensitivity. Nonlinearity 16(4) (2003), 1421–1433.CrossRefGoogle Scholar
Arévalo, D., Charatonik, W. J., Pellicer Covarrubias, P. and Simón, L.. Dendrites with a closed set of end points. Topology Appl. 115(1) (2001), 1–17.CrossRefGoogle Scholar
Auslander, J.. Minimal Flows and Their Extensions. North-Holland, Amsterdam, 1988.Google Scholar
Balibrea, F., Downarowicz, T., Hric, R., Snoha, Ľ. and Špitalský, V.. Almost totally disconnected minimal systems. Ergod. Th. & Dynam. Sys. 29 (3) (2009), 737–766.CrossRefGoogle Scholar
Barge, M.. The topological entropy of homeomorphisms of Knaster continua. Houston J. Math. 13(4) (1987), 465–485.Google Scholar
Barge, M., Bruin, H. and Štimac, S.. The Ingram conjecture. Geom. Topol. 16(4) (2012), 2481–2516.CrossRefGoogle Scholar
Blanchard, F., Glasner, E., Kolyada, S. and Maass, A.. On Li–Yorke pairs. J. Reine Angew. Math. 547 (2002), 51–68.Google Scholar
Blanchard, F., Huang, W. and Snoha, Ľ.. Topological size of scrambled sets. Colloq. Math. 110(2) (2008), 293–361.CrossRefGoogle Scholar
Blokh, A. M., Fokkink, R. J., Mayer, J. C., Oversteegen, L. G. and Tymchatyn, E. D.. Fixed Point Theorems for Plane Continua with Applications (Memoirs of the American Mathematical Society, 224(1053)). American Mathematical Society, Providence, RI, 2013.Google Scholar
Buskirk, R. D., Nikiel, J. and Tymchatyn, E. D.. Totally regular curves as inverse limits. Houston J. Math. 18(3) (1992), 319–327.Google Scholar
Byszewski, J., Falniowski, F. and Kwietniak, D.. Transitive dendrite map with zero entropy. Ergod. Th. & Dynam. Sys. 37(7) (2017), 2077–2083.CrossRefGoogle Scholar
Charatonik, J. J. and Charatonik, W. J.. Dendrites. XXX National Congr. Mexican Mathematical Society (Aguascalientes, 1997) (Aportaciones Matematicas: Comunicaciones, 22). Sociedad Matemática Mexicana, México, 1998, pp. 227–253 (in Spanish).Google Scholar
Chudziak, J., Snoha, Ľ. and Špitalský, V.. From a Floyd–Auslander minimal system to an odd triangular map. J. Math. Anal. Appl. 296(2) (2004), 393–402.CrossRefGoogle Scholar
Dirbák, M., Snoha, Ľ. and Špitalský, V.. Minimality, transitivity, mixing and topological entropy on spaces with a free interval. Ergod. Th. & Dynam. Sys. 33(6) (2013), 1786–1812.CrossRefGoogle Scholar
Eilenberg, S.. Continua of finite linear measure II. Amer. J. Math. 66 (1944), 425–427.CrossRefGoogle Scholar
Floyd, E. E.. A nonhomogeneous minimal set. Bull. Amer. Math. Soc. 55 (1949), 957–960.CrossRefGoogle Scholar
Forti, G. L., Paganoni, L. and Smítal, J., Dynamics of homeomorphisms on minimal sets generated by triangular mappings. Bull. Aust. Math. Soc. 59 (1999), 1–20.CrossRefGoogle Scholar
Gehman, H. M.. Concerning the subsets of a plane continuous curve. Ann. of Math. (2) 27(1) (1925), 29–46.CrossRefGoogle Scholar
Glasner, E. and Megrelishvili, M.. Group actions on treelike compact spaces. Sci. China Math. 62(12) (2019), 2447–2462.CrossRefGoogle Scholar
Glasner, E. and Weiss, B.. Sensitive dependence on initial conditions. Nonlinearity 6(6) (1993), 1067–1075.CrossRefGoogle Scholar
Haddad, K. N. and Johnson, A. S. A.. Auslander systems. Proc. Amer. Math. Soc. 125(7) (1997), 2161–2170.CrossRefGoogle Scholar
Handel, M.. A pathological area preserving ${\mathrm{C}}^{\infty }$ diffeomorphism of the plane. Proc. Amer. Math. Soc. 86(1) (1982), 163–168.Google Scholar
Harrold, O. G.. The construction of a certain metric. Duke Math. J. 11 (1944), 23–34.CrossRefGoogle Scholar
Hoehn, L. and Mouron, C.. Hierarchies of chaotic maps on continua. Ergod. Th. & Dynam. Sys. 34(6) (2014), 1897–1913.CrossRefGoogle Scholar
Huang, W. and Ye, X.. Homeomorphisms with the whole compacta being scrambled sets. Ergod. Th. & Dynam. Sys. 21(1) (2001), 77–91.CrossRefGoogle Scholar
Huang, W. and Ye, X.. Devaney’s chaos or 2-scattering implies Li–Yorke’s chaos. Topology Appl. 117(3) (2002), 259–272.CrossRefGoogle Scholar
Iliadis, S. D.. Universal continuum for the class of completely regular continua. Bull. Acad. Polon. Sci. Sér. Sci. Math. 28(11–12) (1980), 603–607.Google Scholar
Illanes, A.. A characterization of dendrites with the periodic-recurrent property. Topology Proc. 23 Summer (1998), 221–235.Google Scholar
Ingram, W. T. and Mahavier, W. S.. Inverse Limits. From Continua to Chaos (Developments in Mathematics, 25). Springer, New York, NY, 2012.Google Scholar
Kato, H.. Topological entropy and IE-tuples of indecomposable continua. Fund. Math. 247(2) (2019), 131–149.CrossRefGoogle Scholar
Kato, H. and Mouron, C.. Hereditarily indecomposable compacta do not admit expansive homeomorphisms. Proc. Amer. Math. Soc. 136(10) (2008), 3689–3696.CrossRefGoogle Scholar
Kennedy, J.. A transitive homeomorphism on the pseudoarc which is semiconjugate to the tent map. Trans. Amer. Math. Soc. 326(2) (1991), 773–793.CrossRefGoogle Scholar
Kočan, Z.. Chaos on one-dimensional compact metric spaces. Internat. J. Bifur. Chaos Appl. Sci. Engrg. 22(10) (2012), 1250259, 10 pp.CrossRefGoogle Scholar
Kuchta, M. and Smítal, J.. Two-point scrambled set implies chaos. Eur. Conf. Iteration Theory (Caldes de Malavella, 1987). World Scientific, Teaneck, NJ, 1989, pp. 427–430.Google Scholar
Kuratowski, K.. Topology, Vol. II. Academic Press, New York; Państwowe Wydawnictwo Naukowe, Warsaw, 1968.Google Scholar
Levin, G. and van Strien, S.. Local connectivity of the Julia set of real polynomials. Ann. of Math. (2) 147(3) (1998), 471–541.CrossRefGoogle Scholar
Martínez-de-la-Vega, V.. A strong characterization on the $\Omega$ EP-property. Topology Appl. 154(17) (2007), 3032–3038.CrossRefGoogle Scholar
Murinová, E.. Generic chaos in metric spaces. Acta Univ. M. Belii Ser. Math. 8 (2000), 43–50.Google Scholar
Li, T. Y. and Yorke, J. A.. Period three implies chaos. Amer. Math. Monthly 82(10) (1975), 985–992.CrossRefGoogle Scholar
Mouron, C.. Tree-like continua do not admit expansive homeomorphisms. Proc. Amer. Math. Soc. 130(11) (2002), 3409–3413.CrossRefGoogle Scholar
Mouron, C.. Positive entropy homeomorphisms of chainable continua and indecomposable subcontinua. Proc. Amer. Math. Soc. 139(8) (2011), 2783–2791.CrossRefGoogle Scholar
Nadler, S. B. Jr.. Continuum Theory. An Introduction (Monographs and Textbooks in Pure and Applied Mathematics, 158). Marcel Dekker, New York, NY, 1992.Google Scholar
Nikiel, J.. Locally connected curves viewed as inverse limits. Fund. Math. 133(2) (1989), 125–134.CrossRefGoogle Scholar
Omiljanowski, K. and Zafiridou, S.. Universal completely regular dendrites. Colloq. Math. 103(1) (2005), 149–154.CrossRefGoogle Scholar
Piórek, J.. On the generic chaos in dynamical systems. Univ. Iagel. Acta Math. 25 (1985), 293–298.Google Scholar
Plykin, R. V.. The geometry of hyperbolic attractors of smooth cascades. Uspekhi Mat. Nauk 39(6(240)) (1984), 75–113 (in Russian).Google Scholar
Roth, S.. Dynamics on dendrites with closed endpoint sets. Nonlinear Anal. 195 (2020), 111745, 13 pp.CrossRefGoogle Scholar
Ruette, S.. Chaos on the Interval (University Lecture Series, 67). American Mathematical Society, Providence, RI, 2017.Google Scholar
Ruette, S. and Snoha, Ľ.. For graph maps, one scrambled pair implies Li–Yorke chaos. Proc. Amer. Math. Soc. 142(6) (2014), 2087–2100.CrossRefGoogle Scholar
Schirmer, H.. Effluent and noneffluent fixed points on dendrites. Pacific J. Math. 75(2) (1978), 539–552.CrossRefGoogle Scholar
Seidler, G. T.. The topological entropy of homeomorphisms on one-dimensional continua. Proc. Amer. Math. Soc. 108(4) (1990), 1025–1030.CrossRefGoogle Scholar
Smítal, J.. Chaotic functions with zero topological entropy. Trans. Amer. Math. Soc. 297(1) (1986), 269–282.CrossRefGoogle Scholar
Snoha, Ľ.. Generic chaos. Comment. Math. Univ. Carolin. 31(4) (1990), 793–810.Google Scholar
Snoha, Ľ.. Dense chaos. Comment. Math. Univ. Carolin. 33(4) (1992), 747–752.Google Scholar
Špitalský, V.. Omega-limit sets in hereditarily locally connected continua. Topology Appl. 155(11) (2008), 1237–1255.CrossRefGoogle Scholar
Špitalský, V.. Length-expanding Lipschitz maps on totally regular continua. J. Math. Anal. Appl. 412(1) (2014), 15–28.CrossRefGoogle Scholar
Takács, M.. Generic chaos on graphs. J. Difference Equ. Appl. 22(1) (2016), 1–21.CrossRefGoogle Scholar
Whyburn, G. T.. Analytic Topology (American Mathematical Society Colloquium Publications, 28). American Mathematical Society, New York, NY, 1942.Google Scholar
Williams, R. F.. A note on unstable homeomorphisms. Proc. Amer. Math. Soc. 6 (1955), 308–309.CrossRefGoogle Scholar