Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-24T15:51:00.419Z Has data issue: false hasContentIssue false
  • English
  • Français

The Furstenberg–Poisson boundary and CAT(0) cube complexes

Published online by Cambridge University Press:  02 May 2017

TALIA FERNÓS
TALIA FERNÓS*
Affiliation:
Department of Mathematics and Statistics, University of North Carolina at Greensboro, 317 College Avenue, Greensboro, NC 27412, USA email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

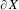We show under weak hypotheses that $\unicode[STIX]{x2202}X$, the Roller boundary of a finite-dimensional CAT(0) cube complex 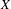$X$ is the Furstenberg–Poisson boundary of a sufficiently nice random walk on an acting group 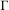$\unicode[STIX]{x1D6E4}$. In particular, we show that if 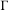$\unicode[STIX]{x1D6E4}$ admits a non-elementary proper action on 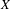$X$, and $\unicode[STIX]{x1D707}$ is a generating probability measure of finite entropy and finite first logarithmic moment, then there is a $\unicode[STIX]{x1D707}$-stationary measure on 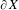$\unicode[STIX]{x2202}X$ making it the Furstenberg–Poisson boundary for the $\unicode[STIX]{x1D707}$-random walk on 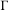$\unicode[STIX]{x1D6E4}$. We also show that the support is contained in the closure of the regular points. Regular points exhibit strong contracting properties.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 38 , Issue 6 , September 2018 , pp. 2180 - 2223
Copyright
© Cambridge University Press, 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aaronson, J.. An Introduction to Infinite Ergodic Theory (Mathematical Surveys and Monographs, 50) . American Mathematical Society, Providence, RI, 1997.Google Scholar
Adams, S. and Ballmann, W.. Amenable isometry groups of Hadamard spaces. Math. Ann. 312(1) (1998), 183–195.Google Scholar
Agol, I.. The virtual Haken conjecture. Doc. Math. 18 (2013), 1045–1087. With an appendix by Agol, Daniel Groves, and Jason Manning.Google Scholar
Behrstock, J. and Charney, R.. Divergence and quasimorphisms of right-angled Artin groups. Math. Ann. 352(2) (2012), 339–356.Google Scholar
Brodzki, J., Campbell, S. J., Guentner, E., Niblo, G. A. and Wright, N. J.. Property A and CAT(0) cube complexes. J. Funct. Anal. 256(5) (2009), 1408–1431.Google Scholar
Bader, U. and Furman, A.. Boundaries, rigidity of representations, and Lyapunov exponents. Proc. ICM (2014), 22pp.Google Scholar
Bridson, M. R. and Haefliger, A.. Metric Spaces of Non-Positive Curvature (Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], 319) . Springer, Berlin, 1999.Google Scholar
Bowditch, B. H.. A topological characterisation of hyperbolic groups. J. Amer. Math. Soc. 11(3) (1998), 643–667.Google Scholar
Bader, U. and Shalom, Y.. Factor and normal subgroup theorems for lattices in products of groups. Invent. Math. 163(2) (2006), 415–454.Google Scholar
Bergeron, N. and Wise, D. T.. A boundary criterion for cubulation. Amer. J. Math. 134(3) (2012), 843–859.Google Scholar
Chatterji, I., Ferns, T. and Iozzi, A.. The median class and superrigidity of actions on CAT(0) cube complexes. J. Topol. 9(2) (2016), 349–400; with an appendix by P.-E. Caprace.Google Scholar
Caprace, P.-E. and Lytchak, A.. An infinity of finite-dimensional CAT(0) spaces. Math. Ann. 346(1) (2010), 1–21.Google Scholar
Caprace, P.-E. and Lécureux, J.. Combinatorial and group-theoretic compactifications of buildings. Ann. Inst. Fourier (Grenoble) 61(2) (2011), 619–672.Google Scholar
Caprace, P.-E. and Monod, N.. Fixed points and amenability in non-positive curvature. Math. Ann. 356(4) (2013), 1303–1337.Google Scholar
Chatterji, I. and Niblo, G.. From wall spaces to CAT(0) cube complexes. Internat. J. Algebra Comput. 15(5–6) (2005), 875–885.Google Scholar
Caprace, P.-E. and Sageev, M.. Rank rigidity for CAT(0) cube complexes. Geom. Funct. Anal. 21(4) (2011), 851–891.Google Scholar
Derriennic, Y. and Guivarc’h, Y.. Théorème de renouvellement pour les groupes non moyennables. C. R. Acad. Sci. Paris Sér. A-B 277 (1973), A613–A615.Google Scholar
Furman, A.. Random walks on groups and random transformations. Handbook of Dynamical Systems. Vol. 1A. North-Holland, Amsterdam, 2002, pp. 931–1014.Google Scholar
Furstenberg, H.. Boundary theory and stochastic processes on homogeneous spaces. Harmonic Analysis on Homogeneous Spaces (Proc. Symp. Pure Math., Vol. XXVI, Williams Coll., Williamstown, MA, 1972). American Mathematical Society, Providence, RI, 1973, pp. 193–229.Google Scholar
Haglund, F. and Wise, D. T.. Special cube complexes. Geom. Funct. Anal. 17(5) (2008), 1551–1620.Google Scholar
Kaimanovich, V. A.. Double ergodicity of the Poisson boundary and applications to bounded cohomology. Geom. Funct. Anal. 13(4) (2003), 852–861.Google Scholar
Kaimanovich, V. A.. The Poisson boundary of hyperbolic groups. C. R. Acad. Sci. Paris Sér. I Math. 318(1) (1994), 59–64.Google Scholar
Kahn, J. and Markovic, V.. Immersing almost geodesic surfaces in a closed hyperbolic three manifold. Ann. of Math. (2) 175(3) (2012), 1127–1190.Google Scholar
Karlsson, A. and Margulis, G. A.. A multiplicative ergodic theorem and nonpositively curved spaces. Comm. Math. Phys. 208(1) (1999), 107–123.Google Scholar
Nica, B.. Cubulating spaces with walls. Algebr. Geom. Topol. 4 (2004), 297–309 (electronic).Google Scholar
Nevo, A. and Sageev, M.. The Poisson boundary of CAT(0) cube complex groups. Groups Geom. Dyn. 7(3) (2013), 653–695.Google Scholar
Pays, I. and Valette, A.. Sous-groupes libres dans les groupes d’automorphismes d’arbres. Enseign. Math. (2) 37(1–2) (1991), 151–174.Google Scholar
Roller, M.. Poc sets, median algebras and group actions. An extended study of Dunwoody’s construction and Sageev’s theorem. Southampton Preprint Archive, 1998, https://arxiv.org/abs/1607.07747.Google Scholar
Ruane, K. and Witzel, S.. CAT(0) cubical complexes for graph products of finitely generated abelian groups. New York J. Math. 22 (2016), 637–651.Google Scholar
Sageev, M.. Ends of group pairs and non-positively curved cube complexes. Proc. Lond. Math. Soc. (3) 71(3) (1995), 585–617.Google Scholar
Sageev, M. and Wise, D. T.. The Tits alternative for CAT(0) cubical complexes. Bull. Lond. Math. Soc. 37(5) (2005), 706–710.Google Scholar
Wise, D. T.. Research announcement: the structure of groups with a quasiconvex hierarchy. Electron. Res. Announc. Math. Sci. 16 (2009), 44–55.Google Scholar