Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-26T01:38:57.764Z Has data issue: false hasContentIssue false
  • English
  • Français

Furstenberg maps for CAT(0) targets of finite telescopic dimension

Published online by Cambridge University Press:  13 April 2015

URI BADER ,
BRUNO DUCHESNE  and
JEAN LÉCUREUX
URI BADER
Affiliation:
Mathematics Department, Technion - Israel Institute of Technology, Haifa, 32000, Israel email [email protected]
BRUNO DUCHESNE
Affiliation:
Institut Élie Cartan de Lorraine, Université de Lorraine, B.P. 70239, F-54506 Vandoeuvre-lès-Nancy Cedex, France email [email protected]
JEAN LÉCUREUX
Affiliation:
Département de Mathématiques - Bâtiment 425, Faculté des Sciences d’Orsay, Université Paris-Sud 11, F-91405 Orsay, France email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider actions of locally compact groups 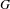$G$ on certain CAT(0) spaces 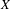$X$ by isometries. The CAT(0) spaces we consider have finite dimension at large scale. In case 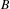$B$ is a 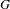$G$-boundary, that is a measurable 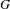$G$-space with some amenability and ergodicity properties, we prove the existence of equivariant maps from 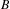$B$ to the visual boundary 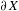$\partial X$.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 36 , Issue 6 , September 2016 , pp. 1723 - 1742
Copyright
© Cambridge University Press, 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

A’Campo, N. and Burger, M.. Réseaux arithmétiques et commensurateur d’après G. A. Margulis. Invent. Math. 116(1–3) (1994), 1–25.Google Scholar
Adams, S. and Ballmann, W.. Amenable isometry groups of Hadamard spaces. Math. Ann. 312(1) (1998), 183–195.Google Scholar
Anderegg, M. and Henry, P.. Actions of amenable equivalence relations on CAT(0) fields. Ergod. Th. & Dynam. Sys. 34(1) (2014), 21–54.Google Scholar
Bader, U. and Furman, A.. Algebraic representations of ergodic actions and super-rigidity. Preprint, 2013,arXiv:1311.3696.Google Scholar
Bader, U. and Furman, A.. Boundaries, rigidity of representations, and Lyapunov exponents. Proc. ICM 2014, 27pp, Preprint, 2014, arXiv:1404.5107.Google Scholar
Bader, U. and Furman, A.. Boundaries, Weyl groups, and superrigidity. Electron. Res. Announc. Math. Sci. 19 (2012), 41–48.Google Scholar
Bridson, M. R. and Haefliger, A.. Metric Spaces of Non-Positive Curvature (Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], 319) . Springer, Berlin, 1999.Google Scholar
Burger, M. and Monod, N.. Continuous bounded cohomology and applications to rigidity theory. Geom. Funct. Anal. 12(2) (2002), 219–280.Google Scholar
Caprace, P.-E. and Lytchak, A.. Erratum to ‘At Infinity of finite-dimensional CAT(0) spaces’ (unpublished).Google Scholar
Caprace, P.-E. and Lytchak, A.. At infinity of finite-dimensional CAT(0) spaces. Math. Ann. 346(1) (2010), 1–21.Google Scholar
Caprace, P.-E. and Monod, N.. Isometry groups of non-positively curved spaces: structure theory. J. Topol. 2(4) (2009), 661–700.Google Scholar
Duchesne, B.. Infinite dimensional Riemannian symmetric spaces with fixed-sign curvature operator.Ann. Inst. Fourier (Grenoble), to appear, Preprint, 2012, arXiv:1204.6012.Google Scholar
Duchesne, B.. Infinite-dimensional nonpositively curved symmetric spaces of finite rank. Int. Math. Res. Not. IMRN(7) (2013), 1578–1627.Google Scholar
Fremlin, D. H.. Measurable functions and almost continuous functions. Manuscripta Math. 33(3–4) (1980/81), 387–405.Google Scholar
Furstenberg, H.. A Poisson formula for semi-simple Lie groups. Ann. of Math. (2) 77 (1963), 335–386.Google Scholar
Furstenberg, H.. Boundary theory and stochastic processes on homogeneous spaces. Harmonic Analysis on Homogeneous Spaces (Proc. Sympos Pure Math. XXVI, Williams Coll., Williamstown, MA, 1972) . American Mathematical Society, Providence, RI, 1973, pp. 193–229.Google Scholar
Gromov, M.. Asymptotic invariants of infinite groups. Geometric Group Theory, Vol. 2 (Sussex, 1991) (London Mathematical Society, Lecture Note Series, 182) . Cambridge University Press, Cambridge, 1993, pp. 1–295.Google Scholar
Jaworski, W.. Strongly approximately transitive group actions, the Choquet–Deny theorem, and polynomial growth. Pacific J. Math. 165(1) (1994), 115–129.Google Scholar
Jung, H. W. E.. Über die kleinste kugel, die eine räumliche figur einschliesst. J. Reine Angew. Math. 123 (1901), 241–257.Google Scholar
Kaimanovich, V. A.. Double ergodicity of the Poisson boundary and applications to bounded cohomology. Geom. Funct. Anal. 13(4) (2003), 852–861.Google Scholar
Kaimanovich, V. A.. The Poisson formula for groups with hyperbolic properties. Ann. of Math. (2) 152(3) (2000), 659–692.Google Scholar
Karlsson, A. and Margulis, G. A.. A multiplicative ergodic theorem and nonpositively curved spaces. Comm. Math. Phys. 208(1) (1999), 107–123.Google Scholar
Kechris, A. S.. Classical Descriptive Set Theory (Graduate Texts in Mathematics, 156) . Springer, New York, 1995.Google Scholar
Kleiner, B.. The local structure of length spaces with curvature bounded above. Math. Z. 231(3) (1999), 409–456.Google Scholar
Lang, U. and Schroeder, V.. Jung’s theorem for Alexandrov spaces of curvature bounded above. Ann. Global Anal. Geom. 15(3) (1997), 263–275.CrossRefGoogle Scholar
Margulis, G. A.. Discrete Subgroups of Semisimple Lie Groups (Ergebnisse der Mathematik und ihrer Grenzgebiete (3) [Results in Mathematics and Related Areas (3)], 17) . Springer, Berlin, 1991.CrossRefGoogle Scholar
Monod, N.. Superrigidity for irreducible lattices and geometric splitting. J. Amer. Math. Soc. 19(4) (2006), 781–814.CrossRefGoogle Scholar
Valadier, M.. Sur le plongement d’un champ mesurable d’espaces métriques dans un champ trivial. Annales de l’I.H.P. B 14(2) (1978), 165–168.Google Scholar
Zimmer, R. J.. Amenable ergodic group actions and an application to Poisson boundaries of random walks. J. Funct. Anal. 27(3) (1978), 350–372.Google Scholar
Zimmer, R. J.. Ergodic Theory and Semisimple Groups (Monographs in Mathematics, 81) . Birkhäuser, Basel, 1984.Google Scholar