Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-24T16:35:59.607Z Has data issue: false hasContentIssue false
  • English
  • Français

Fully essential dynamics for area-preserving surface homeomorphisms

Published online by Cambridge University Press:  14 February 2017

ANDRES KOROPECKI  and
FABIO ARMANDO TAL
ANDRES KOROPECKI
Affiliation:
Universidade Federal Fluminense, Instituto de Matemática e Estatística, Rua Mário Santos Braga S/N, 24020-140 Niteroi, RJ, Brasil email [email protected]
FABIO ARMANDO TAL
Affiliation:
Instituto de Matemática e Estatística, Universidade de São Paulo, Rua do Matão 1010, Cidade Universitária, 05508-090 São Paulo, SP, Brazil email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the interplay between the dynamics of area-preserving surface homeomorphisms homotopic to the identity and the topology of the surface. We define fully essential dynamics and generalize the results previously obtained on strictly toral dynamics to surfaces of higher genus. Non-fully essential dynamics are, in a way, reducible to surfaces of lower genus, while in the fully essential case the dynamics is decomposed into a disjoint union of periodic bounded disks and a complementary invariant externally transitive continuum $C$. When the Misiurewicz–Ziemian rotation set has non-empty interior the dynamics is fully essential, and the set 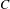$C$ is (externally) sensitive on initial conditions and realizes all of the rotational dynamics. As a fundamental tool we introduce the notion of homotopically bounded sets and we prove a general boundedness result for invariant open sets when the fixed point set is inessential.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 38 , Issue 5 , August 2018 , pp. 1791 - 1836
Copyright
© Cambridge University Press, 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Addas-Zanata, S.. Area-preserving diffeomorphisms of the torus whose rotation sets have non-empty interior. Ergod. Th. & Dynam. Sys. 35 (2015), 1–33.CrossRefGoogle Scholar
Addas-Zanata, S.. On the existence of a new type of periodic and quasi-periodic orbits for twist maps of the torus. Nonlinearity 15(5) (2002), 1399–1416.CrossRefGoogle Scholar
Béguin, F., Crovisier, S. and Le Roux, F.. Pseudo-rotations of the open annulus. Bull. Braz. Math. Soc. (N.S.) 37(2) (2006), 275–306.CrossRefGoogle Scholar
Bonatti, C., Crovisier, S. and Wilkinson, A.. C 1 -generic conservative diffeomorphisms have trivial centralizer. J. Mod. Dyn. 2(2) (2008), 359–373.Google Scholar
Brown, M. and Kister, J. M.. Invariance of complementary domains of a fixed point set. Proc. Amer. Math. Soc. 91(3) (1984), 503–504.Google Scholar
Brown, M.. Homeomorphisms of two-dimensional manifolds. Houston J. Math. 11(4) (1985), 455–469.Google Scholar
Casson, A. J. and Bleiler, S. A.. Automorphisms of surfaces after Nielsen and Thurston. (London Mathematical Society Student Texts, 9) . Cambridge University Press, Cambridge, 1988.Google Scholar
Dávalos, P.. On torus homeomorphisms whose rotation set is an interval. Math. Z. 275(3–4) (2013), 1005–1045.CrossRefGoogle Scholar
Epstein, D. B. A.. Curves on 2-manifolds and isotopies. Acta Math. 115 (1966), 83–107.CrossRefGoogle Scholar
Farb, B. and Margalit, D.. A Primer on Mapping Class Groups (Princeton Mathematical Series, 49) . Princeton University Press, Princeton, NJ, 2012.Google Scholar
Franks, J.. Generalizations of the Poincaré–Birkhoff theorem. Ann. of Math. (2) 128(1) (1988), 139–151.CrossRefGoogle Scholar
Franks, J.. Realizing rotation vectors for torus homeomorphisms. Trans. Amer. Math. Soc. 311(1) (1989), 107–115.CrossRefGoogle Scholar
Franks, J.. Rotation vectors and fixed points of area preserving surface diffeomorphisms. Trans. Amer. Math. Soc. 348(7) (1996), 2637–2662.CrossRefGoogle Scholar
Guelman, N., Koropecki, A. and Tal, F. A.. A characterization of annularity for area-preserving toral homeomorphisms. Math. Z. 276(3–4) (2014), 673–689.CrossRefGoogle Scholar
Guelman, N., Koropecki, A. and Tal, F. A.. Rotation sets with non-empty interior and transitivity in the universal covering. Ergod. Th. & Dynam. Sys. 35(3) (2015), 883–894.CrossRefGoogle Scholar
Gromov, M.. Metric structures for Riemannian and non-Riemannian spaces. Modern Birkhäuser Classics. Birkhäuser, Boston, MA, 2007, Based on the 1981 French original, With appendices by M. Katz, P. Pansu and S. Semmes, translated from the French by Sean Michael Bates.Google Scholar
Hamstrom, M.-E.. Homotopy groups of the space of homeomorphisms on a 2-manifold. Illinois J. Math. 10 (1966), 563–573.CrossRefGoogle Scholar
Handel, M.. The rotation set of a homeomorphism of the annulus is closed. Comm. Math. Phys. 127(2) (1990), 339–349.CrossRefGoogle Scholar
Jäger, T.. Elliptic stars in a chaotic night. J. Lond. Math. Soc. (2) 84(3) (2011), 595–611.CrossRefGoogle Scholar
Jaulent, O.. Existence d’un feuilletage positivement transverse à un homéomorphisme de surface. Ann. Inst. Fourier (Grenoble) 64(4) (2014), 1441–1476.CrossRefGoogle Scholar
Jezierski, J. and Marzantowicz, W.. Homotopy methods in topological fixed and periodic points theory. Topological Fixed Point Theory and Its Applications, Vol. 3. Springer, Dordrecht, 2006.Google Scholar
Koropecki, A., Le Calvez, P. and Nassiri, M.. Prime ends rotation numbers and periodic points. Duke Math. J. 164(3) (2015), 403–472.CrossRefGoogle Scholar
Koropecki, A.. Aperiodic invariant continua for surface homeomorphisms. Math. Z. 266(1) (2010), 229–236.CrossRefGoogle Scholar
Koropecki, A. and Tal, F. A.. Area-preserving irrotational diffeomorphisms of the torus with sublinear diffusion. Proc. Amer. Math. Soc. 142(10) (2014), 3483–3490.CrossRefGoogle Scholar
Koropecki, A. and Tal, F. A.. Bounded and unbounded behavior for area-preserving rational pseudo-rotations. Proc. Lond. Math. Soc. (3) 109(3) (2014), 785–822.CrossRefGoogle Scholar
Koropecki, A. and Tal, F. A.. Strictly toral dynamics. Invent. Math. 196(2) (2014), 339–381.CrossRefGoogle Scholar
Le Calvez, P.. Une version feuilletée équivariante du théorème de translation de Brouwer. Publ. Math. Inst. Hautes Études Sci.(102) (2005), 1–98.CrossRefGoogle Scholar
Llibre, J. and MacKay, R. S.. Rotation vectors and entropy for homeomorphisms of the torus isotopic to the identity. Ergod. Th. & Dynam. Sys. 11(1) (1991), 115–128.CrossRefGoogle Scholar
Misiurewicz, M. and Ziemian, K.. Rotation sets for maps of tori. J. Lond. Math. Soc. (2) 40(3) (1989), 490–506.CrossRefGoogle Scholar
Pollicott, M.. Rotation sets for homeomorphisms and homology. Trans. Amer. Math. Soc. 331(2) (1992), 881–894.CrossRefGoogle Scholar
Richards, I.. On the classification of noncompact surfaces. Trans. Amer. Math. Soc. 106 (1963), 259–269.CrossRefGoogle Scholar
Tal, F. A.. On non-contractible periodic orbits for surface homeomorphisms. Ergod. Th. & Dynam. Sys. 36 (2016), 1644–1655.CrossRefGoogle Scholar
Whitney, H.. Regular families of curves. Ann. of Math. (2) 34(2) (1933), 244–270.CrossRefGoogle Scholar