No CrossRef data available.
Published online by Cambridge University Press: 02 October 2014
We study full groups of minimal actions of countable groups by homeomorphisms on a Cantor space 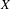 $X$, showing that these groups do not admit a compatible Polish group topology and, in the case of
$X$, showing that these groups do not admit a compatible Polish group topology and, in the case of  $\mathbb{Z}$-actions, are coanalytic non-Borel inside
$\mathbb{Z}$-actions, are coanalytic non-Borel inside  $\text{Homeo}(X)$. We point out that the full group of a minimal homeomorphism is topologically simple. We also study some properties of the closure of the full group of a minimal homeomorphism inside
$\text{Homeo}(X)$. We point out that the full group of a minimal homeomorphism is topologically simple. We also study some properties of the closure of the full group of a minimal homeomorphism inside 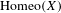 $\text{Homeo}(X)$.
$\text{Homeo}(X)$.