Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-28T10:43:18.195Z Has data issue: false hasContentIssue false
  • English
  • Français

A Franks’ lemma that preserves invariant manifolds

Published online by Cambridge University Press:  15 December 2014

NIKOLAZ GOURMELON
NIKOLAZ GOURMELON*
Affiliation:
Institut de Mathématiques de Bordeaux, Université Bordeaux 1, 351, cours de la Libération, F-33405 Talence cedex, France email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

D’après un célèbre lemme de John Franks, toute perturbation de la différentielle d’un difféomorphisme 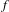$f$ le long d’une orbite périodique est réalisée par une 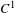$C^{1}$-perturbation $g$ du difféomorphisme sur un petit voisinage de ladite orbite. On n’a cependant aucune information sur le comportement des variétés invariantes de l’orbite périodique après perturbation. Nous montrons que si la perturbation de la dérivée est obtenue par une isotopie le long de laquelle existent les variétés stables/instables fortes de certaines dimensions, alors on peut faire la perturbation ci-dessus en préservant les variétés stables/instables semi-locales correspondantes. Ce résultat a de nombreuses applications en systèmes dynamiques de classes 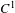$C^{1}$. Nous en démontrons quelques unes.

A well-known lemma by John Franks asserts that one obtains any perturbation of the derivative of a diffeomorphism along a periodic orbit by a 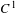$C^{1}$-perturbation of the whole diffeomorphism on a small neighbourhood of the orbit. However, one does not control where the invariant manifolds of the orbit are, after perturbation. We show that if the perturbed derivative is obtained by an isotopy along which some strong stable/unstable manifolds of some dimensions exist, then the Franks’ perturbation can be done preserving the corresponding stable/unstable semi-local manifolds. This is a general perturbative tool in 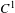$C^{1}$-dynamics that has many consequences. We give simple examples of such consequences, for instance a generic dichotomy between dominated splitting and small stable/unstable angles inside homoclinic classes.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 36 , Issue 4 , June 2016 , pp. 1167 - 1203
Copyright
© Cambridge University Press, 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arnaud, M.-C.. Création de connexions en topologie C 1. Ergod. Th. & Dynam. Sys. 21 (2001), 339–381.Google Scholar
Bochi, J. and Bonatti, C.. Perturbation of the Lyapunov spectra of periodic orbits. Proc. Lond. Math. Soc. (3) 105(1) (2012), 1–48, http://plms.oxfordjournals.org/content/105/1/1.Google Scholar
Bonatti, C. and Crovisier, S.. Récurrence et généricité. Invent. Math. 158 (2004), 33–104.CrossRefGoogle Scholar
Bonatti, C., Crovisier, S., Díaz, L. and Gourmelon, N.. Internal perturbations of homoclinic classes: non-domination, cycles, and self-replication. Ergod. Th. & Dynam. Sys. 33 (2013), 739–776.Google Scholar
Bonatti, C., Crovisier, S. and Shinohara, K.. The $C^{1+{\it\alpha}}$ hypothesis in Pesin theory revisited. Preprint, 2013, arXiv:1306.6391.CrossRefGoogle Scholar
Bonatti, Ch. and Díaz, L. J.. On maximal transitive sets of generic diffeomorphisms. Publ. Math. Inst. Hautes Études Sci. 96 (2002), 171–197.Google Scholar
Bonatti, C., Diaz, L. J. and Pujals, E. R.. A C 1 -generic dichotomy for diffeomorphisms: weak forms of hyperbolicity or infinitely many sinks or sources. Ann. of Math. (2) 158 (2000), 355–418.Google Scholar
Bonatti, C., Diaz, L. J. and Viana, M.. Dynamics Beyond Uniform Hyperbolicity. Springer, Berlin, 2005.Google Scholar
Bonatti, C., Gourmelon, N. and Vivier, T.. Perturbations of the derivative along periodic orbits. Ergod. Th. & Dynam. Sys. 26 (2006), 1307–1337.CrossRefGoogle Scholar
Bonatti, C., Li, M. and Yang, D.. On the existence of attractors. Preprint, 2009, arXiv:0904.4393.Google Scholar
Crovisier, S.. Periodic orbits and chain transitive sets of C 1 -diffeomorphisms. Publ. Math. Inst. Hautes Études Sci. 104 (2006), 87–141.Google Scholar
Franks, J.. Necessary conditions for stability of diffeomorphisms. Trans. Amer. Math. Soc. 158 (1971), 302–304.Google Scholar
Gourmelon, N.. Generation of homoclinic tangencies by C 1 -perturbations. Discrete Contin. Dyn. Syst. 26 (2010), 1–42.Google Scholar
Hayashi, S.. Connecting invariant manifolds and the solution of the C 1 -stability and Ω-stability conjectures for flows. Ann. of Math. (2) 145 (2000), 81–137.Google Scholar
Hirsch, M. W.. Differential Topology. Springer, New York, 1976.CrossRefGoogle Scholar
Katok, A. and Hasselblatt, B.. Modern Theory of Dynamical Systems. Cambridge University Press, 1995.Google Scholar
Mañé, R.. An ergodic closing lemma. Ann. of Math. (2) 116 (1982), 503–540.Google Scholar
Potrie, R.. Generic bi-Lyapunov stable homoclinic classes. Nonlinearity 23(7) (2010), 1631–1649.Google Scholar
Pugh, C.. The closing lemma. Amer. J. Math. 89 (1967), 956–1009.Google Scholar
Pugh, C.. The C 1+𝛼 hypothesis in Pesin theory. Publ. Math. Inst. Hautes Études Sci. 59 (1984), 143–161.Google Scholar
Pujals, E. R. and Sambarino, M.. Homoclinic tangencies and hyperbolicity for surface diffeomorphisms. Ann. of Math. (2) 151 (2000), 961–1023.Google Scholar
Wen, L.. Homoclinic tangencies and dominated splittings. Nonlinearity 15 (2002), 1445–1469.Google Scholar
Wen, L. and Xia, Z.. C 1 connecting lemmas. Trans. Amer. Math. Soc. 352(11) (2000), 5213–5230.Google Scholar
Yang, J.. Lyapunov stable chain-recurrent classes. Preprint, 2007, arXiv:0712.0514v1.Google Scholar