Hostname: page-component-6bf8c574d5-xtvcr Total loading time: 0 Render date: 2025-02-17T18:30:31.186Z Has data issue: false hasContentIssue false
  • English
  • Français

Formal classification of unfoldings of parabolic diffeomorphisms

Published online by Cambridge University Press:  01 August 2008

JAVIER RIBÓN
JAVIER RIBÓN*
Affiliation:
Departamento de Análise, Universidad Federal Fluminense, R. Mário Santos Braga, s/n, Niterói, RJ, Brasil (email: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We provide a complete system of invariants for the formal classification of unfoldings φ(x,x1,…,xn)=(f(x,x1,…,xn),x1,…,xn) of complex analytic germs of diffeomorphisms at 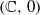that are tangent to the identity. We reduce the formal classification problem to solving a linear differential equation. Then we describe the formal invariants; their nature depends on the position of the fixed points set Fix φ with respect to the regular vector field ∂/∂x. We get invariants specifically attached to higher dimension (n≥3), although generically they are analogous to the one-dimensional ones.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 28 , Issue 4 , August 2008 , pp. 1323 - 1365
Copyright
Copyright © 2008 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Artin, M.. On the solutions of analytic equations. Invent. Math. 5 (1968), 277–291.Google Scholar
[2]Atiyah, M. F. and MacDonald, I. G.. Introduction to Commutative Algebra. Addison-Wesley, Reading, MA, 1969.Google Scholar
[3]Bruno, A. D.. Analytic form of differential equations. Trudy Moskov. Mat. Obshch. 25 (1971), 119–262; 26 (1972), 199–239Google Scholar
[4]Camacho, C.. On the local structure of conformal mappings and holomorphic vector fields in . Astérisque 59–60 (1978), 83–94.Google Scholar
[5]Gunning, R. C.. Introduction to Holomorphic Functions of Several Variables, Vol. II. Brooks/Cole, Monterey, CA, 1990.Google Scholar
[6]Elizarov, P. M., Il’yashenko, Yu. S., Scherbakov, A. A., Voronin, S. M. and Yakovenko, S. Yu.. Nonlinear Stokes Phenomena (Advances in Soviet Mathematics, 14). Ed. Yu. S. Il’yashenko. American Mathematical Society, Providence, RI, 1992.Google Scholar
[7]Kostov, V. P.. Versal deformations of differential forms of degree α on the line. Funktsional. Anal. i Prilozhen. 18(4) (1984), 81–82.Google Scholar
[8]Leau, L.. Étude sur les équations functionelles à une ou plusieurs variables. Ann. Fac. Sci. Toulouse 11 (1897).CrossRefGoogle Scholar
[9]Malgrange, B.. Travaux d’Écalle et de Martinet–Ramis sur les systèmes dynamiques. Astérisque 92–93 (1982), 59–73.Google Scholar
[10]Mardesic, P., Roussarie, R. and Rousseau, C.. Modulus of analytic classification of unfoldings of generic parabolic diffeomorphisms. Mosc. Math. J. 4(2) (2004), 455–502.Google Scholar
[11]Martinet, J. and Ramis, J.-P.. Classification analytique des équations différentielles non linéaires résonnantes du premier ordre. Ann. Sci. École Norm. Sup. (4) 16 (1983), 571–621.Google Scholar
[12]Martinet, J.. Remarques sur la bifurcation noeud-col dans le domaine complexe. Singularités d’Équations Différentielles (Dijon 1985). Astérisque 150–151 (1987), 131–149.Google Scholar
[13]Pérez-Marco, R.. Fixed points and circle maps. Acta Math. (2) 179 (1997), 243–294.Google Scholar
[14]Ribón, J.. Topological classification of families of diffeomorphisms without small divisors. Mem. Amer. Math. Soc. to appear.Google Scholar
[15]Ribón, J.. Modulus of analytic classification for unfoldings of resonant diffeomorphisms. Mosc. Math. J. to appear.Google Scholar
[16]Roussarie, R.. Modèles locaux de champs et de formes. Astérisque 30 (1975), 181.Google Scholar
[17]Scheja, G.. Riemannsche hebbarkeitssätze für cohomologieklassen. Math. Ann. 144 (1961), 345–360.Google Scholar
[18]Siegel, C. L.. Iterations of analytic functions. Ann. of Math. 43 (1942), 807–812.Google Scholar
[19]Voronin, S. M.. Analytical classification of germs of conformal mappings with identity linear part. Funct. Anal. Appl. 1(15) (1981), 1–17.Google Scholar
[20]Yoccoz, J.-C.. Théorème de Siegel, polynômes quadratiques et nombres de Brjuno. Astérisque 231 (1995), 3–88.Google Scholar