Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-26T01:11:13.319Z Has data issue: false hasContentIssue false
  • English
  • Français

Finite entropy for multidimensional cellular automata

Published online by Cambridge University Press:  01 August 2008

TOM MEYEROVITCH
TOM MEYEROVITCH*
Affiliation:
School of Mathematical Sciences, Tel-Aviv University, Ramat-Aviv, Tel-Aviv 69978, Israel (email: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 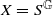where 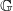is a countable group and S is a finite set. A cellular automaton (CA) is an endomorphism T:X→X (continuous, commuting with the action of 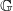). Shereshevsky [Expansiveness, entropy and polynomial growth for groups acting on subshifts by automorphisms. Indag. Math. (N.S.)4(2) (1993), 203–210] proved that for with d>1 no CA can be forward expansive, raising the following conjecture: for 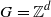, d>1, the topological entropy of any CA is either zero or infinite. Morris and Ward [Entropy bounds for endomorphisms commuting with K actions. Israel J. Math. 106 (1998), 1–11] proved this for linear CAs, leaving the original conjecture open. We show that this conjecture is false, proving that for any d there exists a d-dimensional CA with finite, non-zero topological entropy. We also discuss a measure-theoretic counterpart of this question for measure-preserving CAs.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 28 , Issue 4 , August 2008 , pp. 1243 - 1260
Copyright
Copyright © 2008 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Alber, J. and Niedermeier, R.. On multidimensional curves with Hilbert property. Theory Comput. Syst. 33(4) (2000), 295–312.CrossRefGoogle Scholar
[2]Bandini, S., Mauri, G. and Serra, R.. Cellular automata: from a theoretical parallel computational model to its application to complex systems. Parallel Comput. 27(5) (2001), 539–553 (Cellular Automata: From Modeling to Applications (Trieste, 1998)).CrossRefGoogle Scholar
[3]Blanchard, F., Kurka, P. and Maass, A.. Topological and measure-theoretic properties of one-dimensional cellular automata. Phys. D 103(1–4) (1997), 86–99 (Lattice Dynamics (Paris, 1995)).Google Scholar
[4]D’amico, M., Manzini, G. and Margara, L.. On computing the entropy of cellular automata. Theoret. Comput. Sci. 290(3) (2003), 1629–1646.Google Scholar
[5]Denker, M., Grillenberger, C. and Sigmund, K.. Ergodic Theory on Compact Spaces (Lecture Notes in Mathematics, 527). Springer, Berlin, 1976.CrossRefGoogle Scholar
[6]Goodman-Strauss, C.. Matching rules and substitution tilings. Ann. of Math. (2) 147(1) (1998), 181–223.CrossRefGoogle Scholar
[7]Hedlund, G. A.. Endormorphisms and automorphisms of the shift dynamical system. Math. Systems Theory 3 (1969), 320–375.Google Scholar
[8]Kari, J.. Reversibility and surjectivity problems of cellular automata. J. Comput. System Sci. 48(1) (1994), 149–182.CrossRefGoogle Scholar
[9]Kari, J.. Theory of cellular automata: A survey. Theoret. Comput. Sci. 334(1–3) (2005), 3–33.Google Scholar
[10]Lakshtanov, E. L. and Langvagen, E. S.. A criterion for the infinity of the topological entropy of multidimensional cellular automata. Problemy Peredachi Informatsii 40(2) (2004), 70–72.Google Scholar
[11]Morris, G. and Ward, T.. Entropy bounds for endomorphisms commuting with K actions. Israel J. Math. 106 (1998), 1–11.Google Scholar
[12]Mozes, S.. Tilings, substitution systems and dynamical systems generated by them. J. Anal. Math. 53 (1989), 139–186.Google Scholar
[13]Robinson, R. M.. Undecidability and nonperiodicity for tilings of the plane. Invent. Math. 12 (1971), 177–209.CrossRefGoogle Scholar
[14]Shereshevsky, M. A.. Expansiveness, entropy and polynomial growth for groups acting on subshifts by automorphisms. Indag. Math. (N.S.) 4(2) (1993), 203–210.Google Scholar
[15]von Neumann, J.. Theory of Self-Reproducing Automata. University of Illinois Press, Urbana, IL, 1966.Google Scholar
[16]Wolfram, S.. A New Kind of Science. Wolfram Media, Inc., Champaign, IL, 2002.Google Scholar