Published online by Cambridge University Press: 23 April 2014
We study invariant Fatou components for holomorphic endomorphisms in 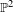 $\mathbb{P}^{2}$. In the recurrent case these components were classified by Fornæss and Sibony [Classification of recurrent domains for some holomorphic maps. Math. Ann. 301(4) (1995), 813–820]. Ueda [Holomorphic maps on projective spaces and continuations of Fatou maps. Michigan Math J.56(1) (2008), 145–153] completed this classification by proving that it is not possible for the limit set to be a punctured disk. Recently Lyubich and Peters [Classification of invariant Fatou components for dissipative Hénon maps. Preprint] classified non-recurrent invariant Fatou components, under the additional hypothesis that the limit set is unique. Again all possibilities in this classification were known to occur, except for the punctured disk. Here we show that the punctured disk can indeed occur as the limit set of a non-recurrent Fatou component. We provide many additional examples of holomorphic and polynomial endomorphisms of
$\mathbb{P}^{2}$. In the recurrent case these components were classified by Fornæss and Sibony [Classification of recurrent domains for some holomorphic maps. Math. Ann. 301(4) (1995), 813–820]. Ueda [Holomorphic maps on projective spaces and continuations of Fatou maps. Michigan Math J.56(1) (2008), 145–153] completed this classification by proving that it is not possible for the limit set to be a punctured disk. Recently Lyubich and Peters [Classification of invariant Fatou components for dissipative Hénon maps. Preprint] classified non-recurrent invariant Fatou components, under the additional hypothesis that the limit set is unique. Again all possibilities in this classification were known to occur, except for the punctured disk. Here we show that the punctured disk can indeed occur as the limit set of a non-recurrent Fatou component. We provide many additional examples of holomorphic and polynomial endomorphisms of 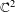 $\mathbb{C}^{2}$ with non-recurrent Fatou components on which the orbits converge to the regular part of arbitrary analytic sets.
$\mathbb{C}^{2}$ with non-recurrent Fatou components on which the orbits converge to the regular part of arbitrary analytic sets.