Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-24T17:00:26.154Z Has data issue: false hasContentIssue false
  • English
  • Français

A family of entire functions with Baker domains

Published online by Cambridge University Press:  01 April 2009

DOMINIQUE S. FLEISCHMANN
DOMINIQUE S. FLEISCHMANN*
Affiliation:
Department of Mathematics and Statistics, The Open University, Walton Hall, Milton Keynes MK7 6AA, UK (email: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

In his paper [The iteration of polynomials and transcendental entire functions. J. Aust. Math. Soc. (Series A)30 (1981), 483–495], Baker proved that the function f defined by 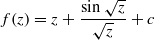has a Baker domain for c sufficiently large. In this paper we use a novel method to prove that f has a Baker domain for all c>0. We also prove that there exists an open unbounded set contained in the Baker domain on which the orbits of points under f are asymptotically horizontal.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 29 , Issue 2 , April 2009 , pp. 495 - 514
Copyright
Copyright © Cambridge University Press 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Baker, I. N.. The iteration of polynomials and transcendental entire functions. J. Aust. Math. Soc. (Series A) 30 (1981), 483–495.CrossRefGoogle Scholar
[2]Beardon, A. F.. Iteration of Rational Functions. Springer, Berlin, 1991.CrossRefGoogle Scholar
[3]Bergweiler, W.. Iteration of meromorphic functions. Bull. Amer. Math. Soc. 29 (1993), 151–188.CrossRefGoogle Scholar
[4]Fleischmann, D. S.. An entire function with a Baker domain and sparsely distributed singular values. Math. Proc. Cambridge Philos. Soc. 145 (2008), 227–241.CrossRefGoogle Scholar
[5]Morosawa, S.. An example of cyclic Baker domains. Mem. Fac. Sci. Kochi Univ. Ser. A Math. 20 (1999), 123–126.Google Scholar
[6]Morosawa, S., Nishimura, Y., Taniguchi, M. and Ueda, T.. Holomorphic Dynamics (Cambridge Studies in Advanced Mathematics, 66). Cambridge University Press, Cambridge, 1999.Google Scholar
[7]Rippon, P. J.. Baker domains. Transcendental Dynamics and Complex Analysis (Lecture Notes in Mathematics, 348). Cambridge University Press, Cambridge, 2008, pp. 371–395.CrossRefGoogle Scholar