Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-26T00:45:21.952Z Has data issue: false hasContentIssue false
  • English
  • Français

Extensive bounds on the topological entropy of repellers in piecewise expanding coupled map lattices

Published online by Cambridge University Press:  17 April 2012

RICARDO COUTINHO  and
BASTIEN FERNANDEZ
RICARDO COUTINHO
Affiliation:
Grupo de Física Matemática, Universidade de Lisboa, 1649-003 Lisboa, Portugal Departamento de Matemática, Instituto Superior Técnico, Universidade Técnica de Lisboa, 1049-001 Lisboa, Portugal (email: [email protected])
BASTIEN FERNANDEZ
Affiliation:
Centre de Physique Théorique, UMR 7332 CNRS – Aix-Marseille Université, Campus de Luminy, 13288 Marseille CEDEX 9, France (email: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Beyond the uncoupled regime, the rigorous description of the dynamics of (piecewise) expanding coupled map lattices remains largely incomplete. To address this issue, we study repellers of periodic chains of linearly coupled Lorenz-type maps which we analyze by means of symbolic dynamics. Whereas all symbolic codes are admissible for sufficiently small coupling intensity, when the interaction strength exceeds a chain length independent threshold, we prove that a large bunch of codes is pruned and an extensive decay follows suit for the topological entropy. This quantity, however, does not immediately drop off to 0. Instead, it is shown to be continuous at the threshold and to remain extensively bounded below by a positive number in a large part of the expanding regime. The analysis is firstly accomplished in a piecewise affine setting where all calculations are explicit and is then extended by continuation to coupled map lattices based on 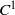$C^1$-perturbations of the individual map.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 33 , Issue 3 , June 2013 , pp. 870 - 895
Copyright
Copyright © 2012 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Afraimovich, V. and Fernandez, B.. Topological properties of linearly coupled expanding map lattices. Nonlinearity 13 (2000), 973–993.Google Scholar
[2]Bardet, J.-B. and Fernandez, B.. Extensive escape rate in lattices of weakly coupled expanding maps. Discrete Contin. Dyn. Syst. A 31 (2011), 669–684.CrossRefGoogle Scholar
[3]Bardet, J.-B. and Keller, G.. Phase transitions in a piecewise expanding coupled map lattice with linear nearest neighbour coupling. Nonlinearity 19 (2006), 2193–2210.Google Scholar
[4]Bricmont, J. and Kupiainen, A.. Coupled analytic maps. Phys. D 8 (1995), 379–396.Google Scholar
[5]Bunimovich, L. and Sinai, Y.. Space–time chaos in coupled map lattices. Nonlinearity 1 (1988), 491–516.Google Scholar
[6]Chazottes, J.-R. and Fernandez, B. (eds) Dynamics of Coupled Map Lattices and of Related Spatially Extended Systems (Lecture Notes in Physics, 671). Springer, Berlin, 2005.Google Scholar
[7]Coutinho, R., Fernandez, B. and Guiraud, P.. Symbolic dynamics of two coupled Lorenz maps: from uncoupled regime to synchronisation. Phys. D 237 (2008), 2444–2462.Google Scholar
[8]Falconer, K.. Fractal Geometry: Mathematical Foundations and Applications, 2nd edn. Wiley, Chichester, 2003.Google Scholar
[9]Fernandez, B.. Global synchronisation in translation invariant coupled map lattices. Internat. J. Bifur. Chaos 18 (2008), 3455–3459.Google Scholar
[10]Fernandez, B. and Guiraud, P.. Route to chaotic synchronisation in coupled map lattices: rigorous results. Discrete Contin. Dyn. Syst. B 4 (2004), 435–455.Google Scholar
[11]Fernandez, B. and Jiang, M.. Coupling two unimodal maps of simple kneading sequences. Ergod. Th. & Dynam. Sys. 24 (2004), 107–125.CrossRefGoogle Scholar
[12]Gielis, G. and MacKay, R.. Coupled map lattices with phase transitions. Nonlinearity 13 (2000), 867–888.CrossRefGoogle Scholar
[13]Guckenheimer, J. and Holmes, P.. Nonlinear Oscillators, Dynamical Systems and Bifurcations of Vector Fields. Springer, New York, 1983.CrossRefGoogle Scholar
[14]Jiang, M. and Pesin, Y.. Equilibrium measures for coupled map lattices: existence, uniqueness and finite-dimensional approximations. Comm. Math. Phys. 193 (1998), 675–711.Google Scholar
[15]Jost, J. and Joy, M.. Spectral properties and synchronization in coupled map lattices. Phys. Rev. E 65 (2001), 016201.CrossRefGoogle ScholarPubMed
[16]Kaneko, K.. Period-doubling of kink-antikink patterns, quasiperiodicity in antiferro-like structures and spatial intermittency in coupled logistic lattice. Progr. Theoret. Phys. 72 (1984), 480–486.CrossRefGoogle Scholar
[17]Kaneko, K. (ed.) Theory and Applications of Coupled Map Lattices. Wiley, Chichester, 1993.Google Scholar
[18]Katok, A. and Hasselblatt, B.. Introduction to the Modern Theory of Dynamical Systems. Cambridge University Press, Cambridge, 1995.Google Scholar
[19]Keller, G., Künzle, M. and Nowicki, T.. Some phase transitions in coupled map lattices. Phys. D 59 (1992), 39–51.Google Scholar
[20]Keller, G. and Liverani, C.. Uniqueness of the SRB measure for piecewise expanding weakly coupled map lattices in any dimension. Comm. Math. Phys. 262 (2006), 33–50.Google Scholar
[21]Koiller, J. and Young, L.-S.. Coupled map networks. Nonlinearity 23 (2010), 1121–1141.Google Scholar
[22]Lind, D. and Marcus, B.. An Introduction to Symbolic Dynamics and Coding. Cambridge University Press, Cambridge, 1995.CrossRefGoogle Scholar
[23]Lind, P., Corte-Real, J. and Gallas, J.. Modeling velocity in gradient flows with coupled-map lattices with advection. Phys. Rev. E 66 (2002), 016219.Google Scholar
[24]MacKay, R.. Dynamics of networks: features which persist from the uncoupled limit. Stochastic and Spatial Structures of Dynamical Systems, Lunel (1996), 81–104.Google Scholar
[25]Oono, Y. and Puri, S.. Computationally efficient modeling of ordering of quenched phases. Phys. Rev. Lett. 58 (1987), 836–839.Google Scholar
[26]Rand, D.. The topological classification of Lorenz attractors. Math. Proc. Cambridge Philos. Soc. 83 (1978), 451–460.Google Scholar
[27]Robinson, C.. Dynamical Systems, 2nd edn. CRC Press, Boca Raton, FL, 1999.Google Scholar
[28]Solé, R., Valls, J. and Bascompte, J.. Spiral waves, chaos and multiple attractors in lattice models of interacting populations. Phys. Lett. A 166 (1992), 123–128.Google Scholar
[29]Waller, I. and Kapral, R.. Spatial and temporal structure in systems of coupled nonlinear oscillators. Phys. Rev. A 30 (1984), 2047–2055.Google Scholar