Published online by Cambridge University Press: 08 May 2012
In this paper, we show that the Hénon map 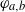 $\varphi _{a,b}$ has a generically unfolding cubic tangency for some
$\varphi _{a,b}$ has a generically unfolding cubic tangency for some 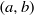 $(a,b)$ arbitrarily close to
$(a,b)$ arbitrarily close to 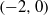 $(-2,0)$ by applying results of Gonchenko, Shilnikov and Turaev [On models with non-rough Poincaré homoclinic curves. Physica D 62(1–4) (1993), 1–14; Dynamical phenomena in systems with structurally unstable Poincaré homoclinic orbits. Chaos 6(1) (1996), 15–31; On Newhouse domains of two-dimensional diffeomorphisms which are close to a diffeomorphism with a structurally unstable heteroclinic cycle. Proc. Steklov Inst. Math.216 (1997), 70–118; Homoclinic tangencies of an arbitrary order in Newhouse domains. Itogi Nauki Tekh. Ser. Sovrem. Mat. Prilozh. 67 (1999), 69–128, translation in J. Math. Sci. 105 (2001), 1738–1778; Homoclinic tangencies of arbitrarily high orders in conservative and dissipative two-dimensional maps. Nonlinearity 20 (2007), 241–275]. Combining this fact with theorems in Kiriki and Soma [Persistent antimonotonic bifurcations and strange attractors for cubic homoclinic tangencies. Nonlinearity 21(5) (2008), 1105–1140], one can observe the new phenomena in the Hénon family, appearance of persistent antimonotonic tangencies and cubic polynomial-like strange attractors.
$(-2,0)$ by applying results of Gonchenko, Shilnikov and Turaev [On models with non-rough Poincaré homoclinic curves. Physica D 62(1–4) (1993), 1–14; Dynamical phenomena in systems with structurally unstable Poincaré homoclinic orbits. Chaos 6(1) (1996), 15–31; On Newhouse domains of two-dimensional diffeomorphisms which are close to a diffeomorphism with a structurally unstable heteroclinic cycle. Proc. Steklov Inst. Math.216 (1997), 70–118; Homoclinic tangencies of an arbitrary order in Newhouse domains. Itogi Nauki Tekh. Ser. Sovrem. Mat. Prilozh. 67 (1999), 69–128, translation in J. Math. Sci. 105 (2001), 1738–1778; Homoclinic tangencies of arbitrarily high orders in conservative and dissipative two-dimensional maps. Nonlinearity 20 (2007), 241–275]. Combining this fact with theorems in Kiriki and Soma [Persistent antimonotonic bifurcations and strange attractors for cubic homoclinic tangencies. Nonlinearity 21(5) (2008), 1105–1140], one can observe the new phenomena in the Hénon family, appearance of persistent antimonotonic tangencies and cubic polynomial-like strange attractors.