Article contents
Eventually positive matrices with rational eigenvectors†
Published online by Cambridge University Press: 19 September 2008
Abstract
Let A be an n × n real matrix; sufficient conditions were previously worked out, assuming non-commensurability of eigenvectors, for A to be SL(n, 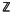 )-conjugate to a matrix all sufficiently large powers of which have strictly positive entries. We show that when the ‘large’ eigenvectors are commensurable and satisfy the obvious necessary conditions, then A is also going to be so conjugate. In particular, we deduce, if A is a rational matrix with large eigenvalue exceeding 1 and of multiplicity one, then A is algebraically shift equivalent to an eventually positive matrix, using only integer rectangular matrices.
)-conjugate to a matrix all sufficiently large powers of which have strictly positive entries. We show that when the ‘large’ eigenvectors are commensurable and satisfy the obvious necessary conditions, then A is also going to be so conjugate. In particular, we deduce, if A is a rational matrix with large eigenvalue exceeding 1 and of multiplicity one, then A is algebraically shift equivalent to an eventually positive matrix, using only integer rectangular matrices.
- Type
- Research Article
- Information
- Copyright
- Copyright © Cambridge University Press 1987
References
REFERENCE
- 9
- Cited by


