Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-24T01:02:13.639Z Has data issue: false hasContentIssue false
  • English
  • Français

The essential coexistence phenomenon in Hamiltonian dynamics

Part of: Dynamical systems with hyperbolic behavior Smooth dynamical systems: general theory

Published online by Cambridge University Press:  08 April 2021

JIANYU CHEN ,
HUYI HU ,
YAKOV PESIN  and
KE ZHANG
JIANYU CHEN
Affiliation:
School of Mathematical Sciences & Center for Dynamical Systems and Differential Equations, Soochow University, Suzhou215006, Jiangsu, P.R. China (e-mail: [email protected])
HUYI HU
Affiliation:
Department of Mathematics, Michigan State University, East Lansing, MI48824, USA (e-mail: [email protected])
YAKOV PESIN*
Affiliation:
Department of Mathematics, Pennsylvania State University, University Park, State College, PA16802, USA
KE ZHANG
Affiliation:
Department of Mathematics, University of Toronto, Toronto, Ontario, Canada (e-mail: [email protected])
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

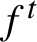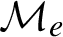We construct an example of a Hamiltonian flow $f^t$ on a four-dimensional smooth manifold $\mathcal {M}$ which after being restricted to an energy surface $\mathcal {M}_e$ demonstrates essential coexistence of regular and chaotic dynamics, that is, there is an open and dense 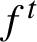$f^t$ -invariant subset 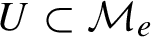$U\subset \mathcal {M}_e$ such that the restriction 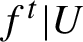$f^t|U$ has non-zero Lyapunov exponents in all directions (except for the direction of the flow) and is a Bernoulli flow while, on the boundary 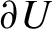$\partial U$ , which has positive volume, all Lyapunov exponents of the system are zero.

Keywords

essential coexistenceHamiltonian flowsLyapunov exponentsBernoulli maps

MSC classification

Primary: 37D35: Thermodynamic formalism, variational principles, equilibrium states 37C45: Dimension theory of dynamical systems
Secondary: 37C40: Smooth ergodic theory, invariant measures 37D20: Uniformly hyperbolic systems (expanding, Anosov, Axiom A, etc.)
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 42 , Issue 2: Anatole Katok Memorial Issue Part 1: Special Issue of Ergodic Theory and Dynamical Systems , February 2022 , pp. 592 - 613
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Dedicated to the memory of Anatole Katok

References

Arnold, V. I., Kozlov, V. V. and Neishtadt, A. I.. Mathematical Aspects of Classical and Celestial Mechanics (Dynamical Systems III, Encyclopaedia of Mathematical Sciences, 3), 3rd edn. Springer, Berlin, 2006. Translated from the Russian original by E. Khukhro.Google Scholar
Berger, P. and Turaev, D.. On Herman’s positive entropy conjecture. Adv. Math. 349 (2019), 1234–1288.CrossRefGoogle Scholar
Chen, J.. On essential coexistence of zero and nonzero Lyapunov exponents. Discrete Contin. Dyn. Syst. 32 (2012), 4149–4170.10.3934/dcds.2012.32.4149CrossRefGoogle Scholar
Chen, J., Hu, H. and Pesin, Y.. The essential coexistence phenomenon in dynamics. Dyn. Syst. 28 (2013), 453–472.CrossRefGoogle Scholar
Chen, J., Hu, H. and Pesin, Y.. A volume preserving flow with essential coexistence of zero and non-zero Lyapunov exponents. Ergod. Th. & Dynam. Sys. 33 (2013), 1748–1785.Google Scholar
Cheng, C.-Q. and Sun, Y.-S.. Existence of invariant tori in three dimensional measure-preserving mappings. Celestial Mech. Dynam. Astronom. 47 (1990), 275–292.CrossRefGoogle Scholar
Fisher, T. and Hasselblatt, B.. Hyperbolic Flows (Zurich Lectures in Advanced Mathematics). European Mathematical Society, Zurich, 2020.Google Scholar
Guillemin, V. and Pollack, A.. Differential Topology. Prentice-Hall, Englewood Cliffs, NJ, 1974, p. 222.Google Scholar
Greene, R. E. and Shiohama, K.. Diffeomorphisms and volume-preserving embeddings of noncompact manifolds. Trans. Amer. Math. Soc. 255 (1979), 403–414.CrossRefGoogle Scholar
Herman, M.. Stabilité topologique des systémes dynamiques conservatifs. Proc. 18th Brazilian Colloquium on Mathematics (in Portuguese), 1992, Twist Mappings and Their Applications. Springer, New York, 1992, pp. 153–182.Google Scholar
Hu, H., Pesin, Y. and Talitskaya, A.. Every compact manifold carries a hyperbolic Bernoulli flow. Modern Dynamical Systems and Applications. Cambridge University Press, Cambridge, 2004, pp. 347–358.Google Scholar
Hu, H., Pesin, Y. and Talitskaya, A.. A volume preserving diffeomorphism with essential coexistence of zero and nonzero Lyapunov exponents. Comm. Math. Phys. 319 (2013), 331–378.CrossRefGoogle Scholar
Katok, A.. Bernoulli diffeomorphisms on surfaces. Ann. of Math. (2) 110(3) (1979), 529–547.CrossRefGoogle Scholar
Munkres, J. Analysis on Manifolds. Addison-Wesley, Advanced Book Program, Redwood City, CA, 1991, p. 366.Google Scholar
Xia, J.. Existence of invariant tori in volume-preserving diffeomorphisms. Ergod. Th. & Dynam. Sys. 12 (1992), 275–292.CrossRefGoogle Scholar
Yoccoz, J.-C.. Travaux de Herman sur les tores invariants. Astérisque 206 (1992), 311–344.Google Scholar