Hostname: page-component-6bf8c574d5-9nwgx Total loading time: 0 Render date: 2025-02-17T01:13:34.776Z Has data issue: false hasContentIssue false
  • English
  • Français

Escape components of McMullen maps

Part of: Complex dynamical systems

Published online by Cambridge University Press:  28 November 2022

WEIYUAN QIU ,
PASCALE ROESCH  and
YUEYANG WANG
WEIYUAN QIU
Affiliation:
School of Mathematical Sciences, Fudan University, Shanghai, 200433, P. R. China (e-mail: [email protected])
PASCALE ROESCH
Affiliation:
IMT, Laboratoire Emile Picard, Université Paul Sabatier, 118, route de Narbonne, 31062 Toulouse Cedex 9, France (e-mail: [email protected])
YUEYANG WANG*
Affiliation:
Department of Mathematics Zhejiang University, Hangzhou, 310027, P. R. China
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider the McMullen maps 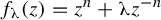$f_{\unicode{x3bb} }(z)=z^{n}+\unicode{x3bb} z^{-n}$ with 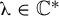$\unicode{x3bb} \in \mathbb {C}^{*}$ and 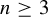$n \geq 3$. We prove that the closures of escape hyperbolic components are pairwise disjoint and the boundaries of all bounded escape components (the McMullen domain and Sierpiński holes) are quasi-circles with Hausdorff dimension strictly between 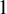$1$ and 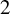$2$.

Keywords

hyperbolic componentMcMullen mapquasicircleholomorphic motion

MSC classification

Primary: 37F45: Holomorphic families of dynamical systems; the Mandelbrot set; bifurcations
Secondary: 37F10: Polynomials; rational maps; entire and meromorphic functions 37F15: Expanding maps; hyperbolicity; structural stability
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 43 , Issue 11 , November 2023 , pp. 3745 - 3775
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

*

The original version of this article contained an error in the name Pascale Roesch. This error has been corrected. A notice detailing this error has been published.

References

Ahlfors, L. V.. Lectures on Quasiconformal Mappings (University Lecture Series, 38). American Mathematical Society, Toronto, 2006.10.1090/ulect/038CrossRefGoogle Scholar
Avila, A., Lyubich, M. and Shen, W.. Parapuzzle of the multibrot set and typical dynamics of unimodal maps. J. Eur. Math. Soc. (JEMS) 13(1) (2010), 27–56.Google Scholar
Astala, K.. Area distortion of quasiconformal mappings. Acta Math. 173 (1994), 37–60.10.1007/BF02392568CrossRefGoogle Scholar
Blanchard, P., Devaney, R. L., Look, D. M., Seal, P. and Shapiro, Y.. Sierpinski-curve Julia sets and singular perturbations of complex polynomials. Ergod. Th. & Dynam. Sys. 25(4):1047–1055, 2005.10.1017/S0143385704000380CrossRefGoogle Scholar
Branner, B. and Hubbard, J. H.. The iteration of cubic polynomials part II: patterns and parapatterns. Acta Math. 169(1) (1992), 229–325.10.1007/BF02392761CrossRefGoogle Scholar
Devaney, R. L.. Cantor necklaces and structurally unstable Sierpinski curve Julia sets for rational maps. Qual. Theory Dyn. Syst. 5(2) (2004), 337.10.1007/BF02972685CrossRefGoogle Scholar
Devaney, R. L.. Structure of the McMullen domain in the parameter planes for rational maps. Fund. Math. 185 (2005), 267–285.10.4064/fm185-3-5CrossRefGoogle Scholar
Devaney, R. L.. Baby Mandelbrot sets adorned with halos in families of rational maps. Complex Dynamics (Contemporary Mathematics, 396). American Mathematical Society, Providence, RI, 2006, pp. 37–50.10.1090/conm/396/07392CrossRefGoogle Scholar
Devaney, R. L.. The McMullen domain: satellite Mandelbrot sets and Sierpinski holes. Conform. Geom. Dyn. 11(12) (2007), 164–190.10.1090/S1088-4173-07-00166-XCrossRefGoogle Scholar
Devaney, R. L.. Cantor webs in the parameter and dynamical planes of rational maps. Holomorphic Dynamics and Renormalization. (Fields Institute Communications). Eds. Lyubich, M. and Yampolsky, M.. American Mathematical Society, Providence, RI, 2008, pp. 105–123.10.1090/fic/053/05CrossRefGoogle Scholar
Devaney, R. L.. Singular perturbations of complex polynomials. Bull. Amer. Math. Soc. (N.S.) 50(3) (2013), 391–429.10.1090/S0273-0979-2013-01410-1CrossRefGoogle Scholar
Douady, A. and Hubbard, J. H.. A proof of Thurston’s topological characterization of rational functions. Acta Math. 171(2) (1993), 263–297.10.1007/BF02392534CrossRefGoogle Scholar
Douady, A. and Hubbard, J.. Étude dynamique des polynômes complexes, I, II (Publications Mathématiques d'Orsay, 84-02 and 85-04). Université de Paris-Sud, Dép. de Mathématique, Orsay, France, 1984.Google Scholar
Devaney, R. L. and Look, D. M.. Symbolic dynamics for a Sierpinski curve Julia set. J. Difference Equ. Appl. 11(7) (2005), 581–596.10.1080/10236190412331334473CrossRefGoogle Scholar
Devaney, R. L., Look, D. M. and Uminsky, D.. The escape trichotomy for singularly perturbed rational maps. Indiana Univ. Math. J. 54 (2005), 1621–1634.10.1512/iumj.2005.54.2615CrossRefGoogle Scholar
Devaney, R. L. and Marotta, S.. The McMullen domain: rings around the boundary. Trans. Amer. Math. Soc. 359(7) (2007), 3251–3273.10.1090/S0002-9947-07-04137-2CrossRefGoogle Scholar
Douady, A.. Prolongement de mouvements holomorphes. Astérisque 227(1) (1995), 1–12.Google Scholar
Devaney, R. L. and Pilgrim, K.. Dynamic classification of escape time Sierpiński curve Julia sets. Fund. Math. 2(202) (2009), 181–198.10.4064/fm202-2-5CrossRefGoogle Scholar
Falconer, K.. Fractal Geometry: Mathematical Foundations and Applications. John Wiley & Sons, Chichester, 2004.Google Scholar
Faught, D.. Local connectivity in a family of cubic polynomials. PhD Thesis, Cornell University, 1993.Google Scholar
Hubbard, J. H.. Local Connectivity of Julia Sets and Bifurcation Loci: Three Theorems of J.-C. Yoccoz (Topological Methods in Modern Mathematics, Proceedings of a Symposium in Honor of John Milnor's Sixtieth Birthday). Eds. Goldberg, L. and Phillips, A.. Publish or Perish, Houston, TX, 1993, pp. 467–511.Google Scholar
Hubbard, J. H.. Teichmüller Theory and Applications to Geometry, Topology, and Dynamics, Volume I: Teichmüller Theory. Matrix Editions, New York, 2006.Google Scholar
Kahn, J. and Lyubich, M.. Local connectivity of Julia sets for unicritical polynomials. Ann. of Math. (2) 170 (2009), 413–426.10.4007/annals.2009.170.413CrossRefGoogle Scholar
Kozlovski, O., Shen, W. and van Strien, S.. Rigidity for real polynomials. Ann. of Math. (2) 165 (2007), 749–841.10.4007/annals.2007.165.749CrossRefGoogle Scholar
Lavaurs, P.. Systemes dynamiques holomorphes: explosion de points périodiques paraboliques. PhD Thesis, Paris 11, 1989.Google Scholar
Lei, T.. Local properties of the Mandelbrot set at parabolic points. The Mandelbrot Set, Theme and Variations (London Mathematical Society Lecture Notes Series, 274). Ed. Lei, T.. Cambridge University Press, Cambridge, 2000, pp. 133–160.10.1017/CBO9780511569159.008CrossRefGoogle Scholar
Levin, G. and van Strien, S.. Local connectivity of the Julia set of real polynomials. Ann. of Math. (2) 147 (1998), 471–541.10.2307/120958CrossRefGoogle Scholar
Lyubich, M.. Dynamics of quadratic polynomials, III Parapuzzle and SBR measures. Astérisque 261 (2000), 173–200.Google Scholar
McMullen, C.. Automorphisms of rational maps. Holomorphic Functions and Moduli I. Eds. Drasin, D., Kra, I., Earle, C. J., Marden, A. and Gehring, F. W.. Springer, Berlin, 1988, pp. 31–60.10.1007/978-1-4613-9602-4_3CrossRefGoogle Scholar
Milnor, J.. Dynamics in One Complex Variable (Annals of Mathematical Studies, AM-160), Vol. 197. Ed. Milnor, J.. Princeton University Press, Princeton, NJ, 2011.Google Scholar
Petersen, C. L.. Local connectivity of some Julia sets containing a circle with an irrational rotation. Acta Math. 177(2) (1996), 163–224.10.1007/BF02392621CrossRefGoogle Scholar
Przytycki, F.. On the hyperbolic Hausdorff dimension of the boundary of a basin of attraction for a holomorphic map and of quasirepellers. Bull. Pol. Acad. Sci. Math. 54 (2006), 41–52.10.4064/ba54-1-4CrossRefGoogle Scholar
Qiu, W., Roesch, P., Wang, X. and Yin, Y.. Hyperbolic components of McMullen maps. Ann. Sci. Éc. Norm. Supér (4) 48(3) (2015), 703–737.10.24033/asens.2256CrossRefGoogle Scholar
Qiu, W., Wang, X. and Yin, Y.. Dynamics of McMullen maps. Adv. Math. 229 (2012), 2525–2577.10.1016/j.aim.2011.12.026CrossRefGoogle Scholar
Qiu, W. and Yin, Y.. Proof of the Branner–Hubbard conjecture on Cantor Julia sets. Sci. China Ser. A: Math. 52(1) (2009), 45.10.1007/s11425-008-0178-9CrossRefGoogle Scholar
Roesch, P.. Holomorphic motions and puzzles (following M. Shishikura). The Mandelbrot Set, Theme and Variations (London Mathematical Society Lecture Notes Series, 274). Ed. Lei, T.. Cambridge University Press, Cambridge, 2000, pp. 117–132.CrossRefGoogle Scholar
Roesch, P.. On capture zones for the family ${f}_c(z)={z}^2+c/ {z}^2$ . Dynamics on the Riemann Sphere, Eds. Lude Peterson, C. and Hjorth, P. G.. EMS Press, Berlin, 2006, pp. 121–129.10.4171/011-1/6CrossRefGoogle Scholar
Roesch, P.. Hyperbolic components of polynomials with a fixed critical point of maximal order. Ann. Sci. Éc. Norm. Supér (4) 40(6) (2007), 901–949.10.1016/j.ansens.2007.10.001CrossRefGoogle Scholar
Roesch, P.. On local connectivity for the Julia set of rational maps: Newton’s famous example. Ann. of Math. (2) 168(1) (2008), 127–174.10.4007/annals.2008.168.127CrossRefGoogle Scholar
Schleicher, D.. On fibers and local connectivity. Fractal Geometry and Applications: A Jubilee of Benoit Mandelbrot, (Proceedings of Symposia in Pure Mathematics, 72). Eds. Lapidus, M. and Frankenhuijsen, M. V.. American Mathematical Society, Providence, RI, 2004, pp. 477.10.1090/pspum/072.1/2112117CrossRefGoogle Scholar
Shishikura, M.. The Hausdorff dimension of the boundary of the Mandelbrot set and Julia sets. Ann. of Math. (2) 147 (1998), 225–267.10.2307/121009CrossRefGoogle Scholar
Shishikura, M.. Bifurcation of parabolic fixed points. The Mandelbrot Set, Theme and Variations (London Mathematical Society Lecture Notes Series Series, 274). Ed. Lei, T.. Cambridge University Press, Cambridge, 2000, pp. 325–364.10.1017/CBO9780511569159.018CrossRefGoogle Scholar
Slodkowski, Z.. Extensions of holomorphic motions. Ann. Sc. Norm. Super. Pisa Cl. Sci. (5) 22(2) (1995), 185–210.Google Scholar
Steinmetz, N.. On the dynamics of the McMullen family. Conform. Geom. Dyn. 10(09) (2006), 159–184.10.1090/S1088-4173-06-00149-4CrossRefGoogle Scholar