Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-26T00:30:06.181Z Has data issue: false hasContentIssue false
  • English
  • Français

Ergodic properties of 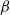$\beta $-adic Halton sequences

Published online by Cambridge University Press:  11 October 2013

MARKUS HOFER ,
MARIA RITA IACÒ  and
ROBERT TICHY
MARKUS HOFER
Affiliation:
Johannes Kepler University, Institute of Financial Mathematics, Altenbergerstrasse 69, 4040 Linz, Austria email [email protected]
MARIA RITA IACÒ
Affiliation:
Graz University of Technology, Institute of Mathematics A, Steyrergasse 30, 8010 Graz, Austria email [email protected]@tugraz.at University of Calabria, Department of Mathematics and Computer Science, Via P. Bucci 30B, 87036 Arcavacata di Rende (CS), Italy email [email protected]
ROBERT TICHY
Affiliation:
Graz University of Technology, Institute of Mathematics A, Steyrergasse 30, 8010 Graz, Austria email [email protected]@tugraz.at
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate a parametric extension of the classical $s$-dimensional Halton sequence where the bases are special Pisot numbers. In a one-dimensional setting the properties of such sequences have already been investigated by several authors. We use methods from ergodic theory in order to investigate the distribution behavior of multidimensional versions of such sequences. As a consequence it is shown that the Kakutani–Fibonacci transformation is uniquely ergodic.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 35 , Issue 3 , May 2015 , pp. 895 - 909
Copyright
© Cambridge University Press, 2013 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aistleitner, C., Hofer, M. and Ziegler, V.. On the uniform distribution modulo 1 of multidimensional LS-sequences. Ann. Mat. Pura Appl. (2013) to appear.CrossRefGoogle Scholar
Akiyama, S.. Cubic Pisot numbers with finite beta expansions. Algebraic Number Theory and Diophantine Analysis. Eds. Halter-Koch, F. and Tichy, R.. Walter de Gruyter, Berlin, 2000, pp. 11–26.Google Scholar
Akiyama, S., Brunotte, H., Pethö, A. and Thuswaldner, J. M.. Generalized radix representations and dynamical systems II. Acta Arith. 121 (2006), 21–61.Google Scholar
Asmussen, S. and Albrecher, H.. Ruin Probabilities, 2nd edn. World Scientific, Singapore, 2010.Google Scholar
Barat, G. and Grabner, P.. Distribution properties of $G$-additive functions. J. Number Theory 60 (1996), 103–123.Google Scholar
Bruin, H., Keller, G. and Pierre, M.. Adding machines and wild attractors. Ergod. Th. & Dynam. Sys. 17 (6) (1997), 1267–1287.Google Scholar
Carbone, I.. Discrepancy of LS-sequences of partitions and points. Ann. Mat. Pura Appl. (4) 191 (4) (2012), 819–844.Google Scholar
Carbone, I., Iacò, M. R. and Volčič, A.. A dynamical system approach to the Kakutani–Fibonacci sequence. Ergod. Th. & Dynam. Sys. (2012) to appear.Google Scholar
Drmota, M. and Infusino, M.. On the discrepancy of some generalized Kakutani’s sequences of partitions. Unif. Distrib. Theory 7 (2012), 75–104.Google Scholar
Drmota, M. and Tichy, R. F.. Sequences, Discrepancies and Applications (Lecture Notes in Mathematics, 1651). Springer, Berlin, 1997.Google Scholar
Fraenkel, A. S.. Systems of numeration. Amer. Math. Monthly 92 (2) (1985), 105–114.Google Scholar
Frougny, C. and Solomyak, B.. Finite beta-expansions. Ergod. Th. & Dynam. Sys. 12 (1992), 713–723.Google Scholar
Grabner, P., Hellekalek, P. and Liardet, P.. The dynamical point of view of low-discrepancy sequences. Unif. Distrib. Theory 7 (1) (2012), 11–70.Google Scholar
Grabner, P., Liardet, P. and Tichy, R.. Odometers and systems of numeration. Acta Arith. 70 (1995), 103–123.CrossRefGoogle Scholar
Grabner, P. and Tichy, R.. Contributions to digit expansions with respect to linear recurring sequences. J. Number Theory 36 (1990), 160–169.CrossRefGoogle Scholar
Grabner, P. and Tichy, R.. $\alpha $-expansions, linear recurrences, and the sum-of-digits function. Manuscripta Math. 70 (1991), 311–324.Google Scholar
Halton, J. H.. On the efficiency of certain quasi-random sequences of points in evaluating multi-dimensional integrals. Numer. Math. 2 (1960), 84–90.Google Scholar
Hlawka, E.. Funktionen von beschränkter Variation in der Theorie der Gleichverteilung. Ann. Mat. Pura Appl. (54) (1961), 325–333.Google Scholar
Hollander, M.. Linear numeration systems, finite beta-expansions, and discrete spectrum of substitution dynamical systems. PhD Thesis, Washington University, 1996.Google Scholar
Kuipers, L. and Niederreiter, H.. Uniform Distribution of Sequences. Wiley-Interscience, New York, 1974.Google Scholar
Mori, M. and Mori, M.. Dynamical systems generated by algebraic method and low discrepancy sequences. Monte Carlo Methods Appl. 18 (2012), 327–351.Google Scholar
Ninomiya, S.. Constructing a new class of low-discrepancy sequences by using the $\beta $-adic transformation. Math. Comput. Simulation 47 (2) (1998), 403–418.Google Scholar
Ökten, G., Tuffin, B. and Burago, V.. A central limit theorem and improved error bounds for a hybrid-Monte Carlo sequence with applications in computational finance. J. Complexity 22 (4) (2006), 435–458.Google Scholar
Parry, W.. On the $\beta $-expansions of real numbers. Acta Math. Acad. Sci. Hungar. 11 (1960), 401–416.Google Scholar
Solomyak, B.. Substitutions, adic transformations and beta-expansions. Contemp. Math. 135 (1992), 361–372; (Proc. Conf. on Symbolic Dynamics, Yale, 1991).Google Scholar
Steiner, W.. Regularities of the distribution of $\beta $-adic van der Corput sequences. Monatsh. Math. 149 (1) (2006), 67–81.Google Scholar
Steiner, W.. Regularities of the distribution of abstract van der Corput sequences. Unif. Distrib. Theory 4 (2) (2009), 81–100.Google Scholar
Walters, P.. An Introduction to Ergodic Theory (Graduate Texts in Mathematics, 79). Springer, New York, 1982.Google Scholar
Weyl, H.. Über die Gleichverteilung von Zahlen mod. Eins. Math. Ann. 77 (1916), 313–352.Google Scholar