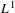 $L^{1}$
$L^{1}$Published online by Cambridge University Press: 18 August 2017
We show that  $\unicode[STIX]{x1D714}(n)$ and
$\unicode[STIX]{x1D714}(n)$ and 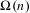 $\unicode[STIX]{x1D6FA}(n)$, the number of distinct prime factors of
$\unicode[STIX]{x1D6FA}(n)$, the number of distinct prime factors of  $n$ and the number of distinct prime factors of
$n$ and the number of distinct prime factors of  $n$ counted according to multiplicity, are good weighting functions for the pointwise ergodic theorem in
$n$ counted according to multiplicity, are good weighting functions for the pointwise ergodic theorem in 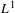 $L^{1}$. That is, if
$L^{1}$. That is, if  $g$ denotes one of these functions and
$g$ denotes one of these functions and 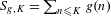 $S_{g,K}=\sum _{n\leq K}g(n)$, then for every ergodic dynamical system
$S_{g,K}=\sum _{n\leq K}g(n)$, then for every ergodic dynamical system 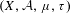 $(X,{\mathcal{A}},\unicode[STIX]{x1D707},\unicode[STIX]{x1D70F})$ and every
$(X,{\mathcal{A}},\unicode[STIX]{x1D707},\unicode[STIX]{x1D70F})$ and every 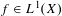 $f\in L^{1}(X)$,
$f\in L^{1}(X)$, 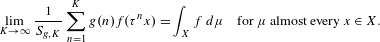 $$\begin{eqnarray}\lim _{K\rightarrow \infty }\frac{1}{S_{g,K}}\mathop{\sum }_{n=1}^{K}g(n)f(\unicode[STIX]{x1D70F}^{n}x)=\int _{X}f\,d\unicode[STIX]{x1D707}\quad \text{for }\unicode[STIX]{x1D707}\text{ almost every }x\in X.\end{eqnarray}$$
$$\begin{eqnarray}\lim _{K\rightarrow \infty }\frac{1}{S_{g,K}}\mathop{\sum }_{n=1}^{K}g(n)f(\unicode[STIX]{x1D70F}^{n}x)=\int _{X}f\,d\unicode[STIX]{x1D707}\quad \text{for }\unicode[STIX]{x1D707}\text{ almost every }x\in X.\end{eqnarray}$$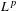 $L^{p}$,
$L^{p}$, 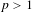 $p>1$.
$p>1$.