Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-28T09:52:33.272Z Has data issue: false hasContentIssue false
  • English
  • Français

Equilibrium measures for the Hénon map at the first bifurcation: uniqueness and geometric/statistical properties

Published online by Cambridge University Press:  02 October 2014

SAMUEL SENTI  and
HIROKI TAKAHASI
SAMUEL SENTI
Affiliation:
Instituto de Matematica, Universidade Federal do Rio de Janeiro, C.P. 68 530, CEP 21945-970, R.J., Brasil email [email protected]
HIROKI TAKAHASI
Affiliation:
Department of Mathematics, Keio University, Yokohama 223-8522, Japan email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

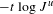For strongly dissipative Hénon maps at the first bifurcation parameter where the uniform hyperbolicity is destroyed by the formation of tangencies inside the limit set, we establish a thermodynamic formalism, i.e. we prove the existence and uniqueness of an invariant probability measure that minimizes the free energy associated with a non-continuous geometric potential $-t\log J^{u}$, where 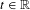$t\in \mathbb{R}$ is in a certain large interval and 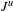$J^{u}$ denotes the Jacobian in the unstable direction. We obtain geometric and statistical properties of these measures.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 36 , Issue 1 , February 2016 , pp. 215 - 255
Copyright
© Cambridge University Press, 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bedford, E. and Smillie, J.. Real polynomial diffeomorphisms with maximal entropy: tangencies. Ann. Math. 160 (2004), 1–25.CrossRefGoogle Scholar
Bedford, E. and Smillie, J.. Real polynomial diffeomorphisms with maximal entropy: II. Small Jacobian. Ergod. Th. & Dynam. Sys. 26 (2006), 1259–1283.CrossRefGoogle Scholar
Benedicks, M. and Carleson, L.. The dynamics of the Hénon map. Ann. Math. 133 (1991), 73–169.CrossRefGoogle Scholar
Benedicks, M. and Viana, M.. Solution of the basin problem for Hénon-like attractors. Invent. Math. 143 (2001), 375–434.CrossRefGoogle Scholar
Benedicks, M. and Viana, M.. Random perturbations and statistical properties of Hénon-like maps. Ann. Inst. H. Poincaré Anal. Non Linéaire 23 (2006), 713–752.CrossRefGoogle Scholar
Benedicks, M. and Young, L.-S.. Sinai–Bowen–Ruelle measures for certain Hénon maps. Invent. Math. 112 (1993), 541–576.CrossRefGoogle Scholar
Benedicks, M. and Young, L.-S.. Markov extensions and decay of correlations for certain Hénon maps. Astérisque 261 (2000), 13–56.Google Scholar
Berger, P.. Abundance of one dimensional non uniformly hyperbolic attractors for surface endomorphisms. Preprint. http://arxiv.org/pdf/0903.1473.pdf.Google Scholar
Berger, P.. Properties of the maximal entropy measure and geometry of Hénon attractors. Preprint.http://arxiv.org/pdf/1202.2822.pdf.Google Scholar
Bowen, R.. Equilibrium States and the Ergodic Theory of Anosov Diffeomorphisms (Lecture Notes in Mathematics, 470). Springer, Berlin, 1975.CrossRefGoogle Scholar
Buzzi, J. and Sarig, S.. Uniqueness of equilibrium measures for countable Markov shifts and multidimensional piecewise expanding maps. Ergod. Th. & Dynam. Sys. 23 (2003), 1383–1400.CrossRefGoogle Scholar
Cao, Y., Luzzatto, S. and Rios, I.. The boundary of hyperbolicity for Hénon-like families. Ergod. Th. & Dynam. Sys. 28 (2008), 1049–1080.CrossRefGoogle Scholar
Devaney, R. and Nitecki, Z.. Shift automorphisms in the Hénon mapping. Commun. Math. Phys. 67 (1979), 137–146.CrossRefGoogle Scholar
Falconer, K.. Fractal Geometry. Mathematical Foundations and Applications. Wiley, Chichester, UK, 1990.Google Scholar
Hoensch, U. A.. Some hyperbolicity results for Hénon-like diffeomorphisms. Nonlinearity 21 (2008), 587–611.CrossRefGoogle Scholar
Jakobson, M.. Topological and metric properties of one-dimensional endomorphisms. Dokl. Akad. Nauk SSSR 243 (1978), 1452–1456.Google Scholar
Kac, M.. On the notion of recurrence in discrete stochastic processes. Bull. Amer. Math. Soc. 53 (1947), 1002–1010.CrossRefGoogle Scholar
Katok, A. and Hasselblatt, B.. Introduction to the Modern Theory of Dynamical Systems. Cambridge University Press, Cambridge, 1995.CrossRefGoogle Scholar
Ledrappier, F. and Young, L.-S.. The metric entropy of diffeomorphisms. Ann. Math. 122 (1985), 509–574.CrossRefGoogle Scholar
Leplaideur, R.. Thermodynamic formalism for a family of non-uniformly hyperbolic horseshoes and the unstable Jacobian. Ergod. Th. & Dynam. Sys. 31 (2011), 423–447.CrossRefGoogle Scholar
Leplaideur, R. and Rios, I.. Invariant manifolds and equilibrium states for non-uniformly hyperbolic horseshoes. Nonlinearity 18 (2005), 2847–2880.CrossRefGoogle Scholar
Leplaideur, R. and Rios, I.. On t-conformal measures and Hausdorff dimension for a family of non-uniformly hyperbolic horseshoes. Ergod. Th. & Dynam. Sys. 29 (2009), 1917–1950.CrossRefGoogle Scholar
Manning, A. and McCluskey, H.. Hausdorff-dimension for horseshoes. Ergod. Th. & Dynam. Sys. 3 (1983), 251–260.Google Scholar
Mauldin, R. D. and Urbański, M.. Gibbs states on the symbolic space over an infinite alphabet. Israel. J. Math. 125 (2001), 93–130.CrossRefGoogle Scholar
Mora, L. and Viana, M.. Abundance of strange attractors. Acta Math. 171 (1993), 1–71.CrossRefGoogle Scholar
Palis, J. and Takens, S.. Hyperbolicity & Sensitive Chaotic Dynamics at Homoclinic Bifurcations (Cambridge Studies in Advanced Mathematics, 35). Cambridge University Press, Cambridge, 1993.Google Scholar
Pesin, Ya.. Families of invariant manifolds which correspond to non-vanishing Lyapunov exponents. Math. USSR-Izv. 10 (1976), 1261–1305.CrossRefGoogle Scholar
Pesin, Ya. and Senti, S.. Equilibrium measures for maps with inducing schemes. J. Mod. Dyn. 2 (2008), 1–31.Google Scholar
Pesin, Ya., Senti, S. and Zhang, K.. Thermodynamics of towers of hyperbolic type. Preprint. http://arxiv.org/pdf/1403.2989.pdf.Google Scholar
Rios, I.. Unfolding of homoclinic tangencies inside horseshoes: hyperbolicity, fractal dimensions and persistent tangencies. Nonlinearity 14 (2001), 431–462.CrossRefGoogle Scholar
Rokhlin, V. A.. Lectures on the theory of entropy of transformation with invariant measure. Uspekhi Mat. Nauk. 22 (1967), 3–56; Engl. transl: Russian Math. Surveys 22 (1967) 1–52.Google Scholar
Ruelle, D.. An inequality for the entropy of differentiable maps. Bol. Soc. Brasil. Math. 9 (1978), 83–87.CrossRefGoogle Scholar
Ruelle, D.. Thermodynamic Formalism. The Mathematical Structures of Classical Equilibrium Statistical Mechanics (Encyclopedia of Mathematics and its Applications, 5). Addison-Wesley, Reading, MA.Google Scholar
Ruelle, D.. Ergodic theory of differentiable dynamical systems. Publ. Math. I.H.E.S. 50 (1979), 27–58.CrossRefGoogle Scholar
Sarig, O.. Thermodynamic formalism for countable Markov shifts. Ergod. Th. & Dynam. Sys. 19 (1999), 1565–1593.CrossRefGoogle Scholar
Sarig, O.. Existence of Gibbs measures or countable Markov shifts. Proc. Amer. Math. Soc. 131(6) (2003), 1751–1758.CrossRefGoogle Scholar
Senti, S. and Takahasi, H.. Equilibrium measures for the Hénon map at the first bifurcation. Nonlinearity 26 (2013), 1719–1741.CrossRefGoogle Scholar
Sinai, Y.. Gibbs measures in ergodic theory. Uspekhi Mat. Nauk. 27 (1972), 21–64.Google Scholar
Takahasi, H.. Abundance of non-uniform hyperbolicity in bifurcations of surface endomorphisms. Tokyo J. Math. 34 (2011), 53–113.CrossRefGoogle Scholar
Takahasi, H.. Prevalent dynamics at the first bifurcation of Hénon-like families. Commun. Math. Phys. 312 (2012), 37–85.CrossRefGoogle Scholar
Urbański, M. and Wolf, C.. Ergodic theory of parabolic horseshoes. Commun. Math. Phys. 281 (2008), 711–751.CrossRefGoogle Scholar
Wang, Q. D. and Young, L.-S.. Strange attractors with one direction of instability. Commun. Math. Phys. 218 (2001), 1–97.CrossRefGoogle Scholar
William, F.. An Introduction to Probability Theory and its Applications, 3rd edn. Vol. 1. Wiley, New York, 1968.Google Scholar
Young, L.-S.. Statistical properties of dynamical systems with some hyperbolicity. Ann. Math. 147 (1998), 585–650.CrossRefGoogle Scholar
Zweimüller, R.. Invariant measures for general(ized) induced transformations. Proc. Amer. Math. Soc. 133 (2005), 2283–2295.CrossRefGoogle Scholar