No CrossRef data available.
Published online by Cambridge University Press: 04 January 2013
Using the works of Mañé [On the topological entropy of the geodesic flows. J. Differential Geom.45 (1989), 74–93] and Paternain [Topological pressure for geodesic flows. Ann. Sci. Éc. Norm. Supér. (4) 33 (2000), 121–138] we study the distribution of geodesic arcs with respect to equilibrium states of the geodesic flow on a closed manifold, equipped with a 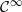 $\mathcal {C}^{\infty }$Riemannian metric. We prove large-deviation lower and upper bounds and a contraction principle for the geodesic flow in the space of probability measures of the unit tangent bundle. We deduce a way of approximating equilibrium states for continuous potentials.
$\mathcal {C}^{\infty }$Riemannian metric. We prove large-deviation lower and upper bounds and a contraction principle for the geodesic flow in the space of probability measures of the unit tangent bundle. We deduce a way of approximating equilibrium states for continuous potentials.