Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-16T17:02:32.823Z Has data issue: false hasContentIssue false
  • English
  • Français

Enveloping semigroups and quasi-discrete spectrum

Published online by Cambridge University Press:  15 June 2015

JUHO RAUTIO
JUHO RAUTIO*
Affiliation:
University of Oulu, Department of Mathematical Sciences, PL 8000, FI-90014 Oulun yliopisto, Finland email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The structures of the enveloping semigroups of certain elementary finite- and infinite-dimensional distal dynamical systems are given, answering open problems posed in 1982 by Namioka [Ellis groups and compact right topological groups. Conference in Modern Analysis and Probability (New Haven, CT, 1982) (Contemporary Mathematics, 26). American Mathematical Society, Providence, RI, 1984, 295–300]. The universal minimal system with (topological) quasi-discrete spectrum is obtained from the infinite-dimensional case. It is proved that, on the one hand, a minimal system is a factor of this universal system if and only if its enveloping semigroup has quasi-discrete spectrum and that, on the other hand, such a factor need not have quasi-discrete spectrum in itself. This leads to a natural generalization of the property of having quasi-discrete spectrum, which is named the 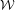${\mathcal{W}}$ -property.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 36 , Issue 8 , December 2016 , pp. 2627 - 2660
Copyright
© Cambridge University Press, 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abramov, L. M.. Metric automorphisms with quasi-discrete spectrum. Izv. Akad. Nauk SSSR Ser. Mat. 26 (1962), 513–530.Google Scholar
Auslander, J.. Minimal Flows and Their Extensions. North-Holland, Amsterdam, 1988.Google Scholar
Berglund, J. F., Junghenn, H.D. and Milnes, P.. Analysis on Semigroups. John Wiley & Sons, New York, 1989.Google Scholar
Brown, J. R.. A universal model for dynamical systems with quasi-discrete spectrum. Bull. Amer. Math. Soc. 75 (1969), 1028–1030.Google Scholar
Donoso, S.. Enveloping semigroups of systems of order d . Discrete Contin. Dyn. Syst. 34 (2014), 2729–2740.Google Scholar
Furstenberg, H.. Strict ergodicity and transformation of the torus. Amer. J. Math. 83 (1961), 573–601.Google Scholar
Furstenberg, H.. The structure of distal flows. Amer. J. Math. 85 (1963), 477–515.CrossRefGoogle Scholar
Glasner, E.. Minimal nil-transformations of class two. Israel J. Math. 81 (1993), 31–51.Google Scholar
Glasner, E.. Enveloping semigroups in topological dynamics. Topology Appl. 154 (2007), 2344–2363.Google Scholar
Hahn, F.. Skew product transformations and the algebras generated by exp(p (n)). Illionois J. Math. 9 (1965), 178–190.Google Scholar
Hahn, F. and Parry, W.. Minimal dynamical systems with quasi-discrete spectrum. J. Lond. Math. Soc. 40 (1965), 309–323.Google Scholar
Hahn, F. and Parry, W.. Some characteristic properties of dynamical systems with quasi-discrete spectra. Math. Systems Theory 2 (1968), 179–190.CrossRefGoogle Scholar
Hewitt, E. and Ross, K. A.. Abstract Harmonic Analysis, Vol. I (Grundlehren der Mathematischen Wissenschaften, 115) . Springer, Berlin, 1963.Google Scholar
Host, B., Kra, B. and Maass, A.. Nilsequences and a structure theorem for topological dynamical systems. Adv. Math. 224 (2010), 103–129.CrossRefGoogle Scholar
Jabbari, A. and Namioka, I.. Ellis group and the topological center of the flow generated by the map n↦𝜆 n k . Milan J. Math. 78 (2010), 503–522.CrossRefGoogle Scholar
Kuipers, L. and Niederreiter, H.. Uniform Distribution of Sequences. Wiley-Interscience, New York, 1974.Google Scholar
Lawton, B.. A note on well distributed sequences. Proc. Amer. Math. Soc. 10 (1959), 891–893.CrossRefGoogle Scholar
Milnes, P.. Ellis groups and group extensions. Houston J. Math. 12 (1986), 87–108.Google Scholar
Namioka, I.. Ellis groups and compact right topological groups. Conference in Modern Analysis and Probability (New Haven, CT, 1982) (Contemporary Mathematics, 26) . American Mathematical Society, Providence, RI, 1984, pp. 295–300.Google Scholar
Parry, W.. Compact abelian group extensions of discrete dynamical systems. Z. Wahrscheinlichkeitstheorie Verw. Gebiete 13 (1969), 95–113.CrossRefGoogle Scholar
Pikuła, R.. Enveloping semigroups of unipotent affine transformations of the torus. Ergod. Th. & Dynam. Sys. 30 (2010), 1543–1559.Google Scholar
Robertson, J. B.. Ergodic measure preserving transformations with quasi-discrete spectrum. Trans. Amer. Math. Soc. 190 (1974), 301–311.CrossRefGoogle Scholar
Salehi, E.. Distal functions and unique ergodicity. Trans. Amer. Math. Soc. 323 (1991), 703–713.Google Scholar
de Vries, J.. Elements of Topological Dynamics. Kluwer Academic, Dordrecht, 1993.CrossRefGoogle Scholar