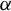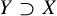1 Introduction
The entropy of a subshift X is the limit of
![]() $({\log |\mathcal {L}_n(X)|})/{n}$
where
$({\log |\mathcal {L}_n(X)|})/{n}$
where
![]() $\mathcal {L}_n(X)$
is the set of words in X of length n, as
$\mathcal {L}_n(X)$
is the set of words in X of length n, as
![]() $n \rightarrow \infty $
. It measures the amount of information in orbits of this dynamical system. There are several ways to quantify how this information is produced. One is the entropy pairs relation, due to Blanchard [Reference Blanchard and Walters3, Reference Blanchard4], which intuitively measures the amount of information in orbits when we obtain information only when the point is very close to one of two points (the elements of the entropy pair).
$n \rightarrow \infty $
. It measures the amount of information in orbits of this dynamical system. There are several ways to quantify how this information is produced. One is the entropy pairs relation, due to Blanchard [Reference Blanchard and Walters3, Reference Blanchard4], which intuitively measures the amount of information in orbits when we obtain information only when the point is very close to one of two points (the elements of the entropy pair).
The entropy pairs relation (plus the diagonal) is symmetric, reflexive, and topologically closed but not necessarily transitive, and a subshift turns out to have only positive entropy (non-trivial) factors if and only if the smallest closed equivalence relation containing the entropy pairs relation is the full relation [Reference Blanchard4]. The hierarchy generated by alternately closing the relation topologically and transitively is studied in [Reference Barbieri and García-Ramos2], and it is shown that the full relation can arise at any countable ordinal. We refer to [Reference Barbieri and García-Ramos2] for the state-of-the-art and further context.
Our main contribution is that such examples can be made expansive. We prove this using relatively general subshift constructions, in particular, Lemma 5 and Proposition 6 construct a large class of relations as entropy pair relations, which may be of independent interest.
By alternating topological and transitive closure on a symmetric reflexive relation E, one obtains an ordinal-indexed tower of equivalence relations. The union of these equivalence relations is, of course, just the smallest closed equivalence relation containing E.
Definition 1. Let X be a topological space and
![]() $E \subset X^2$
a symmetric reflexive relation. If E is closed, let
$E \subset X^2$
a symmetric reflexive relation. If E is closed, let
![]() $\zeta = 1$
, otherwise
$\zeta = 1$
, otherwise
![]() $\zeta = 0$
. Define
$\zeta = 0$
. Define
![]() $E^{(\zeta )} = E$
and write any ordinal greater than
$E^{(\zeta )} = E$
and write any ordinal greater than
![]() $\zeta $
in the unique way as
$\zeta $
in the unique way as
![]() $\lambda + 2n + b$
,
$\lambda + 2n + b$
,
![]() $\lambda $
a limit ordinal (including
$\lambda $
a limit ordinal (including
![]() $0$
),
$0$
),
![]() $n \in \mathbb {N}, b \in \{0,1\}$
, and define
$n \in \mathbb {N}, b \in \{0,1\}$
, and define
 $$ \begin{align*} E^{(\lambda + 2n + 1)} &= \overline{E^{(\lambda + 2n)}}\qquad\quad {\mbox{(topological closure)}}, \\[6pt]E^{(\lambda + 2(n + 1))} &= (E^{(\lambda + 2n + 1)})^* \quad \text{(transitive closure)}, \\[6pt]E^{(\lim_i \lambda_i)} &= \bigcup_{i} E^{(\lambda_i)}. \end{align*} $$
$$ \begin{align*} E^{(\lambda + 2n + 1)} &= \overline{E^{(\lambda + 2n)}}\qquad\quad {\mbox{(topological closure)}}, \\[6pt]E^{(\lambda + 2(n + 1))} &= (E^{(\lambda + 2n + 1)})^* \quad \text{(transitive closure)}, \\[6pt]E^{(\lim_i \lambda_i)} &= \bigcup_{i} E^{(\lambda_i)}. \end{align*} $$
We say the close-up rank of E is the least
![]() $\lambda $
such that
$\lambda $
such that
![]() $E^{(\lambda )} = E^{(\lambda +1)}$
. We say E is equalizing if
$E^{(\lambda )} = E^{(\lambda +1)}$
. We say E is equalizing if
![]() $E^{(\lambda )} = X^2$
for some
$E^{(\lambda )} = X^2$
for some
![]() $\lambda $
.
$\lambda $
.
Ordinals
![]() $\lambda + 2n + b$
where
$\lambda + 2n + b$
where
![]() $b = 0$
are called even, and others odd.
$b = 0$
are called even, and others odd.
The check for topological closedness is made in the beginning so that
![]() $E^{(\lambda )}$
is always topologically closed at odd ordinals.
$E^{(\lambda )}$
is always topologically closed at odd ordinals.
Lemma 2. Let
![]() $\lambda \geq 1$
be a countable ordinal. Then there exists a closed countable set
$\lambda \geq 1$
be a countable ordinal. Then there exists a closed countable set
![]() $X \subset [0,1]$
and an equalizing closed symmetric reflexive relation
$X \subset [0,1]$
and an equalizing closed symmetric reflexive relation
![]() $E \subset X^2$
with rank
$E \subset X^2$
with rank
![]() $\lambda $
.
$\lambda $
.
For this, we arrange an ordinal of the form
![]() $\omega ^{\alpha }$
or
$\omega ^{\alpha }$
or
![]() $\omega ^{\alpha } + 1$
on the circle and join each point with its successor. The calculation of the close-up rank roughly then corresponds to the computation of the Hausdorff or Cantor–Bendixson rank of the ordinal.
$\omega ^{\alpha } + 1$
on the circle and join each point with its successor. The calculation of the close-up rank roughly then corresponds to the computation of the Hausdorff or Cantor–Bendixson rank of the ordinal.
In [Reference Barbieri and García-Ramos2], Barbieri and García-Ramos study the close-up process for the closed equivalence relation
![]() $\mathrm {EP}(X) = E \cup \Delta $
where
$\mathrm {EP}(X) = E \cup \Delta $
where
![]() $\Delta $
is the diagonal and E is the family of entropy pairs of the compact topological dynamical system
$\Delta $
is the diagonal and E is the family of entropy pairs of the compact topological dynamical system
![]() $(G, X)$
(G an amenable discrete group acting on X), and where
$(G, X)$
(G an amenable discrete group acting on X), and where
![]() $(x, y)$
is an entropy pair if the open cover
$(x, y)$
is an entropy pair if the open cover
![]() $(U^c, V^c)$
has positive entropy [Reference Denker, Grillenberger and Sigmund5, Definition 14.5] for all disjoint closed neighborhoods
$(U^c, V^c)$
has positive entropy [Reference Denker, Grillenberger and Sigmund5, Definition 14.5] for all disjoint closed neighborhoods
![]() $U \ni x, V \ni y$
.
$U \ni x, V \ni y$
.
In [Reference Barbieri and García-Ramos2], a dynamical system is defined to be of complete positive entropy (CPE) class
![]() $\alpha $
if the equivalence relation
$\alpha $
if the equivalence relation
![]() $E \cup \Delta $
is equalizing with rank
$E \cup \Delta $
is equalizing with rank
![]() $\alpha $
. One of the results of [Reference Barbieri and García-Ramos2] is that among abstract dynamical systems, the CPE class
$\alpha $
. One of the results of [Reference Barbieri and García-Ramos2] is that among abstract dynamical systems, the CPE class
![]() $\alpha $
is non-empty for every countable amenable group G.
$\alpha $
is non-empty for every countable amenable group G.
Nishant Chandgotia asked in personal communication if there is a subshift realization of their process, that is, whether there is a subshift in the CPE class
![]() $\alpha $
. We prove a positive answer for
$\alpha $
. We prove a positive answer for
![]() $G = \mathbb {Z}$
.
$G = \mathbb {Z}$
.
Theorem 3. Let
![]() $\alpha \geq 1$
be a countable ordinal. Then there exists a subshift
$\alpha \geq 1$
be a countable ordinal. Then there exists a subshift
![]() $X \subset A^{\mathbb {Z}}$
in CPE class
$X \subset A^{\mathbb {Z}}$
in CPE class
![]() $\alpha $
.
$\alpha $
.
We prove this by first implementing closed relations on topological spaces as shift-invariant relations on subshifts, and then implementing such relations as CPE pairs.
A point
![]() $x \in A^{\mathbb {Z}}$
is Toeplitz if
$x \in A^{\mathbb {Z}}$
is Toeplitz if
![]() $\text { for all } i \in \mathbb {Z}: \text {there exists } n> 0: \text {for all } m \in \mathbb {Z}: x_{i+mn}$
$\text { for all } i \in \mathbb {Z}: \text {there exists } n> 0: \text {for all } m \in \mathbb {Z}: x_{i+mn}$
![]() $= x_i$
. (Often one excludes the periodic points; indeed in our application, the points are never periodic, but we omit this requirement so we need not address it explicitly.) A Toeplitz subshift is a subshift generated by a Toeplitz point. A pointwise zero-entropy Toeplitz subshift is one where every point generates a Toeplitz subshift with zero entropy. By the variational principle, a pointwise zero-entropy Toeplitz subshift has zero-entropy, since any generic point for an ergodic measure of positive entropy would generate a Toeplitz subshift with positive entropy (see e.g. §18 and equation (13.3) in [Reference Denker, Grillenberger and Sigmund5]).
$= x_i$
. (Often one excludes the periodic points; indeed in our application, the points are never periodic, but we omit this requirement so we need not address it explicitly.) A Toeplitz subshift is a subshift generated by a Toeplitz point. A pointwise zero-entropy Toeplitz subshift is one where every point generates a Toeplitz subshift with zero entropy. By the variational principle, a pointwise zero-entropy Toeplitz subshift has zero-entropy, since any generic point for an ergodic measure of positive entropy would generate a Toeplitz subshift with positive entropy (see e.g. §18 and equation (13.3) in [Reference Denker, Grillenberger and Sigmund5]).
If X is a topological space, the hit-or-miss topology on its closed subsets has subbasis
where U ranges over open sets of X and K over compact sets of X. For the space of closed subsets of a subshift, this is equal to the topology given by Hausdorff distance [Reference Kuratowski11], and compares the set of words up to length n. This is the topology we use for the space of subshifts of a subshift X. The minimal subshifts form a subspace, and we give it the induced topology. (This subspace need not be closed, consider for example the space of minimal subshifts of the Grand Sturmian subshift [Reference Kůrka12], where obviously no sequence of Sturmian subshifts with density of
![]() $1$
s properly decreasing to zero has a converging subsequence.)
$1$
s properly decreasing to zero has a converging subsequence.)
Lemma 4. For any compact metrizable zero-dimensional space Z, there exists a pointwise zero-entropy Toeplitz subshift X and an open quotient map
![]() $\phi : X \to Z$
such that
$\phi : X \to Z$
such that
![]() $\phi ^{-1}(z)$
is a minimal subshift for every
$\phi ^{-1}(z)$
is a minimal subshift for every
![]() $z \in Z$
, and
$z \in Z$
, and
![]() $\phi $
induces a homeomorphism between Z and the space of minimal subshifts of X.
$\phi $
induces a homeomorphism between Z and the space of minimal subshifts of X.
The construction is not new (see e.g. [Reference Ballier1] for a more general construction in the recursive category), although we do not know a reference that checks the stated topological dynamical properties. The important word in the above statement is ‘open’—intuitively, because taking preimages of relations in an open quotient map induces a ‘close-up process homomorphism’, in particular, the close-up rank is preserved.
We show that any close-up process on a subshift, satisfying some strong technical assumptions, can be realized as the entropy pairs process. We say a relation
![]() $E \subset X^2$
is doubly shift-invariant if it is invariant under the action of
$E \subset X^2$
is doubly shift-invariant if it is invariant under the action of
![]() $\mathbb {Z}^2$
that shifts the two components separately. If
$\mathbb {Z}^2$
that shifts the two components separately. If
![]() $\lambda $
is a successor ordinal, write
$\lambda $
is a successor ordinal, write
![]() $\lambda -1$
for its predecessor.
$\lambda -1$
for its predecessor.
If
![]() $E \subset X^2$
is a relation, write
$E \subset X^2$
is a relation, write
![]() $E^{[k]} = \{(x_1,x_2,\ldots ,x_k) \;|\; \text { for all } i,j: (x_i,x_j) \in E\}$
(so
$E^{[k]} = \{(x_1,x_2,\ldots ,x_k) \;|\; \text { for all } i,j: (x_i,x_j) \in E\}$
(so
![]() $E = E^{[2]}$
if and only if E is symmetric).
$E = E^{[2]}$
if and only if E is symmetric).
Lemma 5. Let
![]() $X \subset A^{\mathbb {Z}}$
be a subshift with zero entropy and let
$X \subset A^{\mathbb {Z}}$
be a subshift with zero entropy and let
![]() $E \subset X^2$
be a closed doubly shift-invariant symmetric reflexive relation. Then there exists a subshift Y with
$E \subset X^2$
be a closed doubly shift-invariant symmetric reflexive relation. Then there exists a subshift Y with
![]() ${X \subset Y \subset \hat A^{\mathbb {Z}}}$
(over a possibly larger alphabet
${X \subset Y \subset \hat A^{\mathbb {Z}}}$
(over a possibly larger alphabet
![]() $\hat A \supset A$
) such that
$\hat A \supset A$
) such that
![]() ${\mathrm {EP}(Y)^{(\lambda )} \cap X^2 = E^{(\lambda )}}$
for all
${\mathrm {EP}(Y)^{(\lambda )} \cap X^2 = E^{(\lambda )}}$
for all
![]() $\lambda $
. Furthermore, if
$\lambda $
. Furthermore, if
![]() $E^{(\lambda )} \cap X^2 = X^2$
, then
$E^{(\lambda )} \cap X^2 = X^2$
, then
![]() $\mathrm {EP}(Y)^{(\lambda +1)} = Y^2$
, and we have
$\mathrm {EP}(Y)^{(\lambda +1)} = Y^2$
, and we have
![]() ${\mathrm {EP}(Y)^{(\lambda )} = Y^2}$
if:
${\mathrm {EP}(Y)^{(\lambda )} = Y^2}$
if:
-
•
 $\lambda $
is even; or
$\lambda $
is even; or -
•
 $\lambda $
is odd and
$\lambda $
is odd and
 $(E^{[k]})^2 \subset \overline {(E^{(\lambda -1)})^{[2k]} \cap (E^{[k]})^2}$
.
$(E^{[k]})^2 \subset \overline {(E^{(\lambda -1)})^{[2k]} \cap (E^{[k]})^2}$
.
The intuitive description is that we add an entropy-generating supersystem on top of X, by allowing alternation between words from the two points from X (separated by a special symbol) if and only if they are in the relation E. We want that X originally has no entropy pairs, so we require it has zero entropy.
For
![]() $A \in X^k$
and
$A \in X^k$
and
![]() $B \in X^k$
, we can think of the pair
$B \in X^k$
, we can think of the pair
![]() $(A, B)$
as an element
$(A, B)$
as an element
![]() $(A, B) \in X^{2k}$
in a natural way. For some intuition behind the odd condition in Lemma 5 for odd
$(A, B) \in X^{2k}$
in a natural way. For some intuition behind the odd condition in Lemma 5 for odd
![]() $\lambda> 2$
, first note that
$\lambda> 2$
, first note that
![]() $(E^{[k]})^2 \subset \overline {(E^{(\lambda -1)})^{[2k]} \cap (E^{[k]})^2}$
means precisely that if
$(E^{[k]})^2 \subset \overline {(E^{(\lambda -1)})^{[2k]} \cap (E^{[k]})^2}$
means precisely that if
![]() $A, B \in E^{[k]}$
, then either
$A, B \in E^{[k]}$
, then either
![]() $(a,b) \in E^{(\lambda -1)}$
for some
$(a,b) \in E^{(\lambda -1)}$
for some
![]() $a \in A$
and
$a \in A$
and
![]() $b \in B$
(equivalently
$b \in B$
(equivalently
![]() $(A, B) \in (E^{(\lambda -1)})^{[2k]}$
by the transitivity of
$(A, B) \in (E^{(\lambda -1)})^{[2k]}$
by the transitivity of
![]() $E^{(\lambda -1)}$
), or we can find
$E^{(\lambda -1)}$
), or we can find
![]() $A_i, B_i \in E^{[k]}$
such that
$A_i, B_i \in E^{[k]}$
such that
![]() $(A_i, B_i) \in (E^{(\lambda -1)})^{[2k]}$
and
$(A_i, B_i) \in (E^{(\lambda -1)})^{[2k]}$
and
![]() $(A_i, B_i) \rightarrow (A, B)$
.
$(A_i, B_i) \rightarrow (A, B)$
.
This condition arises from the construction method: In the subshift Y, points encode finite tuples of points from X, any pair of which is in the relation. Elements of Y thus roughly correspond to elements of
![]() $E^{[k]}$
, and we want that at the final limit step, any pair of points in Y (roughly corresponding to an element of
$E^{[k]}$
, and we want that at the final limit step, any pair of points in Y (roughly corresponding to an element of
![]() $(E^{[k]})^2$
) can be approximated by a pair of points from Y which are in the relation at the previous step, which in terms of the close-up process of E translates to being in
$(E^{[k]})^2$
) can be approximated by a pair of points from Y which are in the relation at the previous step, which in terms of the close-up process of E translates to being in
![]() $(E^{(\lambda -1)})^{[2k]}$
. Not every relation satisfies the odd condition, see Example 1.
$(E^{(\lambda -1)})^{[2k]}$
. Not every relation satisfies the odd condition, see Example 1.
This odd condition holds in the construction proving Lemma 2 (see Lemma 7 for the precise statement), and is preserved under open quotients, so it passes to the subshift implementations of abstract processes given by Lemma 4.
We do not know to what extent double shift-invariance, the zero-entropy assumption, and the odd condition can be weakened in the previous lemma. Out of general interest, for implementing any relation as entropy pairs of a supersystem (without precise control on the entropy pairs involving the new points), we provide a simpler construction.
Proposition 6. Suppose X has zero entropy and
![]() $E \subset X^2$
is a closed symmetric reflexive shift-invariant relation. Then there exists a subshift Y with
$E \subset X^2$
is a closed symmetric reflexive shift-invariant relation. Then there exists a subshift Y with
![]() $X \subset Y \subset \hat A^{\mathbb {Z}}$
(over a possibly larger alphabet
$X \subset Y \subset \hat A^{\mathbb {Z}}$
(over a possibly larger alphabet
![]() $\hat A \supset A$
) such that
$\hat A \supset A$
) such that
![]() $\mathrm {EP}(Y) \cap X^2 = E$
.
$\mathrm {EP}(Y) \cap X^2 = E$
.
This is optimal in the sense that for positive entropy X, it fails for E the diagonal relation [Reference Barbieri and García-Ramos2, Reference Blanchard4, Reference Kerr and Li10], and for X zero-entropy and for any
![]() $Y \supset X$
,
$Y \supset X$
,
![]() $\mathrm {EP}(Y) \cap X^2$
is closed symmetric reflexive shift-invariant. One could, however, ask for the aesthetically more pleasing
$\mathrm {EP}(Y) \cap X^2$
is closed symmetric reflexive shift-invariant. One could, however, ask for the aesthetically more pleasing
![]() $\mathrm {EP}(Y) = E \cup \Delta _Y$
instead of just
$\mathrm {EP}(Y) = E \cup \Delta _Y$
instead of just
![]() $\mathrm {EP}(Y) \cap X^2 = E$
, and we conjecture that this can be done. Even further, one could consider X with positive entropy, and restrict to relations containing
$\mathrm {EP}(Y) \cap X^2 = E$
, and we conjecture that this can be done. Even further, one could consider X with positive entropy, and restrict to relations containing
![]() $\mathrm {EP}(X)$
.
$\mathrm {EP}(X)$
.
The constructions are made for
![]() $\mathbb {Z}$
, and of course one can ask whether they can be generalized to general amenable groups. We conjecture that all CPE classes are inhabited by subshifts on all countable amenable groups.
$\mathbb {Z}$
, and of course one can ask whether they can be generalized to general amenable groups. We conjecture that all CPE classes are inhabited by subshifts on all countable amenable groups.
Particularly in the case of
![]() $\mathbb {Z}^d$
, one can also ask if this can be done by subshifts of finite type (SFTs). We conjecture that
$\mathbb {Z}^d$
, one can also ask if this can be done by subshifts of finite type (SFTs). We conjecture that
![]() $\mathbb {Z}^2$
-SFTs inhabit exactly the CPE classes
$\mathbb {Z}^2$
-SFTs inhabit exactly the CPE classes
![]() $\alpha $
where
$\alpha $
where
![]() $\alpha $
is recursive. (This has been proved by Westrick [Reference Westrick14] (independently of our conjecture).)
$\alpha $
is recursive. (This has been proved by Westrick [Reference Westrick14] (independently of our conjecture).)
2 Definitions and conventions
A topological dynamical system is
![]() $(X,f)$
where X is a compact metrizable space and
$(X,f)$
where X is a compact metrizable space and
![]() $f : X \to X$
a homeomorphism. The full shift is the dynamical system
$f : X \to X$
a homeomorphism. The full shift is the dynamical system
![]() $(A^{\mathbb {Z}}, \sigma )$
, where A is a finite set and
$(A^{\mathbb {Z}}, \sigma )$
, where A is a finite set and
![]() $A^{\mathbb {Z}}$
has the (Cantor) product topology, and
$A^{\mathbb {Z}}$
has the (Cantor) product topology, and
![]() $\sigma (x)_i = x_{i+1}$
is the left shift. A subshift is a closed
$\sigma (x)_i = x_{i+1}$
is the left shift. A subshift is a closed
![]() $\sigma $
-invariant subsystem of the full shift. A subshift is minimal if it does not contain non-empty proper subshifts. Topological dynamical systems form a category with morphisms the dynamics-commuting continuous maps. A cover of a dynamical system Y refers to a surjective morphism
$\sigma $
-invariant subsystem of the full shift. A subshift is minimal if it does not contain non-empty proper subshifts. Topological dynamical systems form a category with morphisms the dynamics-commuting continuous maps. A cover of a dynamical system Y refers to a surjective morphism
![]() $g : X \to Y$
, or its domain X. A cover is almost one-to-one if the set of points with a unique preimage is dense. See any standard reference for the basic theory and definitions related to topological entropy [Reference Denker, Grillenberger and Sigmund5].
$g : X \to Y$
, or its domain X. A cover is almost one-to-one if the set of points with a unique preimage is dense. See any standard reference for the basic theory and definitions related to topological entropy [Reference Denker, Grillenberger and Sigmund5].
We denote the real interval as
![]() $[0,1]$
, but other than this, our intervals
$[0,1]$
, but other than this, our intervals
![]() $[a, b]$
are usually interpreted as discrete, which should not cause confusion. Words—finite or infinite—are functions from contiguous subsets of
$[a, b]$
are usually interpreted as discrete, which should not cause confusion. Words—finite or infinite—are functions from contiguous subsets of
![]() $\mathbb {Z}$
to a (by default finite) alphabet. We typically call infinite words points, as we think of them as points of the full shift dynamical system (or another subshift). Positioning conventions (precise domains of words) should always be clear from context, or are explained when used. By default, we identify words whose domains are translates of each other and the letters are correspondingly translated, so finite words can be seen as functions
$\mathbb {Z}$
to a (by default finite) alphabet. We typically call infinite words points, as we think of them as points of the full shift dynamical system (or another subshift). Positioning conventions (precise domains of words) should always be clear from context, or are explained when used. By default, we identify words whose domains are translates of each other and the letters are correspondingly translated, so finite words can be seen as functions
![]() $w : [0,n-1] \to A$
. Concatenation of words is presented by
$w : [0,n-1] \to A$
. Concatenation of words is presented by
![]() $u\cdot v$
or
$u\cdot v$
or
![]() $uv$
. A point
$uv$
. A point
![]() $x \in A^{\mathbb {N}}$
is eventually constant if
$x \in A^{\mathbb {N}}$
is eventually constant if
![]() $\text { there exists } n: \text { for all } i \geq n: x_i$
$\text { there exists } n: \text { for all } i \geq n: x_i$
![]() $ = x_{i+1}$
.
$ = x_{i+1}$
.
A (deterministic) substitution is a map
![]() $\tau : A \to B^*$
where
$\tau : A \to B^*$
where
![]() $A,B$
are (possibly infinite) alphabets, and
$A,B$
are (possibly infinite) alphabets, and
![]() $B^*$
denotes the set of finite words over B, including the empty word. We can apply a substitution to a word or a point by replacing the individual symbols
$B^*$
denotes the set of finite words over B, including the empty word. We can apply a substitution to a word or a point by replacing the individual symbols
![]() $a \in A$
by words
$a \in A$
by words
![]() $\tau (a)$
. A non-deterministic substitution is a function
$\tau (a)$
. A non-deterministic substitution is a function
![]() $\tau : A \to \mathcal {P}(B^*)$
where
$\tau : A \to \mathcal {P}(B^*)$
where
![]() $\mathcal {P}$
denotes the power set. Applying a non-deterministic substitution to a word or point (or a set of words or points) results in the set of all words or points obtainable by replacing each symbol
$\mathcal {P}$
denotes the power set. Applying a non-deterministic substitution to a word or point (or a set of words or points) results in the set of all words or points obtainable by replacing each symbol
![]() $a \in A$
by one of its images
$a \in A$
by one of its images
![]() $w \in \tau (a)$
(independently for each occurrence of the symbol).
$w \in \tau (a)$
(independently for each occurrence of the symbol).
3 The proofs
3.1 Close-up processes of arbitrary length
See any standard reference for definitions and basic properties of ordinal arithmetic (e.g. [Reference Hrbacek and Jech9]). The following lemma is roughly just the computation of the Hausdorff rank of a (cyclic) order corresponding to an ordinal. Since the definition of the close-up process involves parity and the restriction to compact spaces leads to a small issue with non-compact ordinals, it seems easier to give a direct proof than to find a reference.
Lemma 7. Let
![]() $\lambda \geq 1$
be a countable ordinal. Then there exists a closed countable set
$\lambda \geq 1$
be a countable ordinal. Then there exists a closed countable set
![]() $X \subset [0,1]$
and an equalizing closed symmetric reflexive relation
$X \subset [0,1]$
and an equalizing closed symmetric reflexive relation
![]() $E \subset X^2$
with rank
$E \subset X^2$
with rank
![]() $\lambda $
. Furthermore, if
$\lambda $
. Furthermore, if
![]() $\lambda> 2$
is an odd ordinal, then
$\lambda> 2$
is an odd ordinal, then
![]() $(E^{[k]})^2 \subset \overline {(E^{(\lambda -1)})^{[2k]} \cap (E^{[k]})^2}$
.
$(E^{[k]})^2 \subset \overline {(E^{(\lambda -1)})^{[2k]} \cap (E^{[k]})^2}$
.
Proof. To each
![]() $\alpha = \omega ^{\zeta }$
or
$\alpha = \omega ^{\zeta }$
or
![]() $\alpha = \omega ^{\zeta }+1$
for
$\alpha = \omega ^{\zeta }+1$
for
![]() $\zeta \geq 1$
, we associate a countable
$\zeta \geq 1$
, we associate a countable
![]() $X \subset [0,1]$
, such that for
$X \subset [0,1]$
, such that for
![]() $\alpha = \omega ^{\lambda + n}$
, the close-up rank of E is
$\alpha = \omega ^{\lambda + n}$
, the close-up rank of E is
![]() $\lambda + 2n$
, and for
$\lambda + 2n$
, and for
![]() $\alpha = \omega ^{\lambda + n} + 1$
, it is
$\alpha = \omega ^{\lambda + n} + 1$
, it is
![]() $\lambda + 2n + 1$
.
$\lambda + 2n + 1$
.
Let
![]() $\alpha $
be as above and let
$\alpha $
be as above and let
![]() $A = \{0,1,\ldots ,\alpha \}$
with the order topology. As a Von Neumann ordinal,
$A = \{0,1,\ldots ,\alpha \}$
with the order topology. As a Von Neumann ordinal,
![]() $A = \alpha +1$
, but the intended reading of
$A = \alpha +1$
, but the intended reading of
![]() $\phi (A)$
is
$\phi (A)$
is
![]() $\phi (A) = \{\phi (a) \;|\; a \in A\}$
. Take an injective order homomorphism
$\phi (A) = \{\phi (a) \;|\; a \in A\}$
. Take an injective order homomorphism
![]() $\phi : A \to [0,1]$
, so that
$\phi : A \to [0,1]$
, so that
![]() $\phi (0) = 0$
,
$\phi (0) = 0$
,
![]() $\phi (\alpha ) = 1$
. Identify
$\phi (\alpha ) = 1$
. Identify
![]() $0 \equiv 1$
to obtain a continuous function
$0 \equiv 1$
to obtain a continuous function
![]() $\phi : A \to \phi (A) \subset \mathbb {S}^1 = [0,1]/{\equiv }$
, and let
$\phi : A \to \phi (A) \subset \mathbb {S}^1 = [0,1]/{\equiv }$
, and let
![]() $\phi (A) = X$
. The reason for arranging the ordinal on a sphere is simply to compactify the non-compact ordinals, and the reason for wanting non-compact ordinals is to allow the last step of the close-up process to be a transitive closure step.
$\phi (A) = X$
. The reason for arranging the ordinal on a sphere is simply to compactify the non-compact ordinals, and the reason for wanting non-compact ordinals is to allow the last step of the close-up process to be a transitive closure step.
While we do the construction on
![]() $\mathbb {S}^1 = [0,1]/{\equiv }$
rather than
$\mathbb {S}^1 = [0,1]/{\equiv }$
rather than
![]() $[0,1]$
, we note that any non-full closed subset of
$[0,1]$
, we note that any non-full closed subset of
![]() $\mathbb {S}^1$
is homeomorphic to a closed subset of
$\mathbb {S}^1$
is homeomorphic to a closed subset of
![]() $[0,1]$
.
$[0,1]$
.
Let
![]() $E \subset (\mathbb {S}^1)^2$
be the union of the diagonal relation
$E \subset (\mathbb {S}^1)^2$
be the union of the diagonal relation
![]() $\Delta $
and the successor and predecessor relations, that is,
$\Delta $
and the successor and predecessor relations, that is,
Observe that if
![]() $\alpha $
is a successor, we do not join
$\alpha $
is a successor, we do not join
![]() $\phi (\alpha ) = \phi (0)$
with its ‘predecessor’
$\phi (\alpha ) = \phi (0)$
with its ‘predecessor’
![]() $\phi (\alpha -1)$
. It is easy to see that X and E are closed. Consider the close-up process for this relation, starting from
$\phi (\alpha -1)$
. It is easy to see that X and E are closed. Consider the close-up process for this relation, starting from
![]() $E^{(1)} = E$
.
$E^{(1)} = E$
.
Note that at all times,
![]() $E^{(\lambda )}$
for
$E^{(\lambda )}$
for
![]() $\lambda \geq 1$
is symmetric and reflexive, so we simply have to figure out which pairs
$\lambda \geq 1$
is symmetric and reflexive, so we simply have to figure out which pairs
![]() $(\phi (\beta ), \phi (\beta + \gamma ))$
are contained in
$(\phi (\beta ), \phi (\beta + \gamma ))$
are contained in
![]() $E^{(\lambda )}$
for each ordinal
$E^{(\lambda )}$
for each ordinal
![]() $\lambda \geq 1$
. What happens is that only the length of the jumps
$\lambda \geq 1$
. What happens is that only the length of the jumps
![]() $\gamma $
matters. Alternately, we are allowed to first take less than
$\gamma $
matters. Alternately, we are allowed to first take less than
![]() $\omega $
steps with the current relation (a transitive closure step), and then to close up these jumps into a single superjump consisting of
$\omega $
steps with the current relation (a transitive closure step), and then to close up these jumps into a single superjump consisting of
![]() $\omega $
many previous jumps (a topological closure step).
$\omega $
many previous jumps (a topological closure step).
Concretely, we prove an exact characterization of
![]() $E^{(\lambda )}$
by transfinite induction: every ordinal can be written in a unique way as
$E^{(\lambda )}$
by transfinite induction: every ordinal can be written in a unique way as
![]() $\lambda + 2n$
(even ordinals) or
$\lambda + 2n$
(even ordinals) or
![]() $\lambda + 2n + 1$
(odd ordinals) where
$\lambda + 2n + 1$
(odd ordinals) where
![]() $n \in \mathbb {N}$
and
$n \in \mathbb {N}$
and
![]() $\lambda $
is a limit ordinal (interpreting
$\lambda $
is a limit ordinal (interpreting
![]() $0$
as a limit ordinal). For all
$0$
as a limit ordinal). For all
![]() $\lambda , n$
, we prove by induction for all ordinals
$\lambda , n$
, we prove by induction for all ordinals
![]() $\lambda +2n+b$
greater than
$\lambda +2n+b$
greater than
![]() $0$
(
$0$
(
![]() $n \in \mathbb {N}, b \in \{0,1\}$
) that
$n \in \mathbb {N}, b \in \{0,1\}$
) that
The claim for
![]() $E^{(1)}$
is (setting
$E^{(1)}$
is (setting
![]() $\lambda = 0, n = 0, b = 1$
) equivalent to having (up to symmetry)
$\lambda = 0, n = 0, b = 1$
) equivalent to having (up to symmetry)
![]() $E^{(1)} \ni (\beta , \beta +\gamma )$
if and only if
$E^{(1)} \ni (\beta , \beta +\gamma )$
if and only if
![]() $\gamma < 2$
,
$\gamma < 2$
,
![]() $\beta + \gamma < \alpha $
. This is precisely the definition of
$\beta + \gamma < \alpha $
. This is precisely the definition of
![]() $E^{(1)} =~E$
.
$E^{(1)} =~E$
.
For the induction steps, suppose
![]() $E^{(\lambda +2n)}$
is of the claimed form, and consider
$E^{(\lambda +2n)}$
is of the claimed form, and consider
![]() $E^{(\lambda +2n+1)}$
. This is a topological closure step, that is,
$E^{(\lambda +2n+1)}$
. This is a topological closure step, that is,
![]() $E^{(\lambda +2n+1)} = \overline {E^{(\lambda +2n)}}$
. Taking the closure of the pairs given by the inductive assumption, we clearly have
$E^{(\lambda +2n+1)} = \overline {E^{(\lambda +2n)}}$
. Taking the closure of the pairs given by the inductive assumption, we clearly have
If
![]() $\beta> 0$
, then
$\beta> 0$
, then
![]() $(\phi (\beta ), \phi (\beta + \gamma )) \notin E^{(\lambda +2n+1)}$
for
$(\phi (\beta ), \phi (\beta + \gamma )) \notin E^{(\lambda +2n+1)}$
for
![]() $\gamma \geq \omega ^{\lambda + n}+1$
,
$\gamma \geq \omega ^{\lambda + n}+1$
,
![]() $\beta + \gamma < \alpha $
since otherwise
$\beta + \gamma < \alpha $
since otherwise
![]() $(\phi (\theta ), \phi (\beta +\gamma )) \in E^{(\lambda +2n)}$
for
$(\phi (\theta ), \phi (\beta +\gamma )) \in E^{(\lambda +2n)}$
for
![]() $\theta \leq \beta $
arbitrarily close to
$\theta \leq \beta $
arbitrarily close to
![]() $\beta $
and
$\beta $
and
![]() $\gamma \geq \omega ^{\lambda + n}+1$
(note that
$\gamma \geq \omega ^{\lambda + n}+1$
(note that
![]() $\beta + \omega ^{\lambda + n}+1$
is isolated), contradicting the inductive assumption.
$\beta + \omega ^{\lambda + n}+1$
is isolated), contradicting the inductive assumption.
If
![]() $\beta = 0$
, then there may be additional limits on the right end of
$\beta = 0$
, then there may be additional limits on the right end of
![]() $[0,1]/{\equiv }$
. In this case, suppose we have
$[0,1]/{\equiv }$
. In this case, suppose we have
![]() $(\phi (\beta ), \phi (\beta + \gamma )) = (0, \phi (\gamma )) \in E^{(\lambda +2n+1)}$
for
$(\phi (\beta ), \phi (\beta + \gamma )) = (0, \phi (\gamma )) \in E^{(\lambda +2n+1)}$
for
![]() $\omega ^{\lambda + n}+1 \leq \gamma < \alpha $
. To obtain such pairs, we must have
$\omega ^{\lambda + n}+1 \leq \gamma < \alpha $
. To obtain such pairs, we must have
![]() $(\phi (\delta ), \phi (\theta )) \in E^{(\lambda +2n)}$
for
$(\phi (\delta ), \phi (\theta )) \in E^{(\lambda +2n)}$
for
![]() $\theta < \alpha $
arbitrarily close to
$\theta < \alpha $
arbitrarily close to
![]() $\alpha $
and
$\alpha $
and
![]() $\delta \leq \gamma $
arbitrarily close to
$\delta \leq \gamma $
arbitrarily close to
![]() $\gamma $
. If
$\gamma $
. If
![]() $\alpha = \omega ^{\zeta }+1$
, then
$\alpha = \omega ^{\zeta }+1$
, then
![]() $\alpha $
cannot be approximated from below, so this is impossible.
$\alpha $
cannot be approximated from below, so this is impossible.
If
![]() $\alpha = \omega ^{\zeta }$
, then observe that since
$\alpha = \omega ^{\zeta }$
, then observe that since
![]() $\gamma < \alpha $
, we have
$\gamma < \alpha $
, we have
![]() $\omega ^{\lambda + n}+1 \leq \gamma < \alpha $
, so since
$\omega ^{\lambda + n}+1 \leq \gamma < \alpha $
, so since
![]() $\alpha = \omega ^{\zeta }$
, we have
$\alpha = \omega ^{\zeta }$
, we have
![]() $\omega ^{\lambda + n}+1 \leq \gamma \leq \omega ^{\zeta '} \cdot m$
for some
$\omega ^{\lambda + n}+1 \leq \gamma \leq \omega ^{\zeta '} \cdot m$
for some
![]() $\zeta ' < \zeta $
,
$\zeta ' < \zeta $
,
![]() $m \in \mathbb {N}$
(here we simplify the successor and limit case of
$m \in \mathbb {N}$
(here we simplify the successor and limit case of
![]() $\zeta $
into one). Observe that we even have
$\zeta $
into one). Observe that we even have
![]() $\omega ^{\zeta '} \cdot \omega \leq \alpha $
. Now, for any
$\omega ^{\zeta '} \cdot \omega \leq \alpha $
. Now, for any
![]() $\delta \leq \gamma $
and
$\delta \leq \gamma $
and
![]() $\omega ^{\zeta '} \cdot 2m \leq \theta < \alpha $
, we have
$\omega ^{\zeta '} \cdot 2m \leq \theta < \alpha $
, we have
by left distributivity and monotonicity of ordinal multiplication, which means
![]() $(\phi (\delta ), \phi (\theta )) \notin E^{(\lambda +2n)}$
, and thus
$(\phi (\delta ), \phi (\theta )) \notin E^{(\lambda +2n)}$
, and thus
![]() $(\phi (\delta ), \phi (\theta )) \notin \overline {E^{(\lambda +2n)}}$
. This concludes the analysis of the step from
$(\phi (\delta ), \phi (\theta )) \notin \overline {E^{(\lambda +2n)}}$
. This concludes the analysis of the step from
![]() $\lambda +2n$
to
$\lambda +2n$
to
![]() $\lambda +2n+1$
.
$\lambda +2n+1$
.
Suppose then that
![]() $E^{(\lambda +2n+1)}$
is of the claimed form and consider
$E^{(\lambda +2n+1)}$
is of the claimed form and consider
![]() $E^{(\lambda +2n+2)}$
. Since
$E^{(\lambda +2n+2)}$
. Since
![]() $(\phi (\beta ), \phi (\beta + \gamma )) \in E^{(\lambda +2n+1)}$
for all
$(\phi (\beta ), \phi (\beta + \gamma )) \in E^{(\lambda +2n+1)}$
for all
![]() $\beta $
,
$\beta $
,
![]() $\beta + \gamma < \alpha $
with
$\beta + \gamma < \alpha $
with
![]() $\gamma \leq \omega ^{\lambda + n}$
, taking the transitive closure, we have
$\gamma \leq \omega ^{\lambda + n}$
, taking the transitive closure, we have
![]() $(\phi (\beta ), \phi (\beta + \gamma )) \in E^{(\lambda +2n+2)}$
for any
$(\phi (\beta ), \phi (\beta + \gamma )) \in E^{(\lambda +2n+2)}$
for any
![]() $m \in \mathbb {N}$
and
$m \in \mathbb {N}$
and
![]() $\gamma \leq \omega ^{\lambda + n} \cdot m$
with
$\gamma \leq \omega ^{\lambda + n} \cdot m$
with
![]() $\beta + \gamma < \alpha $
. This is indeed equivalent to having
$\beta + \gamma < \alpha $
. This is indeed equivalent to having
![]() $(\phi (\beta ), \phi (\beta + \gamma )) \in E^{(\lambda +2n+2)}$
for any
$(\phi (\beta ), \phi (\beta + \gamma )) \in E^{(\lambda +2n+2)}$
for any
![]() $\gamma < \omega ^{\lambda + n} \cdot \omega = \omega ^{\lambda + n + 1}$
as required.
$\gamma < \omega ^{\lambda + n} \cdot \omega = \omega ^{\lambda + n + 1}$
as required.
To see that
![]() $E^{(\lambda +2n+2)}$
does not contain any pairs
$E^{(\lambda +2n+2)}$
does not contain any pairs
![]() $(\phi (\beta ), \phi (\beta + \gamma ))$
with
$(\phi (\beta ), \phi (\beta + \gamma ))$
with
![]() ${\gamma> \omega ^{\lambda + n} \cdot \omega} $
,
${\gamma> \omega ^{\lambda + n} \cdot \omega} $
,
![]() $\beta + \gamma < \alpha $
, consider any tuple
$\beta + \gamma < \alpha $
, consider any tuple
![]() $(\phi (\beta _1), \phi (\beta _2), \ldots , \phi (\beta _k))$
with
$(\phi (\beta _1), \phi (\beta _2), \ldots , \phi (\beta _k))$
with
![]() $(\phi (\beta _i), \phi (\beta _{i+1})) \in E^{(\lambda +2n+1)}$
,
$(\phi (\beta _i), \phi (\beta _{i+1})) \in E^{(\lambda +2n+1)}$
,
![]() $\beta _i \neq \beta _{i+1}$
for all i, and
$\beta _i \neq \beta _{i+1}$
for all i, and
![]() $\beta _1 < \beta _k$
. If
$\beta _1 < \beta _k$
. If
![]() $\beta _j$
is minimal among of the
$\beta _j$
is minimal among of the
![]() $\beta _i$
, then it easily follows from the inductive assumption that
$\beta _i$
, then it easily follows from the inductive assumption that
This concludes the analysis of the step from
![]() $\lambda +2n+1$
to
$\lambda +2n+1$
to
![]() $\lambda +2n+2$
.
$\lambda +2n+2$
.
Finally, we look at the case where
![]() $\lambda $
is an infinite limit ordinal. By definition,
$\lambda $
is an infinite limit ordinal. By definition,
![]() $E^{(\lambda )} = \bigcup _{\delta < \lambda } E^{(\delta )}$
. We need to show that
$E^{(\lambda )} = \bigcup _{\delta < \lambda } E^{(\delta )}$
. We need to show that
![]() $E^{(\lambda )}$
contains
$E^{(\lambda )}$
contains
![]() $(\phi (\beta ), \phi (\beta +\gamma ))$
for
$(\phi (\beta ), \phi (\beta +\gamma ))$
for
![]() $\beta +\gamma < \alpha $
if and only if
$\beta +\gamma < \alpha $
if and only if
![]() $\gamma < \omega ^{\lambda }$
. Since
$\gamma < \omega ^{\lambda }$
. Since
![]() $\gamma < \omega ^{\lambda }$
is equivalent to
$\gamma < \omega ^{\lambda }$
is equivalent to
![]() $\text { there exists } \delta < \lambda : \gamma < \omega ^{\delta }$
, this follows from the inductive assumption on the relations
$\text { there exists } \delta < \lambda : \gamma < \omega ^{\delta }$
, this follows from the inductive assumption on the relations
![]() $E^{(\delta )}$
. This concludes the analysis of the limit steps.
$E^{(\delta )}$
. This concludes the analysis of the limit steps.
Now observe that by the above characterization,
![]() $E^{(\lambda +2n+b)} = X^2$
if and only if
$E^{(\lambda +2n+b)} = X^2$
if and only if
![]() $(0,\gamma ) \in E^{(\lambda +2n+b)}$
for all
$(0,\gamma ) \in E^{(\lambda +2n+b)}$
for all
![]() $\gamma < \alpha $
. This happens if and only if
$\gamma < \alpha $
. This happens if and only if
![]() $b = 0$
and
$b = 0$
and
![]() $\gamma < \alpha \! \implies \! \gamma < \omega ^{\lambda + n}$
, that is,
$\gamma < \alpha \! \implies \! \gamma < \omega ^{\lambda + n}$
, that is,
![]() $\alpha \leq \omega ^{\lambda + n}$
; or
$\alpha \leq \omega ^{\lambda + n}$
; or
![]() $b = 1$
and
$b = 1$
and
![]() $\gamma < \alpha \!\implies \! \gamma \leq \omega ^{\lambda + n}$
, that is,
$\gamma < \alpha \!\implies \! \gamma \leq \omega ^{\lambda + n}$
, that is,
![]() $\alpha \leq \omega ^{\lambda + n} + 1$
.
$\alpha \leq \omega ^{\lambda + n} + 1$
.
Now, to prove the original claim, for
![]() $\lambda = 1$
, we can realize close-up rank
$\lambda = 1$
, we can realize close-up rank
![]() $1$
by setting
$1$
by setting
![]() $E = X^2$
for any choice of X. For larger countable ordinals, in the above construction, we obtained for the choice
$E = X^2$
for any choice of X. For larger countable ordinals, in the above construction, we obtained for the choice
![]() $\alpha = \omega ^{\lambda + n}$
that the close-up rank of E is
$\alpha = \omega ^{\lambda + n}$
that the close-up rank of E is
![]() $\lambda + 2n$
, and that for the choice
$\lambda + 2n$
, and that for the choice
![]() $\alpha = \omega ^{\lambda + n}+1$
, it is
$\alpha = \omega ^{\lambda + n}+1$
, it is
![]() $\lambda + 2n + 1$
.
$\lambda + 2n + 1$
.
For the last sentence, observe that in the case of odd
![]() $\lambda + 2n + 1$
, the pairs added at the last step are just those joining some
$\lambda + 2n + 1$
, the pairs added at the last step are just those joining some
![]() $\phi (\beta )$
for
$\phi (\beta )$
for
![]() $\beta < \alpha -1$
with
$\beta < \alpha -1$
with
![]() $\phi (\alpha -1)$
. We can realize any such limit through pairs
$\phi (\alpha -1)$
. We can realize any such limit through pairs
![]() $(\phi (\beta ), \phi (\beta _i)) \in E^{(\lambda +2n)}$
, where
$(\phi (\beta ), \phi (\beta _i)) \in E^{(\lambda +2n)}$
, where
![]() $\beta _i \nearrow \alpha -1$
.
$\beta _i \nearrow \alpha -1$
.
Now consider any
![]() $(a_1,\ldots ,a_k,b_1,\ldots ,b_k) \in (E^{[k]})^2$
, where we can take the
$(a_1,\ldots ,a_k,b_1,\ldots ,b_k) \in (E^{[k]})^2$
, where we can take the
![]() $a_i$
to be sorted in increasing order of
$a_i$
to be sorted in increasing order of
![]() $\phi ^{-1}(a_i)$
, and similarly for the
$\phi ^{-1}(a_i)$
, and similarly for the
![]() $b_i$
. If
$b_i$
. If
![]() $(a_1,b_1) \in E^{(\lambda +2n)}$
, then
$(a_1,b_1) \in E^{(\lambda +2n)}$
, then
follows from transitivity of
![]() $E^{(\lambda +2n)}$
. Otherwise, by the above paragraph and up to symmetry, we can assume
$E^{(\lambda +2n)}$
. Otherwise, by the above paragraph and up to symmetry, we can assume
![]() $(a_1, b_1)$
is the limit of
$(a_1, b_1)$
is the limit of
![]() $(\phi (\beta ), \phi (\beta _i))$
. We have
$(\phi (\beta ), \phi (\beta _i))$
. We have
![]() $b_i = b_1$
for all i since
$b_i = b_1$
for all i since
![]() $\phi (\alpha -1)$
is not in E-relation with any other point. We have
$\phi (\alpha -1)$
is not in E-relation with any other point. We have
![]() $a_i \in \{ a_1, \phi (\phi ^{-1}(a_1) + 1) \}$
for all i (recall that the original relation E is just the successor relation, symmetrized and reflexivized), and by the characterization of
$a_i \in \{ a_1, \phi (\phi ^{-1}(a_1) + 1) \}$
for all i (recall that the original relation E is just the successor relation, symmetrized and reflexivized), and by the characterization of
![]() $E^{(\lambda +2n)}$
, we then have
$E^{(\lambda +2n)}$
, we then have
![]() $(a_i, \phi (\beta _i)) \in E^{(\lambda +2n)}$
for any
$(a_i, \phi (\beta _i)) \in E^{(\lambda +2n)}$
for any
![]() $a_i$
, as required.
$a_i$
, as required.
3.2 Spaces as Toeplitz subshifts
See e.g. [Reference Kůrka12] for basic information on Toeplitz subshifts. We recall a basic lemma about Toeplitz subshifts. This is a special case of [Reference Gottschalk and Hedlund7, Theorem 5.23]. (Their term for the formula below is ‘isochronous’, and their term for Toeplitz is ‘regularly almost periodic’.)
Lemma 8. Suppose
![]() $x \in A^{\mathbb {Z}}$
satisfies
$x \in A^{\mathbb {Z}}$
satisfies
 $$ \begin{align*} &\text{ for all } i \in \mathbb{Z}, k> 0: \text{there exists } j \in \mathbb{Z}: \text{there exists } n > 0: \text{for all } \ell \in [-k,k],\\ &\quad m \in \mathbb{Z}: x_{j+\ell+mn} = x_{i+\ell}. \end{align*} $$
$$ \begin{align*} &\text{ for all } i \in \mathbb{Z}, k> 0: \text{there exists } j \in \mathbb{Z}: \text{there exists } n > 0: \text{for all } \ell \in [-k,k],\\ &\quad m \in \mathbb{Z}: x_{j+\ell+mn} = x_{i+\ell}. \end{align*} $$
Then
![]() $\overline {O(x)}$
is Toeplitz.
$\overline {O(x)}$
is Toeplitz.
In words, the assumption is that every subword appearing in x at i appears in some arithmetic progression in x (but not necessarily one going through position i).
Proof. We need to show that the orbit-closure of x contains a Toeplitz point with the same language as x. Let
![]() $w_1 = x|_{[-1,1]}$
and let
$w_1 = x|_{[-1,1]}$
and let
![]() $j_1$
be such that an arithmetic progression of
$j_1$
be such that an arithmetic progression of
![]() $w_1$
s with difference
$w_1$
s with difference
![]() $n_1$
begins at
$n_1$
begins at
![]() $j_1$
. Replace x by
$j_1$
. Replace x by
![]() $x^1 = \sigma ^{j_1}(x)$
, so that we still have
$x^1 = \sigma ^{j_1}(x)$
, so that we still have
![]() $w_1 = x^1|_{[-1,1]}$
, but now the central three coordinates are in an arithmetic progression. From now on, restrict to shifting by multiples of
$w_1 = x^1|_{[-1,1]}$
, but now the central three coordinates are in an arithmetic progression. From now on, restrict to shifting by multiples of
![]() $n_1$
.
$n_1$
.
By the original assumption, the central word
![]() $x^1|_{[-n_1-|j_1|-2, n_1+|j_1|+2]}$
is in an arithmetic progression beginning at some
$x^1|_{[-n_1-|j_1|-2, n_1+|j_1|+2]}$
is in an arithmetic progression beginning at some
![]() $j_2$
with difference
$j_2$
with difference
![]() $n_2$
, we may take
$n_2$
, we may take
![]() $n_1 \;|\; n_2$
. Let
$n_1 \;|\; n_2$
. Let
![]() $x^2 = \sigma ^{h_2 n_1}(x^1)$
, where
$x^2 = \sigma ^{h_2 n_1}(x^1)$
, where
![]() and where
and where
![]() denotes integer division discarding remainder. Since we shifted by a multiple of
denotes integer division discarding remainder. Since we shifted by a multiple of
![]() $n_1$
, in
$n_1$
, in
![]() $x^2$
, the word at
$x^2$
, the word at
![]() $[-1,1]$
still lies in an arithmetic progression with difference
$[-1,1]$
still lies in an arithmetic progression with difference
![]() $n_1$
. However, since we shifted by a number with distance at most
$n_1$
. However, since we shifted by a number with distance at most
![]() $n_1$
from
$n_1$
from
![]() $j_2$
, now the subword
$j_2$
, now the subword
![]() $x^2|_{[-2-|j_1|, 2+|j_1|]}$
lies in an arithmetic progression with difference
$x^2|_{[-2-|j_1|, 2+|j_1|]}$
lies in an arithmetic progression with difference
![]() $n_2$
. Observe that this contains the word
$n_2$
. Observe that this contains the word
![]() $x|_{[-2, 2]}$
.
$x|_{[-2, 2]}$
.
In
![]() $x^2$
, we have inserted Toeplitz periods for more coordinates, without modifying the periods we already introduced for
$x^2$
, we have inserted Toeplitz periods for more coordinates, without modifying the periods we already introduced for
![]() $x^1$
, and also introduced larger subwords of x into the periodic area. An obvious induction gives a Toeplitz point with the same language as that of x in the limit.
$x^1$
, and also introduced larger subwords of x into the periodic area. An obvious induction gives a Toeplitz point with the same language as that of x in the limit.
The positioned words over A are
![]() $A^{**} = \{w : [a,b] \to A \;|\; a,b \in \mathbb {Z} \}$
, formally the same as finite words, but we do not identify them up to translations. For
$A^{**} = \{w : [a,b] \to A \;|\; a,b \in \mathbb {Z} \}$
, formally the same as finite words, but we do not identify them up to translations. For
![]() ${w \in A^{**}}$
,
${w \in A^{**}}$
,
![]() $w :$
$w :$
![]() $[a,b] \to A$
, and
$[a,b] \to A$
, and
![]() $X \subset A^{\mathbb {Z}}$
a subshift (deduced from context), write
$X \subset A^{\mathbb {Z}}$
a subshift (deduced from context), write
![]() $[w] = \{x \in X \;|\; x|_{[a,b]} = w\}$
.
$[w] = \{x \in X \;|\; x|_{[a,b]} = w\}$
.
Lemma 4. For any compact metrizable zero-dimensional space Z, there exists a pointwise zero-entropy Toeplitz subshift X and an open quotient map
![]() $\phi : X \to Z$
such that
$\phi : X \to Z$
such that
![]() $\phi ^{-1}(z)$
is a minimal subshift for every
$\phi ^{-1}(z)$
is a minimal subshift for every
![]() $z \in Z$
, and
$z \in Z$
, and
![]() $\phi $
induces a homeomorphism between Z and the space of minimal subshifts of X.
$\phi $
induces a homeomorphism between Z and the space of minimal subshifts of X.
Proof. Define the subshift
![]() $X' \subset \{0,1,\#\}^{\mathbb {Z}}$
by requiring that in every point, there is an arithmetic progression
$X' \subset \{0,1,\#\}^{\mathbb {Z}}$
by requiring that in every point, there is an arithmetic progression
![]() $\{3k+i \;|\; k \in \mathbb {Z}\}$
containing only
$\{3k+i \;|\; k \in \mathbb {Z}\}$
containing only
![]() $\#$
, such that
$\#$
, such that
![]() $\{3k+i+1 \;|\; k \in \mathbb {Z}\}$
is a constant sequence containing only
$\{3k+i+1 \;|\; k \in \mathbb {Z}\}$
is a constant sequence containing only
![]() $0$
or only
$0$
or only
![]() $1$
, and recursively
$1$
, and recursively
![]() $\{3k+i+2 \;|\; k \in \mathbb {Z}\}$
is a point of
$\{3k+i+2 \;|\; k \in \mathbb {Z}\}$
is a point of
![]() $X'$
.
$X'$
.
This indeed describes a unique subshift whose typical points look like
where
![]() $z \in \{0,1\}^{\mathbb {N}}$
, and we associate a sequence of bits to every point in
$z \in \{0,1\}^{\mathbb {N}}$
, and we associate a sequence of bits to every point in
![]() $X'$
by locating the unique infinite
$X'$
by locating the unique infinite
![]() $3$
-progression of
$3$
-progression of
![]() $\#$
s (which can be deduced from any word of length
$\#$
s (which can be deduced from any word of length
![]() $3$
), outputting the bit to the right of one (thus any) of them, and recursively extracting the rest of the bits from the third
$3$
), outputting the bit to the right of one (thus any) of them, and recursively extracting the rest of the bits from the third
![]() $3$
-progression. Let
$3$
-progression. Let
![]() $\phi : X' \to \{0,1\}^{\mathbb {N}}$
extract this sequence of bits, so
$\phi : X' \to \{0,1\}^{\mathbb {N}}$
extract this sequence of bits, so
![]() $\phi $
is continuous, and
$\phi $
is continuous, and
![]() $\phi (x) = \phi (\sigma (x))$
for all
$\phi (x) = \phi (\sigma (x))$
for all
![]() $x \in X'$
.
$x \in X'$
.
Since Z is compact, metrizable, and zero-dimensional, we can take (up to homeomorphism)
![]() $Z \subset \{0,1\}^{\mathbb {N}}$
a closed set such that no point in Z is eventually constant, equivalently,
$Z \subset \{0,1\}^{\mathbb {N}}$
a closed set such that no point in Z is eventually constant, equivalently,
![]() $01$
appears infinitely many times in every
$01$
appears infinitely many times in every
![]() $z \in Z$
. Define
$z \in Z$
. Define
![]() $X = \phi ^{-1}(Z)$
, which is clearly a subshift. A simple computation shows that the number of words of length n in X (even in
$X = \phi ^{-1}(Z)$
, which is clearly a subshift. A simple computation shows that the number of words of length n in X (even in
![]() $X'$
) is
$X'$
) is
![]() $O(n^{\log _3 6})$
, so X has zero entropy.
$O(n^{\log _3 6})$
, so X has zero entropy.
The map
![]() $\phi $
is surjective and continuous by definition, and it is closed since X is compact and Z Hausdorff, so it is a quotient map from X to Z.
$\phi $
is surjective and continuous by definition, and it is closed since X is compact and Z Hausdorff, so it is a quotient map from X to Z.
Let us now analyze the dynamical structure of Z. Call the unique infinite
![]() $3$
-progression of
$3$
-progression of
![]() $\#$
s in a point of X the
$\#$
s in a point of X the
![]() $0$
-skeleton. Recursively, we refer to the
$0$
-skeleton. Recursively, we refer to the
![]() $0$
-skeleton of the point of
$0$
-skeleton of the point of
![]() $X'$
obtained after i iterations of the recursive extraction process as the i-skeleton. The skeleton refers collectively to the family of all the i-skeletons, more precisely, the skeleton of
$X'$
obtained after i iterations of the recursive extraction process as the i-skeleton. The skeleton refers collectively to the family of all the i-skeletons, more precisely, the skeleton of
![]() $x \in X$
is
$x \in X$
is
![]() $\pi (x)$
, where
$\pi (x)$
, where
![]() $\pi (\#) = \#$
,
$\pi (\#) = \#$
,
![]() $\pi (0) = \pi (1) = 0$
.
$\pi (0) = \pi (1) = 0$
.
Dynamically, extraction of the skeletons gives an almost-one-to-one subshift cover of the
![]() $3$
-odometer
$3$
-odometer
![]() $(\mathbb {Z}_3, (a \mapsto a+1))$
(where
$(\mathbb {Z}_3, (a \mapsto a+1))$
(where
![]() $\mathbb {Z}_3$
is the space of
$\mathbb {Z}_3$
is the space of
![]() $3$
-adic integers), more precisely,
$3$
-adic integers), more precisely,
![]() $\pi (X)$
is a two-to-one, and almost one-to-one, cover of the
$\pi (X)$
is a two-to-one, and almost one-to-one, cover of the
![]() $3$
-odometer, by the obvious map
$3$
-odometer, by the obvious map
![]() $\psi : \pi (X) \to \mathbb {Z}_3$
that records the offsets of the
$\psi : \pi (X) \to \mathbb {Z}_3$
that records the offsets of the
![]() $\#$
-progressions in an intertwining way. What happens is that a typical
$\#$
-progressions in an intertwining way. What happens is that a typical
![]() $\psi (\pi (x))$
determines the skeleton
$\psi (\pi (x))$
determines the skeleton
![]() $\pi (x)$
entirely. If it does not, then there is a single ‘hole’ left after filling in the
$\pi (x)$
entirely. If it does not, then there is a single ‘hole’ left after filling in the
![]() $\#$
s. If there is a hole left, then
$\#$
s. If there is a hole left, then
![]() $|\psi ^{-1}(\psi (\pi (x)))| = 2$
.
$|\psi ^{-1}(\psi (\pi (x)))| = 2$
.
It is easy to see that if
![]() $\psi ^{-1}(\psi (\pi (x)))$
is a singleton, then for any
$\psi ^{-1}(\psi (\pi (x)))$
is a singleton, then for any
![]() $z \in Z$
, there is exactly one point
$z \in Z$
, there is exactly one point
![]() $x' \in X$
with
$x' \in X$
with
![]() $\phi (x') = z$
and
$\phi (x') = z$
and
![]() $\pi (x') = \pi (x)$
, since after filling in the skeleton and the bits to the right of it, there is no hole left to insert a
$\pi (x') = \pi (x)$
, since after filling in the skeleton and the bits to the right of it, there is no hole left to insert a
![]() $\#$
, thus no hole to insert a bit either. If there is a hole left, then we can insert any of
$\#$
, thus no hole to insert a bit either. If there is a hole left, then we can insert any of
![]() $0,1,\#$
, but all other cells are determined by
$0,1,\#$
, but all other cells are determined by
![]() $\psi (\pi (x))$
and
$\psi (\pi (x))$
and
![]() $\phi (x)$
.
$\phi (x)$
.
It follows that the subshift X itself is a three-to-one and almost-one-to-one subshift cover of the system
![]() $\mathbb {Z}_3 \times Z$
under
$\mathbb {Z}_3 \times Z$
under
![]() $(\alpha , z) \mapsto (\alpha +1, z)$
, where
$(\alpha , z) \mapsto (\alpha +1, z)$
, where
![]() $\mathbb {Z}_3$
denotes the
$\mathbb {Z}_3$
denotes the
![]() $3$
-odometer.
$3$
-odometer.
We now show the openness of
![]() $\phi $
. Suppose
$\phi $
. Suppose
![]() $x \in [u]$
and
$x \in [u]$
and
![]() $\phi (x) = z$
. Pick
$\phi (x) = z$
. Pick
![]() $x' \in [u]$
such that
$x' \in [u]$
such that
![]() $\phi (x') = z$
and
$\phi (x') = z$
and
This is possible because
![]() $[u]$
determines only part of the skeleton of x, and we may modify the rest to find
$[u]$
determines only part of the skeleton of x, and we may modify the rest to find
![]() $x'$
such that
$x'$
such that
![]() $\pi (x')$
is a singleton
$\pi (x')$
is a singleton
![]() $\psi $
-fiber. The bits left in u after determining part of the skeleton do not constrain this since there are no eventually constant points in Z; that is, if there is a hole left in x after determining the skeleton and filling in the bits of z, and this hole is filled with
$\psi $
-fiber. The bits left in u after determining part of the skeleton do not constrain this since there are no eventually constant points in Z; that is, if there is a hole left in x after determining the skeleton and filling in the bits of z, and this hole is filled with
![]() $a \in \{0,1,\#\}$
, then we can pick
$a \in \{0,1,\#\}$
, then we can pick
![]() $x'$
so that this hole is filled with a, at the point of the process where a suitable bit emerges.
$x'$
so that this hole is filled with a, at the point of the process where a suitable bit emerges.
Now pick
![]() $w \in \{0,1\}^{*}$
, with
$w \in \{0,1\}^{*}$
, with
![]() $z \in [w]$
, long enough so the bits in u are determined by those in w (when using the skeleton of
$z \in [w]$
, long enough so the bits in u are determined by those in w (when using the skeleton of
![]() $x'$
), so that for all
$x'$
), so that for all
![]() $z' \in [w]$
, there exists a (unique) point
$z' \in [w]$
, there exists a (unique) point
![]() $y \in [u]$
with
$y \in [u]$
with
![]() $\pi (y) = \pi (x') \wedge \phi (y) = z'$
. This means
$\pi (y) = \pi (x') \wedge \phi (y) = z'$
. This means
![]() $\phi ([u]) \supset [w] \ni z$
. Thus
$\phi ([u]) \supset [w] \ni z$
. Thus
![]() $\phi $
is open.
$\phi $
is open.
To see that every point generates a Toeplitz subshift, let
![]() $x \in X$
be arbitrary and suppose
$x \in X$
be arbitrary and suppose
![]() $x \in [u]$
for some
$x \in [u]$
for some
![]() $u \in A^{**}$
,
$u \in A^{**}$
,
![]() $u : [a,b] \to A$
. If
$u : [a,b] \to A$
. If
![]() $\psi ^{-1}(\psi (\pi (x)))$
is a singleton, that is,
$\psi ^{-1}(\psi (\pi (x)))$
is a singleton, that is,
![]() $\pi (x)$
and
$\pi (x)$
and
![]() $\phi (x)$
determine x uniquely, then clearly there exists a period
$\phi (x)$
determine x uniquely, then clearly there exists a period
![]() $3^n> 0$
such that
$3^n> 0$
such that
![]() $\sigma ^{i3^n}(x) \in [u]$
for all
$\sigma ^{i3^n}(x) \in [u]$
for all
![]() $i \in \mathbb {Z}$
, that is, x is already Toeplitz. In general, it suffices to show the condition from the previous lemma, so we show that the word u appears in some arithmetic progression in x.
$i \in \mathbb {Z}$
, that is, x is already Toeplitz. In general, it suffices to show the condition from the previous lemma, so we show that the word u appears in some arithmetic progression in x.
For this, note that since
![]() $\pi (X)$
is an almost-one-to-one cover of
$\pi (X)$
is an almost-one-to-one cover of
![]() $\mathbb {Z}_3$
and
$\mathbb {Z}_3$
and
![]() $\mathbb {Z}_3$
is minimal, we can find j such that the set
$\mathbb {Z}_3$
is minimal, we can find j such that the set
![]() $\psi ^{-1}(\psi (\pi (\sigma ^j(x))))$
has very small diameter. In particular, we can ensure that the symbols in
$\psi ^{-1}(\psi (\pi (\sigma ^j(x))))$
has very small diameter. In particular, we can ensure that the symbols in
![]() $\pi (x)_{[a,b]}$
are uniquely determined by
$\pi (x)_{[a,b]}$
are uniquely determined by
![]() $\psi (\pi (\sigma ^j(x)))$
. It follows (as discussed in the proof) that the skeleton
$\psi (\pi (\sigma ^j(x)))$
. It follows (as discussed in the proof) that the skeleton
![]() $\psi (\pi (\sigma ^j(x)))$
and finitely many bits in
$\psi (\pi (\sigma ^j(x)))$
and finitely many bits in
![]() $\phi (x)$
actually determine the word
$\phi (x)$
actually determine the word
![]() $\sigma ^j(x)_{[a,b]}$
uniquely. Since
$\sigma ^j(x)_{[a,b]}$
uniquely. Since
![]() $\phi (x)$
is not eventually constant, we can pick j so that together with the bits of z, the forced word is
$\phi (x)$
is not eventually constant, we can pick j so that together with the bits of z, the forced word is
![]() $\sigma ^j(x)_{[a, b]} = u$
. The subword
$\sigma ^j(x)_{[a, b]} = u$
. The subword
![]() $[j+a, j+b]$
of x then appears in an arithmetic progression because of the equicontinuity properties of the
$[j+a, j+b]$
of x then appears in an arithmetic progression because of the equicontinuity properties of the
![]() $3$
-odometer, as required.
$3$
-odometer, as required.
Observe now that (since every Toeplitz subshift is minimal) every point generates a minimal subshift, and this subshift maps to a single point in
![]() $\phi $
. Conversely, the language of a minimal subshift is determined by the bits in its image in a continuous way (again use that no point in Z is eventually constant). Thus the fibers of
$\phi $
. Conversely, the language of a minimal subshift is determined by the bits in its image in a continuous way (again use that no point in Z is eventually constant). Thus the fibers of
![]() $\phi $
are precisely the minimal subshifts of X and
$\phi $
are precisely the minimal subshifts of X and
![]() $\phi $
induces a homeomorphism between them and Z.
$\phi $
induces a homeomorphism between them and Z.
3.3 Relations as entropy pairs
Next, we realize relations as entropy pairs. We first deal with the easy case where E is not doubly shift-invariant, but we only realize the relation, not the whole process. We prove this statement as it sounds nicer than the technical result we actually need, and illustrates some of the ideas used in the following section. However, it is not used in the construction of CPE ranks.
For
![]() $y \in A^{\mathbb {Z}}$
, write
$y \in A^{\mathbb {Z}}$
, write
![]() $w \sqsubset y\! \iff \text {there exists } i: y_{[i,i+|w|-1]} = w$
, and for
$w \sqsubset y\! \iff \text {there exists } i: y_{[i,i+|w|-1]} = w$
, and for
![]() $Y \subset A^{\mathbb {Z}}$
, write
$Y \subset A^{\mathbb {Z}}$
, write
![]() $w \sqsubset Y \! \iff \text {there exists } y \in Y: w \sqsubset y$
.
$w \sqsubset Y \! \iff \text {there exists } y \in Y: w \sqsubset y$
.
Proposition 6. Suppose X has zero entropy and
![]() $E \subset X^2$
is a closed symmetric reflexive shift-invariant relation. Then there exists a subshift Y with
$E \subset X^2$
is a closed symmetric reflexive shift-invariant relation. Then there exists a subshift Y with
![]() $X \subset Y \subset \hat A^{\mathbb {Z}}$
(over a possibly larger alphabet
$X \subset Y \subset \hat A^{\mathbb {Z}}$
(over a possibly larger alphabet
![]() $\hat A \supset A$
) such that
$\hat A \supset A$
) such that
![]() $\mathrm {EP}(Y) \cap X^2 = E$
.
$\mathrm {EP}(Y) \cap X^2 = E$
.
Proof. Let
![]() $\hat A = A \cup \{\#\}$
, fix a sequence
$\hat A = A \cup \{\#\}$
, fix a sequence
![]() $(x^n, y^n) \in E$
such that each pair
$(x^n, y^n) \in E$
such that each pair
![]() $(x, y) \in E$
is a limit point of the sequence, and define
$(x, y) \in E$
is a limit point of the sequence, and define
(that is,
![]() $Y_n$
is the shift-invariant set of all points of the stated form). Let
$Y_n$
is the shift-invariant set of all points of the stated form). Let
![]() $Y = \overline {\bigcup _{n} Y_n}$
.
$Y = \overline {\bigcup _{n} Y_n}$
.
If
![]() $(x,y) \in E \setminus \Delta $
, then obviously by picking larger and larger n such that
$(x,y) \in E \setminus \Delta $
, then obviously by picking larger and larger n such that
![]() $(x^n, y^n)$
is very close to
$(x^n, y^n)$
is very close to
![]() $(x,y)$
,
$(x,y)$
,
![]() $Y_n \subset Y$
implies that
$Y_n \subset Y$
implies that
![]() $(x,y) \in \mathrm {EP}(Y)$
. (This is obvious from the intuition stated in the introduction: even if we only obtain information when the orbit is very close to x and y, we obtain an exponential amount of information from points of
$(x,y) \in \mathrm {EP}(Y)$
. (This is obvious from the intuition stated in the introduction: even if we only obtain information when the orbit is very close to x and y, we obtain an exponential amount of information from points of
![]() $Y_n$
if
$Y_n$
if
![]() $d((x_n, y_n), (x, y))$
is very small. The concrete computation is also straightforward.)
$d((x_n, y_n), (x, y))$
is very small. The concrete computation is also straightforward.)
Suppose then that
![]() $(x,y) \in X^2 \setminus E$
. Since E is closed, for some n, we have
$(x,y) \in X^2 \setminus E$
. Since E is closed, for some n, we have
![]() $([x_{[-k,k]}] \times [y_{[-k,k]}]) \cap E = \emptyset $
. We claim that for
$([x_{[-k,k]}] \times [y_{[-k,k]}]) \cap E = \emptyset $
. We claim that for
![]() $U = [x_{[-k,k]}], V = [y_{[-k,k]}]$
, the cover
$U = [x_{[-k,k]}], V = [y_{[-k,k]}]$
, the cover
![]() $(C_0, C_1) = (U^c, V^c)$
has zero topological entropy. By definition, to show this, we must give for each m, a set of binary words
$(C_0, C_1) = (U^c, V^c)$
has zero topological entropy. By definition, to show this, we must give for each m, a set of binary words
![]() $W \subset \{0,1\}^m$
, whose size grows subexponentially in m, such that for any
$W \subset \{0,1\}^m$
, whose size grows subexponentially in m, such that for any
![]() $z \in Y$
, there exists
$z \in Y$
, there exists
![]() $w \in W$
such that
$w \in W$
such that
![]() $\sigma ^i(z) \in C_{w_i}$
for all
$\sigma ^i(z) \in C_{w_i}$
for all
![]() $i \in \{0,1, 2,\ldots , m-1\}$
. In other words, we must cover all partial orbits of length m with a subexponential (in m) number of sets of the form
$i \in \{0,1, 2,\ldots , m-1\}$
. In other words, we must cover all partial orbits of length m with a subexponential (in m) number of sets of the form
![]() $\bigcap _{i = 0}^{m-1} \sigma ^{-i}(C_{w_i})$
.
$\bigcap _{i = 0}^{m-1} \sigma ^{-i}(C_{w_i})$
.
Since the sets
![]() $C_i$
are clopen, we can equivalently consider a covering problem for words, that is, it is sufficient to find a set of binary words
$C_i$
are clopen, we can equivalently consider a covering problem for words, that is, it is sufficient to find a set of binary words
![]() $W \subset \{0,1\}^m$
such that for each
$W \subset \{0,1\}^m$
such that for each
![]() $t \in \mathcal {L}_m(Y)$
, there exists
$t \in \mathcal {L}_m(Y)$
, there exists
![]() $w \in W$
such that
$w \in W$
such that
![]() $(U^c, V^c)^w$
intersects
$(U^c, V^c)^w$
intersects
![]() $[t]$
, where
$[t]$
, where
![]() $(U^c, V^c)^u$
is defined inductively on word length by
$(U^c, V^c)^u$
is defined inductively on word length by
for
![]() $a \in \{0,1\}, w \in \{0,1\}^m$
. In fact, we need at most
$a \in \{0,1\}, w \in \{0,1\}^m$
. In fact, we need at most
![]() $(|A|+1)^{2k}$
times more sets to cover the partial orbits than for this covering problem for words, and this constant factor is subsumed by subexponential growth. Let us say
$(|A|+1)^{2k}$
times more sets to cover the partial orbits than for this covering problem for words, and this constant factor is subsumed by subexponential growth. Let us say
![]() $w \in \{0,1\}^m$
covers
$w \in \{0,1\}^m$
covers
![]() $t \sqsubset \mathcal {L}_m(Y)$
if
$t \sqsubset \mathcal {L}_m(Y)$
if
![]() $(U^c, V^c)^w \cap [t] \neq \emptyset $
.
$(U^c, V^c)^w \cap [t] \neq \emptyset $
.
We first note that the words t containing at most one
![]() $\#$
are easy to cover. For such
$\#$
are easy to cover. For such
![]() $t \sqsubset Y$
, we always have
$t \sqsubset Y$
, we always have
![]() $t \sqsubset X$
or
$t \sqsubset X$
or
![]() $t = u\#v$
, where u and v are words in X. All such words appear in a morphic image of the zero entropy subshift
$t = u\#v$
, where u and v are words in X. All such words appear in a morphic image of the zero entropy subshift
![]() $X^2 \times \overline {\mathcal {O}(\ldots 000111\ldots )}$
, so they cannot generate entropy with respect to any cover. More concretely, letting
$X^2 \times \overline {\mathcal {O}(\ldots 000111\ldots )}$
, so they cannot generate entropy with respect to any cover. More concretely, letting
![]() $f(m)$
be the number of words of length m in X, the number of words of length m of the forms
$f(m)$
be the number of words of length m in X, the number of words of length m of the forms
![]() $t \sqsubset X$
or
$t \sqsubset X$
or
![]() $u \# v$
, where
$u \# v$
, where
![]() $u,v \sqsubset X$
, is at most
$u,v \sqsubset X$
, is at most
![]() $f(m) + \sum _{i = 0}^m f(i) f(m-i-1)$
. If f grows subexponentially, its self-convolution grows subexponentially as well. Thus for each word of these two forms, we can simply include an arbitrary covering word in W.
$f(m) + \sum _{i = 0}^m f(i) f(m-i-1)$
. If f grows subexponentially, its self-convolution grows subexponentially as well. Thus for each word of these two forms, we can simply include an arbitrary covering word in W.
To cover words with at least two
![]() $\#$
-symbols, observe that in Y, all such words have an arithmetic progression of
$\#$
-symbols, observe that in Y, all such words have an arithmetic progression of
![]() $\#$
s. Consider a progression
$\#$
s. Consider a progression
![]() $\alpha = \{i(2n+2) + c \;|\; i \in \mathbb {Z}\} \cap \{0,1, 2,\ldots , m-1\}$
, where
$\alpha = \{i(2n+2) + c \;|\; i \in \mathbb {Z}\} \cap \{0,1, 2,\ldots , m-1\}$
, where
![]() $n \geq 0, c \in [0,2n+1]$
and
$n \geq 0, c \in [0,2n+1]$
and
![]() $|\alpha | \geq 2$
. Then the set of words where
$|\alpha | \geq 2$
. Then the set of words where
![]() $\#$
s appear exactly in this arithmetic progression consists precisely of words obtained by inserting any combination of
$\#$
s appear exactly in this arithmetic progression consists precisely of words obtained by inserting any combination of
![]() $x^n_{[-n,n]}$
or
$x^n_{[-n,n]}$
or
![]() $y^n_{[-n,n]}$
between
$y^n_{[-n,n]}$
between
![]() $i(2n+2) + c$
and
$i(2n+2) + c$
and
![]() $(i+1)$
$(i+1)$
![]() $(2n+2) + c$
for each i (and we have up to four choices in total for the prefix and suffix).
$(2n+2) + c$
for each i (and we have up to four choices in total for the prefix and suffix).
Since
![]() $(x^n,y^n) \in E$
, by shift-invariance also
$(x^n,y^n) \in E$
, by shift-invariance also
![]() $(\sigma ^\ell (x^n), \sigma ^\ell (y^n)) \in E$
for all
$(\sigma ^\ell (x^n), \sigma ^\ell (y^n)) \in E$
for all
![]() $\ell \in \mathbb {Z}$
and thus from
$\ell \in \mathbb {Z}$
and thus from
![]() $([x_{[-k,k]}] \times [y_{[-k,k]}]) \cap E = \emptyset $
, we obtain that for all
$([x_{[-k,k]}] \times [y_{[-k,k]}]) \cap E = \emptyset $
, we obtain that for all
![]() $\ell $
,
$\ell $
,
and thus see that there is a single word
![]() $w_{n,c}$
of length m that covers every word t with progression
$w_{n,c}$
of length m that covers every word t with progression
![]() $\alpha $
. This gives a polynomial bound on the number of words w needed to cover those t with at least two
$\alpha $
. This gives a polynomial bound on the number of words w needed to cover those t with at least two
![]() $\#$
s, all in all, we have obtained a subexponential bound.
$\#$
s, all in all, we have obtained a subexponential bound.
3.4 Doubly invariant relations as entropy pairs
Lemma 5. Let
![]() $X \subset A^{\mathbb {Z}}$
be a subshift with zero entropy and let
$X \subset A^{\mathbb {Z}}$
be a subshift with zero entropy and let
![]() $E \subset X^2$
be a closed doubly shift-invariant symmetric reflexive relation. Then there exists a subshift Y with
$E \subset X^2$
be a closed doubly shift-invariant symmetric reflexive relation. Then there exists a subshift Y with
![]() $X \subset Y \subset \hat A^{\mathbb {Z}}$
(over a possibly larger alphabet
$X \subset Y \subset \hat A^{\mathbb {Z}}$
(over a possibly larger alphabet
![]() $\hat A \supset A$
) such that
$\hat A \supset A$
) such that
![]() $\mathrm {EP}(Y)^{(\lambda )} \cap X^2 = E^{(\lambda )}$
for all
$\mathrm {EP}(Y)^{(\lambda )} \cap X^2 = E^{(\lambda )}$
for all
![]() $\lambda $
. Furthermore, if
$\lambda $
. Furthermore, if
![]() $E^{(\lambda )} \cap X^2 = X^2$
, then
$E^{(\lambda )} \cap X^2 = X^2$
, then
![]() $\mathrm {EP}(Y)^{(\lambda +1)} = Y^2$
, and we have
$\mathrm {EP}(Y)^{(\lambda +1)} = Y^2$
, and we have
![]() $\mathrm {EP}(Y)^{(\lambda )} = Y^2$
if:
$\mathrm {EP}(Y)^{(\lambda )} = Y^2$
if:
-
•
 $\lambda $
is even; or
$\lambda $
is even; or -
•
 $\lambda $
is odd and
$\lambda $
is odd and
 $(E^{[k]})^2 \subset \overline {(E^{(\lambda -1)})^{[2k]} \cap (E^{[k]})^2}$
.
$(E^{[k]})^2 \subset \overline {(E^{(\lambda -1)})^{[2k]} \cap (E^{[k]})^2}$
.
Proof. Define
![]() $w_0 = 1$
and inductively
$w_0 = 1$
and inductively
![]() $w_{i+1} = w_i 0^{i+1} w_i$
. Define
$w_{i+1} = w_i 0^{i+1} w_i$
. Define
Another description is that
![]() $w_\omega $
is obtained from the ruler sequence A007814 in OEIS [13] or universal counterexample [Reference Ferenczi6]
$w_\omega $
is obtained from the ruler sequence A007814 in OEIS [13] or universal counterexample [Reference Ferenczi6]
by applying the substitution
![]() $n \mapsto 10^{n+1}$
(or
$n \mapsto 10^{n+1}$
(or
![]() $0 \mapsto 1$
,
$0 \mapsto 1$
,
![]() $n \mapsto 0^{n}$
). We refer to the words
$n \mapsto 0^{n}$
). We refer to the words
![]() $w_i$
and their obvious positioned variants as full words and refer to the process of extending a positioned
$w_i$
and their obvious positioned variants as full words and refer to the process of extending a positioned
![]() $w_i \in A^{**}$
to
$w_i \in A^{**}$
to
![]() $w_{i+1} \in A^{**}$
(which can be done in exactly two ways) as the left or right full extension.
$w_{i+1} \in A^{**}$
(which can be done in exactly two ways) as the left or right full extension.
By induction
![]() $n_i = |w_i| = 3 \cdot 2^i - i - 2$
and
$n_i = |w_i| = 3 \cdot 2^i - i - 2$
and
![]() $\sum _j (w_i)_j = 2^i$
. A short computation shows that for every
$\sum _j (w_i)_j = 2^i$
. A short computation shows that for every
![]() $k \geq 1$
, there exists a subword of
$k \geq 1$
, there exists a subword of
![]() $w_\omega $
of length k (for example its prefix), where the symbol
$w_\omega $
of length k (for example its prefix), where the symbol
![]() $1$
appears at least
$1$
appears at least
![]() $k/3$
times (any
$k/3$
times (any
![]() $k/c$
works just as well for what follows).
$k/c$
works just as well for what follows).
We now perform some substitutions to obtain a subshift. Let
![]() $\tau (0) = \{0\}, \tau (1) = \{1, 11\}$
be a non-deterministic substitution and define
$\tau (0) = \{0\}, \tau (1) = \{1, 11\}$
be a non-deterministic substitution and define
![]() $Y''' = \tau (w_\omega ) \subset \{0,1\}^{\mathbb {N}}$
, that is,
$Y''' = \tau (w_\omega ) \subset \{0,1\}^{\mathbb {N}}$
, that is,
![]() $Y'''$
is the set of all possible points obtained by replacing
$Y'''$
is the set of all possible points obtained by replacing
![]() $0$
s in
$0$
s in
![]() $w_\omega $
by
$w_\omega $
by
![]() $0$
s, and
$0$
s, and
![]() $1$
s by either
$1$
s by either
![]() $1$
or
$1$
or
![]() $11$
. Let
$11$
. Let
![]() $\hat A = A \sqcup \{\#\}$
where
$\hat A = A \sqcup \{\#\}$
where
![]() $\# \notin A$
, and let
$\# \notin A$
, and let
![]() $\tau ' : \hat A \to \{0,1\}$
be the deterministic substitution mapping
$\tau ' : \hat A \to \{0,1\}$
be the deterministic substitution mapping
![]() $\# \mapsto 1$
and
$\# \mapsto 1$
and
![]() $a \mapsto 0$
for
$a \mapsto 0$
for
![]() $a \in A$
. Let
$a \in A$
. Let
![]() $Y'' = (\tau ')^{-1}(Y''')$
. Let
$Y'' = (\tau ')^{-1}(Y''')$
. Let
![]() $Y'$
be the
$Y'$
be the
![]() $\mathbb {Z}$
-subshift whose language consists of the left-extendable words in the language of
$\mathbb {Z}$
-subshift whose language consists of the left-extendable words in the language of
![]() $Y''$
. Let Y be the subshift of
$Y''$
. Let Y be the subshift of
![]() $Y'$
with additional forbidden words
$Y'$
with additional forbidden words
(where the
![]() $u_i$
are quantified over
$u_i$
are quantified over
![]() $A^*$
). The double occurrences of
$A^*$
). The double occurrences of
![]() $\#$
fit this pattern by picking empty words
$\#$
fit this pattern by picking empty words
![]() $u_i$
.
$u_i$
.
Say that a set of words
![]() $U \subset A^*$
is a friendship if for any finite subset
$U \subset A^*$
is a friendship if for any finite subset
![]() $V \subset U$
there exist points
$V \subset U$
there exist points
![]() $(b_v)_v \in X^V$
such that
$(b_v)_v \in X^V$
such that
![]() $\text { for all } u, v \in V: b_u \in [u] \wedge (b_u, b_v) \in E$
, so since E is doubly shift-invariant, the forbidden words of Y precisely require that the set of words
$\text { for all } u, v \in V: b_u \in [u] \wedge (b_u, b_v) \in E$
, so since E is doubly shift-invariant, the forbidden words of Y precisely require that the set of words
![]() $U \subset A^*$
that appear in y is a friendship. (We remark that even for a closed doubly shift-invariant equivalence relation, for a finite set U, in general, being a friendship is stronger than all pairs
$U \subset A^*$
that appear in y is a friendship. (We remark that even for a closed doubly shift-invariant equivalence relation, for a finite set U, in general, being a friendship is stronger than all pairs
![]() $\{u, v\}$
being friendships for
$\{u, v\}$
being friendships for
![]() $u, v \in U$
.)
$u, v \in U$
.)
For a concrete picture of points in
![]() $Y'$
, consider the sequence
$Y'$
, consider the sequence
![]() $w_\omega \in \{0,1\}^{\mathbb {N}}$
. Its two-sided orbit closure contains points of the form
$w_\omega \in \{0,1\}^{\mathbb {N}}$
. Its two-sided orbit closure contains points of the form
We allow any of the
![]() $1$
s to be duplicated, e.g.
$1$
s to be duplicated, e.g.
and then replace the
![]() $1$
s by
$1$
s by
![]() $\#$
, that is,
$\#$
, that is,
finally replace maximal
![]() $0$
-sequences by words over A of the same length, e.g.
$0$
-sequences by words over A of the same length, e.g.
if
![]() $A = \{0,1\}$
. Such are the points of
$A = \{0,1\}$
. Such are the points of
![]() $Y'$
. In points of Y, the finite words should additionally be from the language of X, and should form a friendship.
$Y'$
. In points of Y, the finite words should additionally be from the language of X, and should form a friendship.
If
![]() $U \subset A^*$
is a friendship, then by compactness to every word
$U \subset A^*$
is a friendship, then by compactness to every word
![]() $u \in U$
, we can associate a point
$u \in U$
, we can associate a point
![]() $b_u \in [u]$
, so that
$b_u \in [u]$
, so that
![]() $(b_u, b_v) \in E$
for all
$(b_u, b_v) \in E$
for all
![]() $u, v \in U$
. Fix such points for each set U and call
$u, v \in U$
. Fix such points for each set U and call
![]() $b_u$
the (friendship) bracelet of u (with respect to U). Of particular importance in what follows are (sets of) bracelets for sets of words
$b_u$
the (friendship) bracelet of u (with respect to U). Of particular importance in what follows are (sets of) bracelets for sets of words
![]() $U \subset A^*$
that appear in some point
$U \subset A^*$
that appear in some point
![]() $y \in Y$
, or the union of such sets for two points
$y \in Y$
, or the union of such sets for two points
![]() $y, z$
. (It is worth noting that in such a situation, the bracelets are not enforced to be in the orbit closure of y or z.)
$y, z$
. (It is worth noting that in such a situation, the bracelets are not enforced to be in the orbit closure of y or z.)
Call the binary word
![]() $\tau '(w)$
recording positions of
$\tau '(w)$
recording positions of
![]() $\#$
by
$\#$
by
![]() $1$
in a word w the skeleton, similarly for points
$1$
in a word w the skeleton, similarly for points
![]() $x \in Y$
, and the word where each maximal occurrence of
$x \in Y$
, and the word where each maximal occurrence of
![]() $11$
is further replaced by
$11$
is further replaced by
![]() $1$
the preskeleton. We call a (positioned or not) word
$1$
the preskeleton. We call a (positioned or not) word
![]() $w \in \hat A^* \cup \hat A^{**}$
full if it is equal to (a shift of)
$w \in \hat A^* \cup \hat A^{**}$
full if it is equal to (a shift of)
![]() $(\tau ')^{-1}(w_n)$
for some n, or if (more generally) its preskeleton is full.
$(\tau ')^{-1}(w_n)$
for some n, or if (more generally) its preskeleton is full.
We now explain the technical trick for characterizing the entropy pairs
![]() $\mathrm {EP}(Y)$
, and show that
$\mathrm {EP}(Y)$
, and show that
![]() $(y,z) \notin \Delta _Y$
is an entropy pair if and only if the set
$(y,z) \notin \Delta _Y$
is an entropy pair if and only if the set
containing all non-
![]() $\#$
subwords from y and z, is a friendship.
$\#$
subwords from y and z, is a friendship.
Suppose
![]() $u', v' \in \hat A^{**}$
are any two positioned words that appear in some points of Y, with
$u', v' \in \hat A^{**}$
are any two positioned words that appear in some points of Y, with
![]() $\#$
as their first and last symbols (note that words beginning and ending with
$\#$
as their first and last symbols (note that words beginning and ending with
![]() $\#$
are dense in Y in the natural topology of
$\#$
are dense in Y in the natural topology of
![]() $\hat A^{**} \cup \hat A^{\mathbb {Z}}$
), and let U be the set of words containing
$\hat A^{**} \cup \hat A^{\mathbb {Z}}$
), and let U be the set of words containing
![]() $u \in A^*$
if and only if
$u \in A^*$
if and only if
![]() $\#u\# \sqsubset u'$
or
$\#u\# \sqsubset u'$
or
![]() $\#u\# \sqsubset v'$
. Suppose U is a friendship. Extend
$\#u\# \sqsubset v'$
. Suppose U is a friendship. Extend
![]() $u'$
and
$u'$
and
![]() $v'$
to full positioned words whose preskeletons are the same length, in an arbitrary way, though so that their finite subwords over
$v'$
to full positioned words whose preskeletons are the same length, in an arbitrary way, though so that their finite subwords over
![]() $A^*$
remain a friendship (safe continuations for words can always be found in the bracelets proving the friendship). The left and right ends of the resulting words
$A^*$
remain a friendship (safe continuations for words can always be found in the bracelets proving the friendship). The left and right ends of the resulting words
![]() $u''$
and
$u''$
and
![]() $v''$
have some left and right offsets
$v''$
have some left and right offsets
![]() $n_1, n_2$
, respectively, in the sense that
$n_1, n_2$
, respectively, in the sense that
![]() $u'' \in A^{[a,b]}$
and
$u'' \in A^{[a,b]}$
and
![]() $v'' \in A^{[a+n_1,b+n_2]}$
.
$v'' \in A^{[a+n_1,b+n_2]}$
.
Now, continue extending the words by alternately turning them into full positioned words by adding a left and a right full extension, so that no new occurrence of
![]() $\#\#$
appears, and all finite subwords over
$\#\#$
appears, and all finite subwords over
![]() $A^*$
remain a friendship. Note that the left and right ends continue to differ by exactly
$A^*$
remain a friendship. Note that the left and right ends continue to differ by exactly
![]() $n_1$
and
$n_1$
and
![]() $n_2$
, since the length of the left or right continuation is always the same if no occurrence of
$n_2$
, since the length of the left or right continuation is always the same if no occurrence of
![]() $\#\#$
appears. Extend the words so many times that at least
$\#\#$
appears. Extend the words so many times that at least
![]() $\max (|n_1|, |n_2|)$
undoubled
$\max (|n_1|, |n_2|)$
undoubled
![]() $\#$
s are obtained on both sides. Now finally double some of the
$\#$
s are obtained on both sides. Now finally double some of the
![]() $\#$
to get two positioned full words
$\#$
to get two positioned full words
![]() $u, v$
which have
$u, v$
which have
![]() $u'$
and
$u'$
and
![]() $v'$
at the center, have the same preskeleton, and have the same left and right length, that is,
$v'$
at the center, have the same preskeleton, and have the same left and right length, that is,
![]() $u, v \in A^{[c,d]}$
for some
$u, v \in A^{[c,d]}$
for some
![]() $c, d \in \mathbb {Z}$
.
$c, d \in \mathbb {Z}$
.
Now suppose u and v have preskeleton
![]() $w_i$
. By the analysis of the density of
$w_i$
. By the analysis of the density of
![]() $1$
s in the ruler sequence, for each k, we can find a word
$1$
s in the ruler sequence, for each k, we can find a word
![]() $w \in (\hat A \cup \{\text {\textvisiblespace }\})^*$
of length at most
$w \in (\hat A \cup \{\text {\textvisiblespace }\})^*$
of length at most
![]() $2k$
such that:
$2k$
such that:
-
• the
 $\text {\textvisiblespace }$
-symbols appear in segments of length exactly
$\text {\textvisiblespace }$
-symbols appear in segments of length exactly
 $|u| = |v|$
;
$|u| = |v|$
; -
• there are at least
 $k/(3 \cdot 2^i) - 2$
such segments; and
$k/(3 \cdot 2^i) - 2$
such segments; and -
• replacing the
 $\text {\textvisiblespace }^{|u|}$
-subwords individually by u or v always leads to a valid word of Y.
$\text {\textvisiblespace }^{|u|}$
-subwords individually by u or v always leads to a valid word of Y.
To see this, recall that for all k, we can find a word of length k in the ruler sequence with at least
![]() $k/3$
many
$k/3$
many
![]() $1$
-symbols. Observing that all
$1$
-symbols. Observing that all
![]() $1$
s appear in disjoint
$1$
s appear in disjoint
![]() $w_i$
-words, we can have at least
$w_i$
-words, we can have at least
![]() $k/(3 \cdot 2^i) - 2$
occurrences of
$k/(3 \cdot 2^i) - 2$
occurrences of
![]() $w_i$
in a word
$w_i$
in a word
![]() $w'$
of length k in the ruler sequence. Replacing these occurrences of
$w'$
of length k in the ruler sequence. Replacing these occurrences of
![]() $w_i$
by
$w_i$
by
![]() $\text {\textvisiblespace }^{|u|}$
in
$\text {\textvisiblespace }^{|u|}$
in
![]() $w'$
, and then filling the remaining gaps with arbitrary words from the bracelets of words in U, we obtain a word w with the desired properties.
$w'$
, and then filling the remaining gaps with arbitrary words from the bracelets of words in U, we obtain a word w with the desired properties.
The interchangeability, together with the lower bound on maximal density, shows that the cover
![]() $([u]^c, [v]^c)$
generates entropy in Y, and thus we have shown that any points whose non-
$([u]^c, [v]^c)$
generates entropy in Y, and thus we have shown that any points whose non-
![]() $\#$
subwords form a friendship are entropy pairs. However, if the union
$\#$
subwords form a friendship are entropy pairs. However, if the union
![]() $U \subset A^*$
of the sets of subwords of two words
$U \subset A^*$
of the sets of subwords of two words
![]() $u, v$
is not a friendship, then these words do not even appear together in any point of Y, by definition, so neither can u and v, and it follows that the cover
$u, v$
is not a friendship, then these words do not even appear together in any point of Y, by definition, so neither can u and v, and it follows that the cover
![]() $([u]^c, [v]^c)$
has zero entropy. This concludes the characterization of
$([u]^c, [v]^c)$
has zero entropy. This concludes the characterization of
![]() $\mathrm {EP}(Y)$
.
$\mathrm {EP}(Y)$
.
An important corollary of this characterization is that
![]() $\mathrm {EP}(Y)$
is doubly shift-invariant, and therefore so is any
$\mathrm {EP}(Y)$
is doubly shift-invariant, and therefore so is any
![]() $\mathrm {EP}(Y)^{(\lambda )}$
by an obvious transfinite induction. If
$\mathrm {EP}(Y)^{(\lambda )}$
by an obvious transfinite induction. If
![]() $(x, y) \in F$
and F is a doubly shift-invariant closed relation, then
$(x, y) \in F$
and F is a doubly shift-invariant closed relation, then
![]() $(x', y) \in F$
for any
$(x', y) \in F$
for any
![]() $x'$
in
$x'$
in
![]() $\overline {\mathcal {O}(x)}$
. Let us call a doubly shift-invariant equivalence relation F with this property hereditary. It is easy to show by transfinite induction that if a doubly shift-invariant equivalence relation F is hereditary, then so is
$\overline {\mathcal {O}(x)}$
. Let us call a doubly shift-invariant equivalence relation F with this property hereditary. It is easy to show by transfinite induction that if a doubly shift-invariant equivalence relation F is hereditary, then so is
![]() $F^{(\lambda )}$
, for any ordinal
$F^{(\lambda )}$
, for any ordinal
![]() $\lambda $
. In particular, the relations
$\lambda $
. In particular, the relations
![]() $\mathrm {EP}(Y)^{(\lambda )}$
are all hereditary since
$\mathrm {EP}(Y)^{(\lambda )}$
are all hereditary since
![]() $\mathrm {EP}(Y)$
is doubly shift-invariant and closed.
$\mathrm {EP}(Y)$
is doubly shift-invariant and closed.
It is clear from the characterization that
![]() $\mathrm {EP}(Y) \cap X^2 = E$
as required. We need to show
$\mathrm {EP}(Y) \cap X^2 = E$
as required. We need to show
![]() $\mathrm {EP}(Y)^{(\lambda )} \cap X^2 = E^{(\lambda )}$
for all
$\mathrm {EP}(Y)^{(\lambda )} \cap X^2 = E^{(\lambda )}$
for all
![]() $\lambda $
, and we do this by transfinite induction. On limit ordinal steps, this obviously continues to hold. On even successor steps, that is, transitive closure steps, we use the fact that points of Y can be replaced by any point in their orbit closure, and the orbit-closure of every point contains a point of X. This allows turning any transitivity sequence
$\lambda $
, and we do this by transfinite induction. On limit ordinal steps, this obviously continues to hold. On even successor steps, that is, transitive closure steps, we use the fact that points of Y can be replaced by any point in their orbit closure, and the orbit-closure of every point contains a point of X. This allows turning any transitivity sequence
![]() $(x = y_0, y_1, \ldots , y_k = x')$
, where
$(x = y_0, y_1, \ldots , y_k = x')$
, where
![]() $x, x' \in X$
,
$x, x' \in X$
,
![]() $y_i \in Y$
,
$y_i \in Y$
,
![]() $(y_i, y_{i+1}) \in E^{(\lambda -1)}$
, into one where
$(y_i, y_{i+1}) \in E^{(\lambda -1)}$
, into one where
![]() $y_i \in X$
for all i. This shows
$y_i \in X$
for all i. This shows
![]() $(\mathrm {EP}(Y)^{(\lambda -1)})^* \cap X^2 = (\mathrm {EP}(Y)^{(\lambda -1)} \cap X^2)^*$
as required.
$(\mathrm {EP}(Y)^{(\lambda -1)})^* \cap X^2 = (\mathrm {EP}(Y)^{(\lambda -1)} \cap X^2)^*$
as required.
Now, note that if
![]() $\mathrm {EP}(Y)^{(\lambda )}$
is transitively closed,
$\mathrm {EP}(Y)^{(\lambda )}$
is transitively closed,
![]() $y \in Y \setminus X$
and b is any bracelet of y, or more generally, any point in X whose set of
$y \in Y \setminus X$
and b is any bracelet of y, or more generally, any point in X whose set of
![]() $A^*$
-subwords together with
$A^*$
-subwords together with
![]() $A^*$
-subwords of Y forms a friendship, then we have
$A^*$
-subwords of Y forms a friendship, then we have
![]() $(y, z) \in \mathrm {EP}(Y)^{(\lambda )}$
if and only if
$(y, z) \in \mathrm {EP}(Y)^{(\lambda )}$
if and only if
![]() $(b, z) \in \mathrm {EP}(Y)^{(\lambda )}$
. This is because
$(b, z) \in \mathrm {EP}(Y)^{(\lambda )}$
. This is because
![]() $(b, y) \in \mathrm {EP}(Y)$
by the characterization of entropy pairs of Y. In other words, on every transitive step, every
$(b, y) \in \mathrm {EP}(Y)$
by the characterization of entropy pairs of Y. In other words, on every transitive step, every
![]() $y \in Y$
satisfies the same relations as any of its bracelets or any point that could be chosen as a bracelet for it.
$y \in Y$
satisfies the same relations as any of its bracelets or any point that could be chosen as a bracelet for it.
On a topological closure step, that is, for an odd ordinal
![]() $\lambda $
, suppose
$\lambda $
, suppose
![]() $\lim _i (x_i, y_i) = (x, y) \in X^2$
where
$\lim _i (x_i, y_i) = (x, y) \in X^2$
where
![]() $(x_i, y_i) \in \mathrm {EP}(Y)^{(\lambda -1)}$
for all i. It is enough to show that the
$(x_i, y_i) \in \mathrm {EP}(Y)^{(\lambda -1)}$
for all i. It is enough to show that the
![]() $x_i$
can be replaced by points from X, as then (also applying this idea to the right component) we have
$x_i$
can be replaced by points from X, as then (also applying this idea to the right component) we have
![]() $\overline {\mathrm {EP}(Y)^{(\lambda -1)}} \cap X^2 = \overline {\mathrm {EP}(Y)^{\lambda -1} \cap X^2}$
. If there is a subsequence of the
$\overline {\mathrm {EP}(Y)^{(\lambda -1)}} \cap X^2 = \overline {\mathrm {EP}(Y)^{\lambda -1} \cap X^2}$
. If there is a subsequence of the
![]() $x_i$
in X, then we can directly restrict to that. Otherwise, restrict to a subsequence such that
$x_i$
in X, then we can directly restrict to that. Otherwise, restrict to a subsequence such that
![]() $x_i \notin X$
for all i.
$x_i \notin X$
for all i.
In
![]() $x_i$
, take a maximal central positioned word
$x_i$
, take a maximal central positioned word
![]() $u_i : A^{[-a, a]}$
not containing
$u_i : A^{[-a, a]}$
not containing
![]() $\#$
(where necessarily
$\#$
(where necessarily
![]() $a \rightarrow \infty $
as
$a \rightarrow \infty $
as
![]() $i \rightarrow \infty $
) and replace
$i \rightarrow \infty $
) and replace
![]() $x_i$
by the bracelet
$x_i$
by the bracelet
![]() $b_{u_i}$
with respect to the language of
$b_{u_i}$
with respect to the language of
![]() $x_i$
, centered to have
$x_i$
, centered to have
![]() $u_i$
in the same place as in
$u_i$
in the same place as in
![]() $x_i$
. We have
$x_i$
. We have
![]() $(b_{u_i}, y_i) \in \mathrm {EP}(Y)^{(\lambda -1)}$
since
$(b_{u_i}, y_i) \in \mathrm {EP}(Y)^{(\lambda -1)}$
since
![]() $\mathrm {EP}(Y)^{(\lambda -1)}$
is transitively closed and
$\mathrm {EP}(Y)^{(\lambda -1)}$
is transitively closed and
![]() $(b_{u_i}, x_i) \in \mathrm {EP}(Y)$
, and clearly
$(b_{u_i}, x_i) \in \mathrm {EP}(Y)$
, and clearly
![]() $(b_{u_i}, y_i) \rightarrow (x,y)$
, as required.
$(b_{u_i}, y_i) \rightarrow (x,y)$
, as required.
Finally, we verify the last claim. Suppose thus that
![]() $E^{(\lambda )} = X^2$
for some
$E^{(\lambda )} = X^2$
for some
![]() $\lambda $
. If
$\lambda $
. If
![]() $\lambda $
is even, then
$\lambda $
is even, then
![]() $\mathrm {EP}(Y)^{(\lambda )}$
is transitively closed so since any
$\mathrm {EP}(Y)^{(\lambda )}$
is transitively closed so since any
![]() $y \in Y \setminus X$
appears in the same relations as any bracelet of its,
$y \in Y \setminus X$
appears in the same relations as any bracelet of its,
![]() $\mathrm {EP}(Y)^{(\lambda )} = Y^2$
.
$\mathrm {EP}(Y)^{(\lambda )} = Y^2$
.
Suppose then that
![]() $\lambda $
is odd. Let
$\lambda $
is odd. Let
![]() $(y, z) \in Y^2$
, and without loss of generality suppose
$(y, z) \in Y^2$
, and without loss of generality suppose
![]() $y, z \in Y \setminus X$
(this suffices since
$y, z \in Y \setminus X$
(this suffices since
![]() $\mathrm {EP}(Y)^{(\lambda )}$
is closed and
$\mathrm {EP}(Y)^{(\lambda )}$
is closed and
![]() $X \subset \overline {Y \setminus X}$
). Let
$X \subset \overline {Y \setminus X}$
). Let
![]() $(b_u)_u$
and
$(b_u)_u$
and
![]() $(c_v)_v$
be the respective bracelets of their subwords with respect to their languages. If any two of these bracelets, one from y and one from z, are in relation on step
$(c_v)_v$
be the respective bracelets of their subwords with respect to their languages. If any two of these bracelets, one from y and one from z, are in relation on step
![]() $\lambda -1$
, then already
$\lambda -1$
, then already
![]() $(y, z) \in \mathrm {EP}(Y)^{(\lambda -1)}$
since
$(y, z) \in \mathrm {EP}(Y)^{(\lambda -1)}$
since
![]() $\mathrm {EP}(Y)^{(\lambda -1)}$
is transitive.
$\mathrm {EP}(Y)^{(\lambda -1)}$
is transitive.
Otherwise, let m be arbitrary and let (up to swapping y and z)
![]() $n \geq m$
and k be such that
$n \geq m$
and k be such that
![]() $y_{[-m,m]} = u_1\#u_2\#\ldots \#u_k$
,
$y_{[-m,m]} = u_1\#u_2\#\ldots \#u_k$
,
![]() $U = (u_1, \ldots , u_k) \in (A^*)^k$
and
$U = (u_1, \ldots , u_k) \in (A^*)^k$
and
![]() $z_{[-m,n]} = v_1\#v_2\#\ldots \#v_k$
,
$z_{[-m,n]} = v_1\#v_2\#\ldots \#v_k$
,
![]() $V = (v_1, \ldots , v_k) \in (A^*)^k$
. Let
$V = (v_1, \ldots , v_k) \in (A^*)^k$
. Let
![]() $B = (b_u)_{u \in U}$
and
$B = (b_u)_{u \in U}$
and
![]() $C = (c_v)_{v \in V}$
be bracelets for these words with respect to the subwords of y and z, respectively.
$C = (c_v)_{v \in V}$
be bracelets for these words with respect to the subwords of y and z, respectively.
Now, recall that the bracelets of a point are always (by definition) in the E-relation together, and apply the odd condition to
![]() $(B, C) \in (E^{(k)})^2$
. Since
$(B, C) \in (E^{(k)})^2$
. Since
![]() $(E^{[k]})^2 \subset \overline {(E^{(\lambda -1)})^{[2k]} \cap (E^{[k]})^2}$
, we can find in
$(E^{[k]})^2 \subset \overline {(E^{(\lambda -1)})^{[2k]} \cap (E^{[k]})^2}$
, we can find in
![]() $(E^{(\lambda -1)})^{[2k]} \cap (E^{[k]})^2$
arbitrarily good approximations
$(E^{(\lambda -1)})^{[2k]} \cap (E^{[k]})^2$
arbitrarily good approximations
![]() $B' = (b_u')_{u \in U}$
and
$B' = (b_u')_{u \in U}$
and
![]() $C' = (c_v')_{v \in V}$
to B and C, respectively. In particular, we can find good enough approximations to ensure that
$C' = (c_v')_{v \in V}$
to B and C, respectively. In particular, we can find good enough approximations to ensure that
![]() $b_u'$
contains u and
$b_u'$
contains u and
![]() $c^{\prime }_v$
contains v, for each
$c^{\prime }_v$
contains v, for each
![]() $u \in U, v \in V$
. Then since
$u \in U, v \in V$
. Then since
![]() $\mathrm {EP}(Y)^{(\lambda -1)}$
is transitive and
$\mathrm {EP}(Y)^{(\lambda -1)}$
is transitive and
![]() $(b_u', c^{\prime }_v) \in E^{(\lambda -1)}$
, any pair of points
$(b_u', c^{\prime }_v) \in E^{(\lambda -1)}$
, any pair of points
![]() $(y_k, z_k)$
in Y, for which we can take
$(y_k, z_k)$
in Y, for which we can take
![]() $b_u'$
and
$b_u'$
and
![]() $c^{\prime }_v$
as one of their bracelets, satisfies
$c^{\prime }_v$
as one of their bracelets, satisfies
![]() $(y_k, z_k) \in \mathrm {EP}(Y)^{(\lambda -1)}$
.
$(y_k, z_k) \in \mathrm {EP}(Y)^{(\lambda -1)}$
.
We construct the pair
![]() $y_k, z_k$
so that
$y_k, z_k$
so that
![]() $(y_k, z_k)_{[-k,k]} = (y,z)_{[-k,k]}$
. For this, directly let
$(y_k, z_k)_{[-k,k]} = (y,z)_{[-k,k]}$
. For this, directly let
![]() $(y_k)_{[-m,m]} = u_1\#u_2\#\ldots \#u_k$
and
$(y_k)_{[-m,m]} = u_1\#u_2\#\ldots \#u_k$
and
![]() $(z_k)_{[-m,n]} = v_1\#v_2\#\ldots \#v_k$
. Extend
$(z_k)_{[-m,n]} = v_1\#v_2\#\ldots \#v_k$
. Extend
![]() $y_k$
to a point of Y by copying the skeleton from y and filling all the remaining gaps arbitrarily so that all words between two
$y_k$
to a point of Y by copying the skeleton from y and filling all the remaining gaps arbitrarily so that all words between two
![]() $\#$
s (and possible infinite tails without an occurrence of
$\#$
s (and possible infinite tails without an occurrence of
![]() $\#$
) are subwords of the words in
$\#$
) are subwords of the words in
![]() $B'$
. Extend
$B'$
. Extend
![]() $z_k$
similarly. These are indeed valid points: the skeletons are correct since we copied them from valid points, and the set of
$z_k$
similarly. These are indeed valid points: the skeletons are correct since we copied them from valid points, and the set of
![]() $A^*$
-subwords of each point is a friendship, since
$A^*$
-subwords of each point is a friendship, since
![]() $B', C' \in E^{[k]}$
. Clearly we can take any
$B', C' \in E^{[k]}$
. Clearly we can take any
![]() $b_u'$
and
$b_u'$
and
![]() $c^{\prime }_v$
as one of their bracelets, so
$c^{\prime }_v$
as one of their bracelets, so
![]() $(y_k, z_k) \in \mathrm {EP}(Y)^{(\lambda -1)}$
gives an approximation to
$(y_k, z_k) \in \mathrm {EP}(Y)^{(\lambda -1)}$
gives an approximation to
![]() $(y,z)$
that is correct in the interval
$(y,z)$
that is correct in the interval
![]() $[-m,m]$
.
$[-m,m]$
.
3.5 Implementation of arbitrary CPE ranks
For the main proof, we make some simple topological observations.
Lemma 9. Suppose
![]() $X, Y$
are first-countable topological spaces, and
$X, Y$
are first-countable topological spaces, and
![]() $f : X \to Y$
is a quotient map. Then the following are equivalent:
$f : X \to Y$
is a quotient map. Then the following are equivalent:
-
• f is open;
-
• whenever
 $\lim _i y_i = y \in Y$
and
$\lim _i y_i = y \in Y$
and
 $f(x) = y$
, then there exist
$f(x) = y$
, then there exist
 $x_i \in X$
such that
$x_i \in X$
such that
 $f(x_i) = y_i$
and
$f(x_i) = y_i$
and
 $\lim _i x_i = x$
.
$\lim _i x_i = x$
.
Proof. Suppose f is open and
![]() $f(x) = y$
. Then every neighborhood
$f(x) = y$
. Then every neighborhood
![]() $U \ni x$
maps to a neighborhood
$U \ni x$
maps to a neighborhood
![]() $f(U)$
of y, in particular, if
$f(U)$
of y, in particular, if
![]() $\lim _i y_i = y$
, then for all large enough i,
$\lim _i y_i = y$
, then for all large enough i,
![]() $y_i$
has a preimage
$y_i$
has a preimage
![]() $x_i$
in U. Picking open sets U from a decreasing countable neighborhood basis of x, and always picking preimages for
$x_i$
in U. Picking open sets U from a decreasing countable neighborhood basis of x, and always picking preimages for
![]() $y_i$
from U until they start having preimages in the next neighborhood of x, the claim is proved.
$y_i$
from U until they start having preimages in the next neighborhood of x, the claim is proved.
For the other direction, suppose f is not open, and let U be open such that for some
![]() $y \in f(U)$
, every neighborhood of y contains a point without a preimage in U. Pick
$y \in f(U)$
, every neighborhood of y contains a point without a preimage in U. Pick
![]() $x \in U$
such that
$x \in U$
such that
![]() $f(x) = y$
. By first-countability, there is a sequence
$f(x) = y$
. By first-countability, there is a sequence
![]() $y_i \rightarrow y$
such that the points
$y_i \rightarrow y$
such that the points
![]() $y_i$
have no preimage in U. The second condition fails, since we cannot pick
$y_i$
have no preimage in U. The second condition fails, since we cannot pick
![]() $x_i \in U$
.
$x_i \in U$
.
The following lemmas explain why we want
![]() $\phi $
to be open.
$\phi $
to be open.
Lemma 10. Let
![]() $X,Y$
be first-countable topological spaces. Let
$X,Y$
be first-countable topological spaces. Let
![]() $f : X \to Y$
be an open quotient map,
$f : X \to Y$
be an open quotient map,
![]() $E \subset Y^2$
a symmetric reflexive closed relation, and
$E \subset Y^2$
a symmetric reflexive closed relation, and
![]() $F = (f^{-1} \times f^{-1})(E)$
. Then
$F = (f^{-1} \times f^{-1})(E)$
. Then
![]() $F^{(\lambda )} = (f^{-1} \times f^{-1})(E^{(\lambda )})$
for all ordinals
$F^{(\lambda )} = (f^{-1} \times f^{-1})(E^{(\lambda )})$
for all ordinals
![]() $\lambda $
.
$\lambda $
.
Proof. Since X is first-countable, so is
![]() $X^2$
, and thus the closure of a set
$X^2$
, and thus the closure of a set
![]() $C \subset X^2$
is just the set of limits of sequences in C. (In other words,
$C \subset X^2$
is just the set of limits of sequences in C. (In other words,
![]() $X^2$
has the Fréchet–Urysohn property. For general topological spaces, even if X is Frechét–Urysohn,
$X^2$
has the Fréchet–Urysohn property. For general topological spaces, even if X is Frechét–Urysohn,
![]() $X^2$
need not be [Reference Gruenhage8].)
$X^2$
need not be [Reference Gruenhage8].)
Write
![]() $g = f \times f : X^2 \to Y^2$
, and observe this is also an open quotient map. We have
$g = f \times f : X^2 \to Y^2$
, and observe this is also an open quotient map. We have
![]() $F^{(\zeta )} = g^{-1}(E^{(\zeta )})$
where
$F^{(\zeta )} = g^{-1}(E^{(\zeta )})$
where
![]() $\zeta = 0$
if E is not closed, and
$\zeta = 0$
if E is not closed, and
![]() $\zeta = 1$
otherwise, since E is closed if and only if F is closed since g is a quotient map. We proceed by induction. Suppose
$\zeta = 1$
otherwise, since E is closed if and only if F is closed since g is a quotient map. We proceed by induction. Suppose
![]() $\lambda $
is an odd ordinal, and
$\lambda $
is an odd ordinal, and
![]() $g(x,x') = (y,y')$
. If
$g(x,x') = (y,y')$
. If
![]() $(x,x') \in F^{(\lambda )}$
, then there exist
$(x,x') \in F^{(\lambda )}$
, then there exist
![]() $(x_i,x_i') \in F^{(\lambda -1)}$
with
$(x_i,x_i') \in F^{(\lambda -1)}$
with
![]() $(x_i,x_i') \rightarrow (x,x')$
and then
$(x_i,x_i') \rightarrow (x,x')$
and then
![]() $g(x_i,x_i') \rightarrow (y,y')$
by continuity showing
$g(x_i,x_i') \rightarrow (y,y')$
by continuity showing
![]() $E^{(\lambda )} \supset g(F^{(\lambda )})$
, which implies
$E^{(\lambda )} \supset g(F^{(\lambda )})$
, which implies
![]() $g^{-1}(E^{(\lambda )}) \supset F^{(\lambda )}$
.
$g^{-1}(E^{(\lambda )}) \supset F^{(\lambda )}$
.
For the other inclusion, suppose
![]() $(y, y') \in E^{(\lambda )}$
, so
$(y, y') \in E^{(\lambda )}$
, so
![]() $(y, y') = \lim _i (y_i, y_i')$
for some
$(y, y') = \lim _i (y_i, y_i')$
for some
![]() $(y_i, y_i') \in E^{(\lambda -1)}$
. By the previous lemma, there exist
$(y_i, y_i') \in E^{(\lambda -1)}$
. By the previous lemma, there exist
![]() $(x_i,x_i') \in X^2$
such that
$(x_i,x_i') \in X^2$
such that
![]() $g(x_i,x_i') = (y,y')$
and
$g(x_i,x_i') = (y,y')$
and
![]() $(x_i, x_i') \rightarrow (x, x')$
. Then by induction, we have
$(x_i, x_i') \rightarrow (x, x')$
. Then by induction, we have
![]() $(x_i,x_i') \in F^{(\lambda -1)}$
for all i, so
$(x_i,x_i') \in F^{(\lambda -1)}$
for all i, so
![]() $(x,x') \in F^{(\lambda )}$
, showing
$(x,x') \in F^{(\lambda )}$
, showing
![]() $g^{-1}(E^{(\lambda )}) \subset F^{(\lambda )}$
.
$g^{-1}(E^{(\lambda )}) \subset F^{(\lambda )}$
.
If
![]() $\lambda $
is an even successor ordinal, suppose
$\lambda $
is an even successor ordinal, suppose
![]() $g(x,x') = (y,y')$
. If
$g(x,x') = (y,y')$
. If
![]() $(x,x') \in F^{(\lambda )}$
, there exist
$(x,x') \in F^{(\lambda )}$
, there exist
![]() $x = x_0, x_1, \ldots , x_k = x'$
such that
$x = x_0, x_1, \ldots , x_k = x'$
such that
![]() $(x_i, x_{i+1}) \in F^{(\lambda -1)}$
for all i, and then by induction,
$(x_i, x_{i+1}) \in F^{(\lambda -1)}$
for all i, and then by induction,
![]() $g(x_i, x_{i+1}) \in E^{(\lambda -1)}$
and since
$g(x_i, x_{i+1}) \in E^{(\lambda -1)}$
and since
![]() $y = f(x_0), y' = f(x_k)$
, we have
$y = f(x_0), y' = f(x_k)$
, we have
![]() $(y,y') \in E^{(\lambda )}$
.
$(y,y') \in E^{(\lambda )}$
.
If however
![]() $(y, y') \in E^{(\lambda )}$
, then there exist
$(y, y') \in E^{(\lambda )}$
, then there exist
![]() $y = y_0, y_1,\ldots , y_k = y'$
with
$y = y_0, y_1,\ldots , y_k = y'$
with
![]() $(y_i, y_{i+1}) \in E^{(\lambda -1)}$
. Pick any preimages
$(y_i, y_{i+1}) \in E^{(\lambda -1)}$
. Pick any preimages
![]() $f(x_i) = y_i$
with
$f(x_i) = y_i$
with
![]() $x_0 = x, x_k = x'$
by induction
$x_0 = x, x_k = x'$
by induction
![]() $(x_i, x_{i+1}) \in F^{(\lambda -1)}$
for all i, and thus
$(x_i, x_{i+1}) \in F^{(\lambda -1)}$
for all i, and thus
![]() $(x,x') \in F^{(\lambda )}$
.
$(x,x') \in F^{(\lambda )}$
.
For the limit ordinal case, observe that union commutes with preimage.
Lemma 11. Let
![]() $X, Y$
be first-countable. Let
$X, Y$
be first-countable. Let
![]() $f : X \to Y$
be an open quotient map,
$f : X \to Y$
be an open quotient map,
![]() $E \subset Y^2$
a symmetric reflexive relation, and
$E \subset Y^2$
a symmetric reflexive relation, and
![]() $F = (f^{-1} \times f^{-1})(E)$
. Then
$F = (f^{-1} \times f^{-1})(E)$
. Then
if and only if
Proof. Suppose
![]() $(E^{[k]})^2 \subset \overline {(E^{(\lambda -1)})^{[2k]} \cap (E^{[k]})^2}$
and consider
$(E^{[k]})^2 \subset \overline {(E^{(\lambda -1)})^{[2k]} \cap (E^{[k]})^2}$
and consider
![]() $(A', B') \in (F^{[k]})^2$
. Consider
$(A', B') \in (F^{[k]})^2$
. Consider
![]() $f(A')$
and
$f(A')$
and
![]() $f(B')$
(where f is applied diagonally to all elements of the tuple), which are by definition k-tuples
$f(B')$
(where f is applied diagonally to all elements of the tuple), which are by definition k-tuples
![]() $A, B \in E^{[k]}$
. In
$A, B \in E^{[k]}$
. In
![]() $(E^{(\lambda -1)})^{[2k]} \cap (E^{[k]})^2$
, we find arbitrarily good approximations
$(E^{(\lambda -1)})^{[2k]} \cap (E^{[k]})^2$
, we find arbitrarily good approximations
![]() $(A_i, B_i)$
to
$(A_i, B_i)$
to
![]() $(A,B)$
. Take any f-preimages,
$(A,B)$
. Take any f-preimages,
![]() $f(A_i') = A_i$
,
$f(A_i') = A_i$
,
![]() $f(B_i') = B_i$
which are close to
$f(B_i') = B_i$
which are close to
![]() $A', B'$
elementwise, using Lemma 9, obtaining by definition
$A', B'$
elementwise, using Lemma 9, obtaining by definition
![]() $A^{\prime }_i, B_i' \in F^{[k]}$
. By the previous lemma, we have
$A^{\prime }_i, B_i' \in F^{[k]}$
. By the previous lemma, we have
![]() $(F^{(\lambda -1)})^{[2k]} = (f \times f)^{-1}(E^{(\lambda -1)})^{[2k]}$
so we have
$(F^{(\lambda -1)})^{[2k]} = (f \times f)^{-1}(E^{(\lambda -1)})^{[2k]}$
so we have
![]() $(A_i', B_i') \in (F^{(\lambda -1)})^{[2k]}$
. This implies
$(A_i', B_i') \in (F^{(\lambda -1)})^{[2k]}$
. This implies
![]() $(F^{[k]})^2 \subset \overline {(F^{(\lambda -1)})^{[2k]} \cap (F^{[k]})^2}$
.
$(F^{[k]})^2 \subset \overline {(F^{(\lambda -1)})^{[2k]} \cap (F^{[k]})^2}$
.
The other direction is similar, but using continuity instead of openness.
Theorem 3. Let
![]() $\alpha \geq 1$
be a countable ordinal. Then there exists a subshift
$\alpha \geq 1$
be a countable ordinal. Then there exists a subshift
![]() $X \subset A^{\mathbb {Z}}$
in CPE class
$X \subset A^{\mathbb {Z}}$
in CPE class
![]() $\alpha $
.
$\alpha $
.
Proof. If
![]() $\alpha = 1$
,
$\alpha = 1$
,
![]() $X = A^{\mathbb {Z}}$
is an example.
$X = A^{\mathbb {Z}}$
is an example.
Let
![]() $\lambda \geq 2$
be a countable ordinal. By Lemma 7, there exists a closed countable set
$\lambda \geq 2$
be a countable ordinal. By Lemma 7, there exists a closed countable set
![]() $Z \subset [0,1]$
and a closed symmetric reflexive relation
$Z \subset [0,1]$
and a closed symmetric reflexive relation
![]() $E \subset Z^2$
such that E is equalizing with close-up rank
$E \subset Z^2$
such that E is equalizing with close-up rank
![]() $\lambda $
. Furthermore, if
$\lambda $
. Furthermore, if
![]() $\lambda $
is an odd ordinal, then
$\lambda $
is an odd ordinal, then
![]() $(E^{[k]})^2 \subset \overline {(E^{(\lambda -1)})^{[2k]} \cap (E^{[k]})^2}$
.
$(E^{[k]})^2 \subset \overline {(E^{(\lambda -1)})^{[2k]} \cap (E^{[k]})^2}$
.
By Lemma 4, since every countable compact subspace of
![]() $[0,1]$
is zero-dimensional, there exists a pointwise zero-entropy Toeplitz subshift X and a doubly shift-invariant closed equivalence relation
$[0,1]$
is zero-dimensional, there exists a pointwise zero-entropy Toeplitz subshift X and a doubly shift-invariant closed equivalence relation
![]() $F \subset X^2$
such that Z is the open quotient of X, by
$F \subset X^2$
such that Z is the open quotient of X, by
![]() $\phi : X \to Z$
, and
$\phi : X \to Z$
, and
![]() $(\phi (x), \phi (y)) \in E\! \iff (x,y) \in F$
.
$(\phi (x), \phi (y)) \in E\! \iff (x,y) \in F$
.
Since
![]() $\phi $
is an open quotient map, Lemma 10 shows that
$\phi $
is an open quotient map, Lemma 10 shows that
![]() $E^{(\lambda )} = Z^2$
if and only if
$E^{(\lambda )} = Z^2$
if and only if
![]() $(\phi ^{-1} \times \phi ^{-1})(E) = F$
satisfies
$(\phi ^{-1} \times \phi ^{-1})(E) = F$
satisfies
![]() $F^{(\lambda )} = X^2$
. If
$F^{(\lambda )} = X^2$
. If
![]() $\lambda $
is an odd ordinal, then
$\lambda $
is an odd ordinal, then
![]() $(E^{[k]})^2 \subset \overline {(E^{(\lambda -1)})^{[2k]} \cap (E^{[k]})^2}$
, and by the previous lemma, we have
$(E^{[k]})^2 \subset \overline {(E^{(\lambda -1)})^{[2k]} \cap (E^{[k]})^2}$
, and by the previous lemma, we have
![]() $(F^{[k]})^2 \subset \overline {(F^{(\lambda -1)})^{[2k]} \cap (F^{[k]})^2}$
.
$(F^{[k]})^2 \subset \overline {(F^{(\lambda -1)})^{[2k]} \cap (F^{[k]})^2}$
.
Now, apply Lemma 5 to obtain
![]() $Y \supset X$
such that
$Y \supset X$
such that
![]() $\lambda $
is the minimal ordinal satisfying
$\lambda $
is the minimal ordinal satisfying
![]() $\mathrm {EP}(Y)^{(\lambda )} = Y^2$
. This Y is a subshift in CPE class
$\mathrm {EP}(Y)^{(\lambda )} = Y^2$
. This Y is a subshift in CPE class
![]() $\lambda $
.
$\lambda $
.
3.6 Not every relation satisfies odd condition
We show that not every relation satisfies the odd condition, at least for one-step processes.
Example 1. Let
![]() $X = [0,3]$
. For
$X = [0,3]$
. For
![]() $i,j \in \{0,1,2\}$
, let
$i,j \in \{0,1,2\}$
, let
![]() $X_{i,j} \subset [i, j+1]$
be a dense set such that
$X_{i,j} \subset [i, j+1]$
be a dense set such that
![]() $X_{i,j} \cap X_{i',j'} = \emptyset $
for
$X_{i,j} \cap X_{i',j'} = \emptyset $
for
![]() $(i,j) \neq (i',j')$
.
$(i,j) \neq (i',j')$
.
Indexing modulo
![]() $3$
, let
$3$
, let
![]() $R_i = X_{i,i+1}^2$
. Now clearly
$R_i = X_{i,i+1}^2$
. Now clearly
![]() $E = R_0 \cup R_1 \cup R_2 \cup \Delta _X$
is reflexive, symmetric, and transitive but is not closed. The close-up rank is
$E = R_0 \cup R_1 \cup R_2 \cup \Delta _X$
is reflexive, symmetric, and transitive but is not closed. The close-up rank is
![]() $1$
:
$1$
:
![]() $E^{(0)} = E$
and
$E^{(0)} = E$
and
![]() $E^{(1)} = [0,3]^2$
.
$E^{(1)} = [0,3]^2$
.
The odd condition
![]() $(E^{[2]})^2 \subset \overline {E^{[4]} \cap (E^{[2]})^2}$
fails because
$(E^{[2]})^2 \subset \overline {E^{[4]} \cap (E^{[2]})^2}$
fails because
![]() $(E^{[2]})^2$
contains quadruples
$(E^{[2]})^2$
contains quadruples
![]() $(x, y, z, w) \in [0,1] \times [1,2] \times [1,2] \times [2,3]$
, while
$(x, y, z, w) \in [0,1] \times [1,2] \times [1,2] \times [2,3]$
, while
![]() $E^{[4]}$
only contains quadruples contained in
$E^{[4]}$
only contains quadruples contained in
![]() $[0,2]^4 \cup [1,3]^4 \cup ([0,1] \cup [2,3])^2$
.
$[0,2]^4 \cup [1,3]^4 \cup ([0,1] \cup [2,3])^2$
.
Acknowledgement
This research was supported by the Academy of Finland grant 2608073211.