Hostname: page-component-745bb68f8f-g4j75 Total loading time: 0 Render date: 2025-01-11T09:32:33.508Z Has data issue: false hasContentIssue false
  • English
  • Français

Entropy of 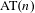$\text{AT}(n)$ systems

Published online by Cambridge University Press:  19 September 2016

RADU B. MUNTEANU
RADU B. MUNTEANU*
Affiliation:
Department of Mathematics, University of Bucharest, 14 Academiei St., 010014 Bucharest, Romania email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we show that any ergodic measure preserving transformation of a standard probability space which is 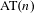$\text{AT}(n)$ for some positive integer $n$ has zero entropy. We show that for every positive integer $n$ any Bernoulli shift is not 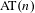$\text{AT}(n)$. We also give an example of a transformation which has zero entropy but does not have property 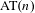$\text{AT}(n)$ for any integer 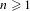$n\geq 1$.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 38 , Issue 3 , May 2018 , pp. 1118 - 1126
Copyright
© Cambridge University Press, 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Connes, A. and Woods, E. J.. Approximately transitive flows and ITPFI factors. Ergod. Th. & Dynam. Sys. 5 (1985), 203–236.Google Scholar
David, M. C.. Sur quelques problèmes de théorie ergodique non commutative. PhD Thesis, Paris VI, 1979.Google Scholar
Dooley, A. H. and Quas, A.. Approximate transitivity for zero-entropy systems. Ergod. Th. & Dynam. Sys. 25 (2005), 443–453.Google Scholar
El Abdalaoui, E. H. and Lemanczyk, M.. Approximate transitivity property and Lebesgue spectrum. Monatsh. Math. 161 (2010), 121–144.Google Scholar
Ferenczi, S.. Systems of finite rank. Colloq. Math. 73 (1997), 35–65.CrossRefGoogle Scholar
Furstenberg, H.. Strict ergodicity and transformations of the torus. Amer. J. Math. 83 (1961), 573–601.Google Scholar
Furstenberg, H.. Recurrence in Ergodic Theory and Combinatorial Number Theory. Princeton University Press, Princeton, NJ, 1981.Google Scholar
Giordano, T. and Handelman, D.. Matrix-valued random walks and variations on property AT. Münster J. Math. 1 (2008), 15–72.Google Scholar
Kolmogorov, A. N.. A new invariant for transitive dynamical systems. Dokl. Akad. Nauk SSSR 119 (1958), 861–869.Google Scholar
Ornstein, D. S.. Bernoulli shifts with the same entropy are isomorphic. Adv. Math. 4 (1970), 337–352.Google Scholar
Sinai, Y. G.. On the concept of entropy for a dynamic system. Dokl. Akad. Nauk SSSR 124 (1959), 768–771.Google Scholar