Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-26T01:14:36.989Z Has data issue: false hasContentIssue false
  • English
  • Français

Entropy of dynamical systems and perturbations of operators

Published online by Cambridge University Press:  19 September 2008

Dan Voiculescu
Dan Voiculescu
Affiliation:
Department of Mathematics, University of California, Berkeley CA 94720, USA
Get access Rights & Permissions [Opens in a new window]

Extract

In the papers [9, 10, 3, 11] on perturbations of Hilbert space operators, we studied an invariant 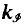(τ) where 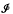is a normed ideal of compact operators and τ a family of operators. The size of an ideal 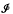for which 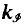(τ) vanishes or does not vanish is an upper, respectively lower, bound for a kind of dimension of τ. In the case of systems of commuting self-adjoint operators τ, the results of [9,3] relate 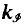(τ) with (an ideal slightly smaller than the Schatten von Neumann class 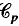) to the way the spectral measure of τ compares to p-dimensional Hausdorff measure.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 11 , Issue 4 , December 1991 , pp. 779 - 786
Copyright
Copyright © Cambridge University Press 1991

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Connes, A. & Størmer, E.. Entropy for automorphisms of II1 von Neumann algebras. Acta Math. 134 (1975), 289–306.Google Scholar
[2]Connes, A., Narnhofer, H. & Thirring, W.. Dynamical entropy of C*-algebras and von Neumann algebras. Commun. Math. Phys. 112 (1987), 691–719.CrossRefGoogle Scholar
[3]David, G. & Voiculescu, D.. s-numbers of singular integrals for invariance of absolutely continuous spectra in fractional dimension. J. Funct. Anal. 94 no. 1 (1990), 14–26.CrossRefGoogle Scholar
[4]Gohberg, I. C. & Krein, M. G.. Introduction to the Theory of Non-selfadjoint Operators. Moscow, 1965.Google Scholar
[5]Kolmogorov, A. N.. A new metric invariant of transient dynamical systems and automorphism of Lebesque spaces. Dokl. Akad. Nauk. SSSR 119 (1958), 861–864.Google Scholar
[6]Parry, W.. Entropy and Generators in Ergodic Theory. Benjamin 1969.Google Scholar
[7]Sinaï, Ja. G.. On the concept of entropy for dynamical systems. Dokl. Akad. Nauk SSSR 124 (1959), 768–771.Google Scholar
[8]Sinaï, Ja. G.. Weak isomorphism of transformations with invariant measure. Mat. Sbornik 63 (105) (1964) 23–42.Google Scholar
[9]Voiculescu, D.. Some results on norm ideal perturbations of Hilbert space operators. I. J. Operator Theory 1 (1979), 3–37;Google Scholar
Some results on norm ideal perturbations of Hilbert space operators. II J. Operator Theory 5 (1981), 77–100.Google Scholar
[10]Voiculescu, D.. On the existence of quasicentral approximate units relative to normed ideals, Part I. J. Funct. Anal. 91 (1990), 1–36.CrossRefGoogle Scholar
[11]Voiculescu, D.. Hilbert space operators modulo normed ideals, Proc. Int. Congress of Mathematicians 1983, Warsaw, pp. 1041–1047.Google Scholar