Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-16T16:14:01.309Z Has data issue: false hasContentIssue false
  • English
  • Français

Entropy, minimal surfaces and negatively curved manifolds

Published online by Cambridge University Press:  04 July 2016

ANDREW SANDERS
ANDREW SANDERS*
Affiliation:
Department of Mathematics, Statistics and Computer Science, University of Illinois at Chicago, Chicago, IL 60607, USA email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Taubes [Minimal surfaces in germs of hyperbolic 3-manifolds. Proceedings of the Casson Fest, Geom. Topol. Monogr.7 (2004), 69–100 (electronic)] introduced the space of minimal hyperbolic germs with elements consisting of the first and second fundamental form of an equivariant immersed minimal disk in hyperbolic 3-space. Herein, we initiate a further study of this space by studying the behavior of a dynamically defined function which records the entropy of the geodesic flow on the associated Riemannian surface. We provide a useful estimate on this function which, in particular, yields a new proof of Bowen’s theorem on the rigidity of the Hausdorff dimension of the limit set of quasi-Fuchsian groups. These follow from new lower bounds on the Hausdorff dimension of the limit set which allow us to give a quantitative version of Bowen’s rigidity theorem. 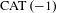To demonstrate the strength of the techniques, these results are generalized to convex-cocompact surface groups acting on $n$-dimensional $\text{CAT}\,(-1)$ Riemannian manifolds.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 38 , Issue 1 , February 2018 , pp. 336 - 370
Copyright
© Cambridge University Press, 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bers, L.. Simultaneous uniformization. Bull. Amer. Math. Soc 66 (1960), 94–97.Google Scholar
Bonk, M. and Kleiner, B.. Rigidity for quasi-Fuchsian actions on negatively curved spaces. Int. Math. Res. Not. 2004(61) (2004), 3309–3316.CrossRefGoogle Scholar
Bourdon, M.. Structure conforme au bord et flot géodésique d’un CAT(-1)-espace. Enseign. Math. (2) 41(1–2) (1995), 63–102.Google Scholar
Bowen, R.. Hausdorff dimension of quasi-circles. Publ. Math. Inst. Hautes Études Sci. 50(1) (1979), 11–25.Google Scholar
Bridgeman, M.. Hausdorff dimension and the Weil–Petersson extension to quasifuchsian space. Geom. Topol. 14(2) (2010), 799–831.Google Scholar
Beeson, M. J. and Tromba, A. J.. The cusp catastrophe of Thom in the bifurcation of minimal surfaces. Manuscripta Math. 46(1–3) (1984), 273–308.Google Scholar
Bridgeman, M. J. and Taylor, E. C.. An extension of the Weil–Petersson metric to quasi-Fuchsian space. Math. Ann. 341(4) (2008), 927–943.Google Scholar
Baird, P. and Wood, J. C.. Harmonic Morphisms Between Riemannian Manifolds (London Mathematical Society Monographs, New Series, 29) . Clarendon, Oxford University Press, Oxford, 2003.Google Scholar
Colding, T. H. and Minicozzi, II, W. P.. A Course in Minimal Surfaces (Graduate Studies in Mathematics, 121) . American Mathematical Society, Providence, RI, 2011.Google Scholar
Coornaert, M.. Mesures de Patterson–Sullivan sur le bord d’un espace hyperbolique au sens de Gromov. Pacific J. Math. 159(2) (1993), 241–270.Google Scholar
Freedman, M., Hass, J. and Scott, P.. Least area incompressible surfaces in 3-manifolds. Invent. Math. 71(3) (1983), 609–642.Google Scholar
Fock, V. V.. Cosh-Gordon equation and quasi-Fuchsian groups. Moscow Seminar on Mathematical Physics. II (American Mathematical Society Translations, Series 2, 221) . American Mathematical Society, Providence, RI, 2007, pp. 49–58.Google Scholar
Guo, R., Huang, Z. and Wang, B.. Quasi-Fuchsian three-manifolds and metrics on Teichmuller space. Asian J. Math. 14(2) (2010), 243–256.Google Scholar
Goldman, W. M.. The complex-symplectic geometry of SL(2, ℂ)-characters over surfaces. Algebraic Groups and Arithmetic. Tata Institute of Fundamental Research, Mumbai, 2004, pp. 375–407.Google Scholar
Gulliver II, R. D., Osserman, R. and Royden, H. L.. A theory of branched immersions of surfaces. Amer. J. Math. 95 (1973), 750–812.Google Scholar
Gray, A.. Tubes (Progress in Mathematics, 221) , 2nd edn. Birkhäuser, Basel, 2004; with a preface by Vicente Miquel.Google Scholar
Gulliver, R. and Tomi, F.. On false branch points of incompressible branched immersions. Manuscripta Math. 63(3) (1989), 293–302.Google Scholar
Gulliver, R.. Branched immersions of surfaces and reduction of topological type. II. Math. Ann. 230(1) (1977), 25–48.Google Scholar
Goldman, W. M. and Wentworth, R. A.. Energy of twisted harmonic maps of Riemann surfaces. In the Tradition of Ahlfors–Bers. IV (Contemporary Mathematics, 432) . American Mathematical Society, Providence, RI, 2007, pp. 45–61.Google Scholar
Hartman, P.. On homotopic harmonic maps. Canad. J. Math. 19 (1967), 673–687.Google Scholar
Hopf, H.. Differential Geometry in The Large (Lecture Notes in Mathematics, 1000) . Springer, Berlin, 1954.Google Scholar
Huang, Z. and Wang, B.. On almost-Fuchsian manifolds. Trans. Amer. Math. Soc. 365(9) (2013), 4679–4698.Google Scholar
Jost, J., Li-Jost, X. and Peng, X. W.. Bifurcation of minimal surfaces in Riemannian manifolds. Trans. Amer. Math. Soc. 347(1) (1995), 51–62.Google Scholar
Katok, A.. Entropy and closed geodesics. Ergod. Th. & Dynam. Sys. 2(3–4) (1982), 339–365; 1983.CrossRefGoogle Scholar
Katok, A. and Hasselblatt, B.. Introduction to The Modern Theory of Dynamical Systems (Encyclopedia of Mathematics and its Applications, 54) . Cambridge University Press, Cambridge, 1995; with a supplementary chapter by Katok and Leonardo Mendoza.Google Scholar
Katok, A., Knieper, G. and Weiss, H.. Formulas for the derivative and critical points of topological entropy for Anosov and geodesic flows. Comm. Math. Phys. 138(1) (1991), 19–31.Google Scholar
Kodaira, K.. Complex Manifolds and Deformation of Complex Structures (Classics in Mathematics) . english edition. Springer, Berlin, 2005; translated from the 1981 Japanese original by Kazuo Akao.Google Scholar
Labourie, F.. Cross ratios, Anosov representations and the energy functional on Teichmüller space. Ann. Sci. Éc. Norm. Supér. (4) 41(3) (2008), 437–469.Google Scholar
Manning, A.. Topological entropy for geodesic flows. Ann. of Math. (2) 110(3) (1979), 567–573.Google Scholar
Manning, A.. Curvature bounds for the entropy of the geodesic flow on a surface. J. Lond. Math. Soc. 24 (1981).Google Scholar
Margulis, G. A.. On Some Aspects of the Theory of Anosov Systems (Springer Monographs in Mathematics) . Springer, Berlin, 2004; with a survey by Richard Sharp: Periodic orbits of hyperbolic flows, translated from the Russian by Valentina Vladimirovna Szulikowska.Google Scholar
McMullen, C. T.. Thermodynamics, dimension and the Weil–Petersson metric. Invent. Math. 173(2) (2008), 365–425.CrossRefGoogle Scholar
Mese, C.. The curvature of minimal surfaces in singular spaces. Comm. Anal. Geom. 9(1) (2001), 3–34.Google Scholar
Meeks III, W., Simon, L. and Yau, S. T.. Embedded minimal surfaces, exotic spheres, and manifolds with positive Ricci curvature. Ann. of Math. (2) 116(3) (1982), 621–659.Google Scholar
Meeks, III, W. W. and Yau, S. T.. The existence of embedded minimal surfaces and the problem of uniqueness. Math. Z. 179(2) (1982), 151–168.Google Scholar
Patterson, S. J.. The limit set of a Fuchsian group. Acta Math. 136(3–4) (1976), 241–273.Google Scholar
Pollicott, M.. Derivatives of topological entropy for Anosov and geodesic flows. J. Differential Geom. 39(3) (1994), 457–489.Google Scholar
Schoen, R.. Estimates for stable minimal surfaces in three-dimensional manifolds. Seminar on Minimal Submanifolds (Annals of Mathematical Studies, 103) . Princeton University Press, Princeton, NJ, 1983, pp. 111–126.Google Scholar
Sacks, J. and Uhlenbeck, K.. Minimal immersions of closed Riemann surfaces. Amer. Math. Soc. 271(2) (1982), 639–652.Google Scholar
Sullivan, D.. Entropy, Hausdorff measures old and new, and limit sets of geometrically finite Kleinian groups. Acta Math. 153(3–4) (1984), 259–277.Google Scholar
Taubes, C. H.. Minimal surfaces in germs of hyperbolic 3-manifolds. Proceedings of the Casson Fest, Geom. Topol. Monogr. 7 (2004), 69–100 (electronic).Google Scholar
Tromba, A. J.. Teichmüller Theory in Riemannian Geometry (Lectures in Mathematics, ETH Zürich) . Birkhäuser Verlag, Basel, 1992; lecture notes prepared by Jochen Denzler.CrossRefGoogle Scholar
Uhlenbeck, K. K.. Closed minimal surfaces in hyperbolic 3-manifolds. Ann. of Math. Stud. 103 (1983), 147–168.Google Scholar
Wolpert, S. A.. Families of Riemann Surfaces and Weil–Petersson Geometry (CBMS Regional Conference Series in Mathematics, 113) . Published for the Conference Board of the Mathematical Sciences, Washington, DC, 2010.Google Scholar