Published online by Cambridge University Press: 19 September 2016
For a given topological dynamical system 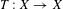 $T:X\rightarrow X$ over a compact set
$T:X\rightarrow X$ over a compact set 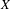 $X$ with a metric
$X$ with a metric 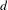 $d$, the variational principle states that
$d$, the variational principle states that 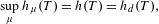 $$\begin{eqnarray}\sup _{\unicode[STIX]{x1D707}}h_{\unicode[STIX]{x1D707}}(T)=h(T)=h_{d}(T),\end{eqnarray}$$
$$\begin{eqnarray}\sup _{\unicode[STIX]{x1D707}}h_{\unicode[STIX]{x1D707}}(T)=h(T)=h_{d}(T),\end{eqnarray}$$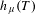 $h_{\unicode[STIX]{x1D707}}(T)$ is the Kolmogorov–Sinai entropy with the supremum taken over every
$h_{\unicode[STIX]{x1D707}}(T)$ is the Kolmogorov–Sinai entropy with the supremum taken over every  $T$-invariant probability measure,
$T$-invariant probability measure, 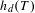 $h_{d}(T)$ is the Bowen entropy and
$h_{d}(T)$ is the Bowen entropy and 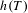 $h(T)$ is the topological entropy as defined by Adler, Konheim and McAndrew. In Patrão [Entropy and its variational principle for non-compact metric spaces. Ergod. Th. & Dynam. Sys. 30 (2010), 1529–1542], the concept of topological entropy was adapted for the case where
$h(T)$ is the topological entropy as defined by Adler, Konheim and McAndrew. In Patrão [Entropy and its variational principle for non-compact metric spaces. Ergod. Th. & Dynam. Sys. 30 (2010), 1529–1542], the concept of topological entropy was adapted for the case where  $T$ is a proper map and
$T$ is a proper map and 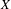 $X$ is locally compact separable and metrizable, and the variational principle was extended to
$X$ is locally compact separable and metrizable, and the variational principle was extended to 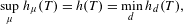 $$\begin{eqnarray}\sup _{\unicode[STIX]{x1D707}}h_{\unicode[STIX]{x1D707}}(T)=h(T)=\min _{d}h_{d}(T),\end{eqnarray}$$
$$\begin{eqnarray}\sup _{\unicode[STIX]{x1D707}}h_{\unicode[STIX]{x1D707}}(T)=h(T)=\min _{d}h_{d}(T),\end{eqnarray}$$ $X$. In the present work, we drop the properness assumption and extend the above result for any continuous map
$X$. In the present work, we drop the properness assumption and extend the above result for any continuous map  $T$. We also apply our results to extend some previous formulae for the topological entropy of continuous endomorphisms of connected Lie groups that were proved in Caldas and Patrão [Dynamics of endomorphisms of Lie groups. Discrete Contin. Dyn. Syst. 33 (2013). 1351–1363]. In particular, we prove that any linear transformation
$T$. We also apply our results to extend some previous formulae for the topological entropy of continuous endomorphisms of connected Lie groups that were proved in Caldas and Patrão [Dynamics of endomorphisms of Lie groups. Discrete Contin. Dyn. Syst. 33 (2013). 1351–1363]. In particular, we prove that any linear transformation 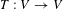 $T:V\rightarrow V$ over a finite-dimensional vector space
$T:V\rightarrow V$ over a finite-dimensional vector space  $V$ has null topological entropy.
$V$ has null topological entropy.