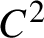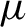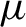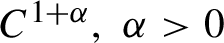Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Zang, Yuntao
2022.
An upper bound of the measure-theoretical entropy.
Discrete and Continuous Dynamical Systems,
Vol. 42,
Issue. 9,
p.
4263.
Buzzi, Jérôme
Crovisier, Sylvain
and
Sarig, Omri
2022.
Continuity properties of Lyapunov exponents for surface diffeomorphisms.
Inventiones mathematicae,
Vol. 230,
Issue. 2,
p.
767.
Yang, Dawei
and
Zang, Yuntao
2023.
Volume growth and topological entropy of partially hyperbolic systems.
Israel Journal of Mathematics,
Vol. 255,
Issue. 1,
p.
325.
Chen, Yexing
Cao, Yongluo
and
Zang, Yuntao
2024.
Katok's entropy formula of unstable metric entropy for random dynamical systems.
Journal of Mathematical Analysis and Applications,
Vol. 531,
Issue. 1,
p.
127864.