Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-24T16:30:16.288Z Has data issue: false hasContentIssue false
  • English
  • Français

Effectivity of uniqueness of the maximal entropy measure on 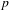$p$ -adic homogeneous spaces

Published online by Cambridge University Press:  11 February 2015

RENE RÜHR Open the ORCID record for RENE RÜHR [Opens in a new window]
RENE RÜHR*
Affiliation:
Eidgenössische Technische Hochschule Zürich, Rämistrasse 101, 8092 Zürich, Switzerland email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider the dynamical system given by an 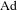$\text{Ad}$ -diagonalizable element $a$ of the 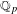$\mathbb{Q}_{p}$ -points $G$ of a unimodular linear algebraic group acting by translation on a finite volume quotient 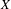$X$ . Assuming that this action is exponentially mixing (e.g. if 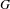$G$ is simple) we give an effective version (in terms of 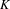$K$ -finite vectors of the regular representation) of the following statement: If 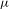${\it\mu}$ is an $a$ -invariant probability measure with measure-theoretical entropy close to the topological entropy of $a$ , then 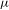${\it\mu}$ is close to the unique 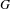$G$ -invariant probability measure of 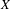$X$ .

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 36 , Issue 6 , September 2016 , pp. 1972 - 1988
Copyright
© Cambridge University Press, 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adler, R. L. and Weiss, B.. Entropy, a complete metric invariant for automorphisms of the torus. Proc. Natl Acad. Sci. USA 57 (1967), 1573–1576.Google Scholar
Bowen, R.. Entropy for group endomorphisms and homogeneous spaces. Trans. Amer. Math. Soc. 153 (1971), 401–414.Google Scholar
Borel, A. and Wallach, N.. Continuous Cohomology, Discrete Subgroups, and Representations of Reductive Groups (Mathematical Surveys and Monographs, 67) , 2nd edn. American Mathematical Society, Providence, RI, 2000.Google Scholar
Cowling, M., Haagerup, U. and Howe, R.. Almost L 2 matrix coefficients. J. Reine Angew. Math. 387 (1988), 97–110.Google Scholar
Cowling, M.. Sur les coefficients des représentations unitaires des groupes de Lie simples. Analyse Harmonique sur les Groupes de Lie (Sém., Nancy-Strasbourg 1976–1978, II) (Lecture Notes in Mathematics, 739) . Springer, Berlin, 1979, pp. 132–178.Google Scholar
Cover, T. M. and Thomas, J. A.. Elements of Information Theory (Wiley Series in Telecommunications) . Wiley, New York, 1991.Google Scholar
Einsiedler, M., Katok, A. and Lindenstrauss, E.. Invariant measures and the set of exceptions to Littlewood’s conjecture. Ann. of Math. (2) 164(2) (2006), 513–560.Google Scholar
Einsiedler, M. and Lindenstrauss, E.. Diagonal actions on locally homogeneous spaces. Homogeneous Flows, Moduli Spaces and Arithmetic (Clay Mathematics Monographs, 10) . American Mathematical Society, Providence, RI, 2010, pp. 155–241.Google Scholar
Einsiedler, M. and Ward, T.. Ergodic Theory with a View Towards Number Theory (Graduate Texts in Mathematics, 259) . Springer, London, 2011.Google Scholar
Howe, R. E. and Moore, C. C.. Asymptotic properties of unitary representations. J. Funct. Anal. 32(1) (1979), 72–96.Google Scholar
Howe, R. and Tan, E.-C.. Non-Abelian Harmonic Analysis: Applications of SL (2, R) (Universitext) . Springer, New York, 1992.Google Scholar
Kadyrov, S.. Effective uniqueness of Parry measure and exceptional sets in ergodic theory. Monatsh. Math. (2014), to appear, doi:10.1007/s00605-014-0690-7.Google Scholar
Margulis, G. A.. Discrete Subgroups of Semisimple Lie Groups (Ergebnisse der Mathematik und ihrer Grenzgebiete (3) [Results in Mathematics and Related Areas (3)], 17) . Springer, Berlin, 1991.Google Scholar
Margulis, G. A. and Tomanov, G. M.. Invariant measures for actions of unipotent groups over local fields on homogeneous spaces. Invent. Math. 116(1–3) (1994), 347–392.Google Scholar
Oh, H.. Uniform pointwise bounds for matrix coefficients of unitary representations and applications to Kazhdan constants. Duke Math. J. 113(1) (2002), 133–192.CrossRefGoogle Scholar
Polo, F.. Equidistribution in chaotic dynamical systems. PhD Thesis, The Ohio State University, 2011.Google Scholar
Platonov, V. and Rapinchuk, A.. Algebraic Groups and Number Theory (Pure and Applied Mathematics, 139) . Academic Press, Boston, MA, 1994; translated from the 1991 Russian original by Rachel Rowen.Google Scholar
Ratner, M.. On the p-adic and S-arithmetic generalizations of Raghunathan’s conjectures. Lie Groups and Ergodic Theory (Mumbai, 1996) (Tata Institute of Fundamental Research Studies in Mathematics, 14) . Tata Institute of Fundamental Research, Bombay, 1998, pp. 167–202.Google Scholar
Serre, J.-P.. Lie Algebras and Lie Groups: 1964 Lectures given at Harvard University (Lecture Notes in Mathematics, 1500) , 2nd edn. Springer, Berlin, 1992.CrossRefGoogle Scholar
Shalom, Y.. Rigidity, unitary representations of semisimple groups, and fundamental groups of manifolds with rank one transformation group. Ann. of Math. (2) 152(1) (2000), 113–182.Google Scholar
Silberger, A. J.. Introduction to Harmonic Analysis on Reductive p-adic Groups (Mathematical Notes, 23) . Princeton University Press, Princeton, NJ, 1979, pp. 1971–1973; based on lectures by Harish-Chandra at the Institute for Advanced Study.Google Scholar