No CrossRef data available.
Published online by Cambridge University Press: 12 December 2017
Using quantitative perturbation theory for linear operators, we prove a spectral gap for transfer operators of various families of intermittent maps with almost constant potentials (‘high-temperature’ regime). Hölder and bounded 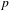 $p$-variation potentials are treated, in each case under a suitable assumption on the map, but the method should apply more generally. It is notably proved that for any Pommeau–Manneville map, any potential with Lipschitz constant less than 0.0014 has a transfer operator acting on
$p$-variation potentials are treated, in each case under a suitable assumption on the map, but the method should apply more generally. It is notably proved that for any Pommeau–Manneville map, any potential with Lipschitz constant less than 0.0014 has a transfer operator acting on 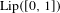 $\operatorname{Lip}([0,1])$ with a spectral gap; and that for any two-to-one unimodal map, any potential with total variation less than 0.0069 has a transfer operator acting on
$\operatorname{Lip}([0,1])$ with a spectral gap; and that for any two-to-one unimodal map, any potential with total variation less than 0.0069 has a transfer operator acting on 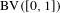 $\operatorname{BV}([0,1])$ with a spectral gap. We also prove under quite general hypotheses that the classical definition of spectral gap coincides with the formally stronger one used in Giulietti et al [The calculus of thermodynamical formalism. J. Eur. Math. Soc., to appear. Preprint, 2015, arXiv:1508.01297], allowing all results there to be applied under the high-temperature bounds proved here: analyticity of pressure and equilibrium states, central limit theorem, etc.
$\operatorname{BV}([0,1])$ with a spectral gap. We also prove under quite general hypotheses that the classical definition of spectral gap coincides with the formally stronger one used in Giulietti et al [The calculus of thermodynamical formalism. J. Eur. Math. Soc., to appear. Preprint, 2015, arXiv:1508.01297], allowing all results there to be applied under the high-temperature bounds proved here: analyticity of pressure and equilibrium states, central limit theorem, etc.