Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-26T01:04:45.906Z Has data issue: false hasContentIssue false
  • English
  • Français

Dynamics of quasiregular mappings with constant complex dilatation

Published online by Cambridge University Press:  21 November 2014

ALASTAIR FLETCHER  and
ROB FRYER
ALASTAIR FLETCHER
Affiliation:
Department of Mathematical Sciences, Northern Illinois University, DeKalb, IL 60115-2888, USA email [email protected], [email protected]
ROB FRYER
Affiliation:
Department of Mathematical Sciences, Northern Illinois University, DeKalb, IL 60115-2888, USA email [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The study of quadratic polynomials is a foundational part of modern complex dynamics. In this article, we study quasiregular counterparts to these in the plane. More specifically, let 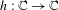$h:\mathbb{C}\rightarrow \mathbb{C}$ be an 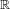$\mathbb{R}$-linear map and consider the quasiregular mapping 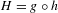$H=g\circ h$, where $g$ is a quadratic polynomial. By studying 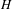$H$ and via the Böttcher-type coordinate constructed in A. Fletcher and R. Fryer [On Böttcher coordinates and quasiregular maps. Contemp. Math.575 (2012), 53–76], we are able to obtain results on the dynamics of any degree-two mapping of the plane with constant complex dilatation. We show that any such mapping has either one, two or three fixed external rays, that all cases can occur and exhibit how the dynamics changes in each case. We use results from complex dynamics to prove that these mappings are nowhere uniformly quasiregular in a neighbourhood of infinity. We also show that in most cases, two such mappings are not quasiconformally conjugate on a neighbourhood of infinity.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 36 , Issue 2 , April 2016 , pp. 514 - 549
Copyright
© Cambridge University Press, 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bergweiler, W.. Iteration of quasiregular mappings. Comput. Methods Funct. Theory 10 (2010), 455–481.CrossRefGoogle Scholar
Bergweiler, W.. Fatou–Julia theory for non-uniformly quasiregular maps. Ergod. Th. & Dynam. Sys. 33 (2013), 1–23.CrossRefGoogle Scholar
Bielefeld, B., Sutherland, S., Tangerman, F. and Veerman, J. J. P.. Dynamics of certain nonconformal degree-two maps of the plane. Exp. Math. 2(4) (1993), 281–300.CrossRefGoogle Scholar
Bozyk, B. and Peckham, B. B.. Dynamics of nonholomorphic singular continuations: a case in radial symmetry. Internat. J. Bifur. Chaos Appl. Sci. Engrg. 23(11) (2013), 1–22.CrossRefGoogle Scholar
Bruin, H. and van Noort, M.. Nonconformal perturbations of z↦z 2 + c: the 1 : 3 resonance. Nonlinearity 17(3) (2004), 765–789.CrossRefGoogle Scholar
Carleson, L. and Gamelin, T.. Complex Dynamics. Springer, New York, 1993.CrossRefGoogle Scholar
Fletcher, A. and Fryer, R.. On Böttcher coordinates and quasiregular maps. Quasiconformal Mappings, Riemann Surfaces, and Teichmüller Spaces (Contempoary Mathematics, 575). American Mathematical Society, Providence, RI, 2012, pp. 53–76.CrossRefGoogle Scholar
Fletcher, A. and Goodman, D.. Quasiregular mappings of polynomial type in ℝ2. Conform. Geom. Dyn. 14 (2010), 322–336.CrossRefGoogle Scholar
Fletcher, A. and Markovic, V.. Quasiconformal Mappings and Teichmüller Spaces. Oxford University Press, Oxford, 2007.Google Scholar
Fletcher, A. and Nicks, D. A.. Quasiregular dynamics on the n-sphere. Ergod. Th. & Dynam. Sys. 31 (2011), 23–31.CrossRefGoogle Scholar
Gill, J.. Outer compositions of hyperbolic/loxodromic linear fractional transformations. Internat. J. Math. Math. Sci. 15(4) (1992), 819–822.CrossRefGoogle Scholar
Hinkkanen, A.. Uniformly quasiregular semigroups in two dimensions. Ann. Acad. Sci. Fenn. 21(1) (1996), 205–222.Google Scholar
Iwaniec, T. and Martin, G.. Quasiregular semigroups. Ann. Acad. Sci. Fenn. 21(2) (1996), 241–254.Google Scholar
Jiang, Y.. Dynamics of certain nonconformal semigroups. Complex Var. Theory Appl. 22(1–2) (1993), 27–34.Google Scholar
Mandell, M. and Magnus, A.. On convergence of sequences of linear fractional transformations. Math. Z. 115 (1970), 11–17.CrossRefGoogle Scholar
Milnor, J.. Dynamics in One Complex Variable (Annals of Mathematics Studies, 160), 3rd edn. Princeton University Press, Princeton, NJ, 2006.Google Scholar
Peckham, B. B.. Real perturbation of complex analytic families: points to regions. Internat. J. Bifur. Chaos Appl. Sci. Engrg. 8(1) (1998), 73–93.CrossRefGoogle Scholar
Peckham, B. B. and Montaldi, J.. Real continuation from the complex quadratic family: fixed-point bifurcation sets. Internat. J. Bifur. Chaos Appl. Sci. Engrg. 10(2) (2000), 391–414.CrossRefGoogle Scholar
Rickman, S.. Quasiregular Mappings (Ergebnisse der Mathematik und ihrer Grenzgebiete, 26). Springer, Berlin, 1993.CrossRefGoogle Scholar
Szczyrek, J. J.. Hausdorff dimension of a limit set for a family of nonholomorphic perturbations of the map z↦z 2. Nonlinearity 12(5) (1999), 1439–1448.CrossRefGoogle Scholar