Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-27T02:01:48.012Z Has data issue: false hasContentIssue false
  • English
  • Français

Dynamics of post-critically finite maps in higher dimension

Published online by Cambridge University Press:  06 July 2018

MATTHIEU ASTORG
MATTHIEU ASTORG*
Affiliation:
Université d’Orléans, Collegium Sciences et Techniques, Bâtiment de mathématiques – Rue de Chartres, B.P. 6759 – 45067 Orléans Cedex 2, France email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the dynamics of post-critically finite endomorphisms of 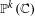$\mathbb{P}^{k}(\mathbb{C})$. We prove that post-critically finite endomorphisms are always post-critically finite all the way down under a regularity condition on the post-critical set. We study the eigenvalues of periodic points of post-critically finite endomorphisms. Then, under a transversality condition and assuming Kobayashi hyperbolicity of the complement of the post-critical set, we prove that the only possible Fatou components are super-attracting basins; thus, partially extending to any dimension is a result of Fornaess–Sibony and Rong holding in the case 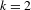$k=2$.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 40 , Issue 2 , February 2020 , pp. 289 - 308
Copyright
© Cambridge University Press, 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Astorg, M., Buff, X., Dujardin, R., Peters, H. and Raissy, J.. A two-dimensional polynomial mapping with a wandering Fatou component. Ann. of Math. (2) 184(1) (2016), 263–313.Google Scholar
Cartan, H.. Sur les rétractions d’une variété. C.R. Acad. Sci. Paris Sér. I Math. 303 (1986), 715–716.Google Scholar
Douady, A. and Hubbard, J. J.. A proof of Thurston’s topological characterization of rational functions. Acta Math. 171(2) (1993), 263–297.Google Scholar
Dinh, T.-C. and Sibony, N.. Dynamics in several complex variables: endomorphisms of projective spaces and polynomial-like mappings. Holomorphic Dynamical Systems (Lecture Notes in Mathematics, 1998) . Springer, Berlin, 2010, pp. 165–294.Google Scholar
De Thélin, H.. Un phénomène de concentration de genre. Math. Ann. 332(3) (2005), 483–498.Google Scholar
Fornæss, J. and Sibony, N.. Critically finite rational maps on ℙ2 . The Madison Symposium on Complex Analysis: Proceedings of the Symposium on Complex Analysis, 2–7 June 1991, University of Wisconsin–Madison (Contemporary Mathematics, 137) . American Mathematical Society, Providence, RI, 1992, p. 245.Google Scholar
Fornæss, J. E. and Sibony, N.. Complex dynamics in higher dimension I. Complex Analytic Methods in Dynamical Systems (Rio de Janeiro, 1992). Astérisque 5(222) (1994), 201–231.Google Scholar
Gauthier, T., Hutz, B. and Kaschner, S.. Symmetrization of rational maps: arithmetic properties and families of Lattès maps of $\mathbb{P}^{k}$ . Preprint, 2016, arXiv:1603.04887.Google Scholar
Grauert, H., Remmert, R. and Räume, K.. Math. Ann. 136(3) (1958), 245–318.Google Scholar
Jonsson, M.. Some properties of 2-critically finite holomorphic maps of ℙ2 . Ergod. Th. & Dynam. Sys. 18(01) (1998), 171–187.Google Scholar
Koch, S.. Teichmüller theory and critically finite endomorphisms. Adv. Math. 248 (2013), 573–617.Google Scholar
Rong, F.. The Fatou set for critically finite maps. Proc. Amer. Math. Soc. 136(10) (2008), 3621–3625.Google Scholar
Thurston, W. P.. On the Combinatorics of Iterated Rational Maps. Princeton University, 1985.Google Scholar
Ueda, T.. Critical orbits of holomorphic maps on projective spaces. J. Geom. Anal. 8(2) (1998), 319–334.Google Scholar