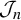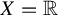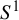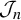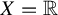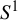1 Introduction
Iteration of a map is a composition of the map and itself. More precisely, the nth order iterate of a map
![]() $f: X\to X$
on a non-empty set X, denoted by
$f: X\to X$
on a non-empty set X, denoted by
![]() $f^n$
, is defined inductively by
$f^n$
, is defined inductively by
![]() $f^n=f\circ f^{n-1}$
and
$f^n=f\circ f^{n-1}$
and
![]() $f^0=\mathrm {id}$
, the identity map. As known in [Reference Blokh5, Reference Milnor, Thurston and Alexander20], iteration is one of the most important operations in contemporary mathematics because the dynamical system theory is based on iteration, numerical computation needs iteration, and all computer loop programs are iteration. Thus, iteration has attracted interests of research for a long time (see e.g. [Reference Babbage2, Reference Blokh5, Reference Bödewadt6, Reference Fort9, Reference Jarczyk11, Reference Kuczma13, Reference Kuczma14, Reference Milnor, Thurston and Alexander20, Reference Zhang27]).
$f^0=\mathrm {id}$
, the identity map. As known in [Reference Blokh5, Reference Milnor, Thurston and Alexander20], iteration is one of the most important operations in contemporary mathematics because the dynamical system theory is based on iteration, numerical computation needs iteration, and all computer loop programs are iteration. Thus, iteration has attracted interests of research for a long time (see e.g. [Reference Babbage2, Reference Blokh5, Reference Bödewadt6, Reference Fort9, Reference Jarczyk11, Reference Kuczma13, Reference Kuczma14, Reference Milnor, Thurston and Alexander20, Reference Zhang27]).
Consider iteration of function f in a space
![]() $\mathcal {X}$
of functions and let
$\mathcal {X}$
of functions and let
![]() $\mathcal {J}_n$
denote the correspondence
$\mathcal {J}_n$
denote the correspondence
called the nth order iteration operator. This operator was proved to be continuous on
![]() $\mathcal {X}:=\mathcal {C}([a,b])$
, the space of continuous self-maps of a compact interval, in [Reference Zhang and Zhang28], and later on
$\mathcal {X}:=\mathcal {C}([a,b])$
, the space of continuous self-maps of a compact interval, in [Reference Zhang and Zhang28], and later on
![]() $\mathcal {C}(X)$
with a general compact metric space X in [Reference Veerapazham, Gopalakrishna and Zhang23]. Furthermore, the authors [Reference Veerapazham, Gopalakrishna and Zhang23] considered the semi-dynamical system
$\mathcal {C}(X)$
with a general compact metric space X in [Reference Veerapazham, Gopalakrishna and Zhang23]. Furthermore, the authors [Reference Veerapazham, Gopalakrishna and Zhang23] considered the semi-dynamical system
![]() $(\mathcal {C}(X),\mathcal {J}_n)$
generated by
$(\mathcal {C}(X),\mathcal {J}_n)$
generated by
![]() $\mathcal {J}_n$
, which is the iteration semigroup
$\mathcal {J}_n$
, which is the iteration semigroup
![]() $\{\mathcal {J}_n^k: k=0,1,\ldots \}$
, and discussed its periodic points. They computed periodic points for
$\{\mathcal {J}_n^k: k=0,1,\ldots \}$
, and discussed its periodic points. They computed periodic points for
![]() $X=[a,b]$
, gave boundedness of orbits and instability of the fixed points which are identity on their range in
$X=[a,b]$
, gave boundedness of orbits and instability of the fixed points which are identity on their range in
![]() $\mathcal {C}([a,b])$
, and proved that
$\mathcal {C}([a,b])$
, and proved that
![]() $\mathcal {J}_n$
is not topologically transitive in
$\mathcal {J}_n$
is not topologically transitive in
![]() $\mathcal {C}(X)$
with a compact metric space X. They showed that
$\mathcal {C}(X)$
with a compact metric space X. They showed that
![]() $\mathcal {J}_n$
is not chaotic in Devaney’s sense although boundedness with instability exhibits a complicated behavior.
$\mathcal {J}_n$
is not chaotic in Devaney’s sense although boundedness with instability exhibits a complicated behavior.
In addition to the case that X is a compact interval, it is also interesting to discuss dynamics of iteration operators for
![]() $X=S^1$
(the unit circle in
$X=S^1$
(the unit circle in
![]() $\mathbb {C}$
), a compact space without boundary,
$\mathbb {C}$
), a compact space without boundary,
![]() $X=\mathbb {R}$
without compactness, and more generally a locally compact Hausdorff space X, which can be a space of p-adic numbers (metrizable) or a manifold (not necessarily metrizable). So, we will generally consider X to be a locally compact Hausdorff space (not necessarily metrizable) and let
$X=\mathbb {R}$
without compactness, and more generally a locally compact Hausdorff space X, which can be a space of p-adic numbers (metrizable) or a manifold (not necessarily metrizable). So, we will generally consider X to be a locally compact Hausdorff space (not necessarily metrizable) and let
![]() $\mathcal {C}(X):={C}^0(X,X)$
consist of all continuous self-maps of X, which is not necessarily a metric space but a topological space in the compact-open topology as shown in §2. We want to know what dynamical behaviors of an iteration operator are common for a general locally compact Hausdorff space X and what properties of an iteration operator in a specified X are not shared in another.
$\mathcal {C}(X):={C}^0(X,X)$
consist of all continuous self-maps of X, which is not necessarily a metric space but a topological space in the compact-open topology as shown in §2. We want to know what dynamical behaviors of an iteration operator are common for a general locally compact Hausdorff space X and what properties of an iteration operator in a specified X are not shared in another.
In this paper, we discuss dynamical behaviors of the semi-dynamical system
![]() $(\mathcal {C}(X),\mathcal {J}_n)$
for X to be a locally compact Hausdorff space. After making preliminaries on locally compact Hausdorff spaces X in §2, we prove continuity of the iteration operator
$(\mathcal {C}(X),\mathcal {J}_n)$
for X to be a locally compact Hausdorff space. After making preliminaries on locally compact Hausdorff spaces X in §2, we prove continuity of the iteration operator
![]() $\mathcal {J}_n$
on
$\mathcal {J}_n$
on
![]() $\mathcal {C}(X)$
, which is the same as given in [Reference Veerapazham, Gopalakrishna and Zhang23] for compact metric spaces X but for which we use a different tool ‘iterated evaluation map’ in the proof, and investigate periodic points of
$\mathcal {C}(X)$
, which is the same as given in [Reference Veerapazham, Gopalakrishna and Zhang23] for compact metric spaces X but for which we use a different tool ‘iterated evaluation map’ in the proof, and investigate periodic points of
![]() $\mathcal {J}_n$
in
$\mathcal {J}_n$
in
![]() $\mathcal {C}(\mathbb {R})$
and
$\mathcal {C}(\mathbb {R})$
and
![]() $\mathcal {C}(S^1)$
in §3. We characterize all fixed points and periodic points of the system by discussing the Babbage equation, part of which looks similar to those of [Reference Veerapazham, Gopalakrishna and Zhang23] but their applicability is enhanced to a larger extent. We show that in
$\mathcal {C}(S^1)$
in §3. We characterize all fixed points and periodic points of the system by discussing the Babbage equation, part of which looks similar to those of [Reference Veerapazham, Gopalakrishna and Zhang23] but their applicability is enhanced to a larger extent. We show that in
![]() $\mathcal {C}(S^1)$
, each
$\mathcal {C}(S^1)$
, each
![]() ${\cal J}_n$
may have periodic points of period
${\cal J}_n$
may have periodic points of period
![]() $k\ge 2$
, whereas in
$k\ge 2$
, whereas in
![]() $\mathcal {C}(\mathbb {R})$
, each
$\mathcal {C}(\mathbb {R})$
, each
![]() ${\cal J}_n$
only has fixed points. In §4, we discuss the stability for
${\cal J}_n$
only has fixed points. In §4, we discuss the stability for
![]() $\mathcal {J}_n$
. First, we generally note that all orbits of
$\mathcal {J}_n$
. First, we generally note that all orbits of
![]() $\mathcal {J}_n$
are bounded. Then we prove that in
$\mathcal {J}_n$
are bounded. Then we prove that in
![]() $\mathcal {C}(\mathbb {R})$
and
$\mathcal {C}(\mathbb {R})$
and
![]() $\mathcal {C}(S^1)$
, every fixed point of
$\mathcal {C}(S^1)$
, every fixed point of
![]() $\mathcal {J}_n$
which is non-constant and equals the identity on its range is not Lyapunov stable. The boundedness and the instability exhibit the complexity of the system, but we observe that the complicated behavior is not Devaney chaotic. In §5, we give a sufficient condition to classify the systems generated by iteration operators up to topological conjugacy and prove that
$\mathcal {J}_n$
which is non-constant and equals the identity on its range is not Lyapunov stable. The boundedness and the instability exhibit the complexity of the system, but we observe that the complicated behavior is not Devaney chaotic. In §5, we give a sufficient condition to classify the systems generated by iteration operators up to topological conjugacy and prove that
![]() $(\mathcal {C}(X), \mathcal {J}_2)$
is not conjugate to
$(\mathcal {C}(X), \mathcal {J}_2)$
is not conjugate to
![]() $(\mathcal {C}(Y), \mathcal {J}_m)$
for every locally compact Hausdorff space Y and odd positive integer m whenever
$(\mathcal {C}(Y), \mathcal {J}_m)$
for every locally compact Hausdorff space Y and odd positive integer m whenever
![]() $\mathcal {C}(X)$
contains an involutory map different from
$\mathcal {C}(X)$
contains an involutory map different from
![]() $\mathrm {id}$
. Finally, we give some remarks and leave some questions for future discussion in §6.
$\mathrm {id}$
. Finally, we give some remarks and leave some questions for future discussion in §6.
2 Preliminaries
In this section, we give some preliminaries for locally compact Hausdorff spaces, which we will work on in this paper. Unless mentioned particularly, let
![]() $X, Y, Z$
denote topological spaces and
$X, Y, Z$
denote topological spaces and
![]() $C(X,Y)$
the set of all continuous maps of X into Y. Define on
$C(X,Y)$
the set of all continuous maps of X into Y. Define on
![]() ${C}(X, Y)$
the compact-open topology (see [Reference Munkres21, p. 285]), that is, the topology generated by the collection of all finite intersections of sets in
${C}(X, Y)$
the compact-open topology (see [Reference Munkres21, p. 285]), that is, the topology generated by the collection of all finite intersections of sets in
where
![]() $\mathcal {F}(K,U):=\{f\in {C}(X, Y):f(K)\subseteq U\}$
. When Y is a metric space equipped with metric d, we have another topology on
$\mathcal {F}(K,U):=\{f\in {C}(X, Y):f(K)\subseteq U\}$
. When Y is a metric space equipped with metric d, we have another topology on
![]() ${C}(X,Y)$
, viz. the topology of compact convergence generated by
${C}(X,Y)$
, viz. the topology of compact convergence generated by
where
![]() $\mathcal {B}_K(f,\epsilon ):=\{g\in {C}(X,Y): \sup \{d(f(x), g(x)):x\in K\}<\epsilon \}$
.
$\mathcal {B}_K(f,\epsilon ):=\{g\in {C}(X,Y): \sup \{d(f(x), g(x)):x\in K\}<\epsilon \}$
.
Lemma 1
-
(i) [Reference Munkres21, Theorem 46.7, p. 285] If X is a compact space and Y a metric space with metric d, then on
 ${C}(X,Y)$
, the uniform topology induced by the metric
${C}(X,Y)$
, the uniform topology induced by the metric
 $\rho (f,g):=\sup \{d(f(x),g(x)): x\in X\}$
and the topology of compact convergence coincide.
$\rho (f,g):=\sup \{d(f(x),g(x)): x\in X\}$
and the topology of compact convergence coincide. -
(ii) [Reference Munkres21, Theorem 46.8, p. 285] If Y is a metric space with metric d, then on
 ${C}(X,Y)$
, the compact-open topology and the topology of compact convergence coincide.
${C}(X,Y)$
, the compact-open topology and the topology of compact convergence coincide.
Lemma 2. [Reference Munkres21, Theorem 46.10, p. 286]
If X is locally compact Hausdorff and
![]() ${C}(X, Y)$
have the compact-open topology, then the evaluation map
${C}(X, Y)$
have the compact-open topology, then the evaluation map
![]() $\mathcal {E}:X\times {C}(X, Y) \rightarrow Y$
defined by
$\mathcal {E}:X\times {C}(X, Y) \rightarrow Y$
defined by
![]() $\mathcal {E}(x,f)= f(x)$
is continuous.
$\mathcal {E}(x,f)= f(x)$
is continuous.
Lemma 3. [Reference Munkres21, Theorem 46.11, p. 287]
Let
![]() ${C}(X, Y)$
have the compact-open topology. If
${C}(X, Y)$
have the compact-open topology. If
![]() $h: X \times Z\rightarrow Y$
is continuous, then so is its induced map
$h: X \times Z\rightarrow Y$
is continuous, then so is its induced map
![]() $F:Z \rightarrow C(X, Y)$
defined by
$F:Z \rightarrow C(X, Y)$
defined by
![]() $F(z)(x)= h(x,z)$
.
$F(z)(x)= h(x,z)$
.
As defined in [Reference Arens1], a topological space X is said to be hemicompact if there exists a sequence
![]() $(K_j)_{j\in \mathbb {N}}$
of compact sets of X such that if K is any compact subset of X, then
$(K_j)_{j\in \mathbb {N}}$
of compact sets of X such that if K is any compact subset of X, then
![]() $K\subseteq \bigcup _{i=1}^{k}K_{m_i}$
for some finitely many
$K\subseteq \bigcup _{i=1}^{k}K_{m_i}$
for some finitely many
![]() $K_{m_1}, K_{m_2}, \ldots , K_{m_k}$
.
$K_{m_1}, K_{m_2}, \ldots , K_{m_k}$
.
Lemma 4
-
(i) [Reference Arens1, Theorem 7] If X is hemicompact and Y is metrizable, then
 ${C}(X,Y)$
in the compact-open topology is metrizable with metric D given by (2.2)where
${C}(X,Y)$
in the compact-open topology is metrizable with metric D given by (2.2)where $$ \begin{align} D(f,g):=\sum_{j=1}^{\infty}\mu_j(f,g), \end{align} $$
(2.3)
$$ \begin{align} D(f,g):=\sum_{j=1}^{\infty}\mu_j(f,g), \end{align} $$
(2.3) $$ \begin{align} \mu_j(f,g)&:=\min\bigg\{\frac{1}{2^j}, \rho_j(f,g)\bigg\}\quad \text{for all } j\in \mathbb{N}, \end{align} $$
(2.4)with d inducing the topology of Y.
$$ \begin{align} \mu_j(f,g)&:=\min\bigg\{\frac{1}{2^j}, \rho_j(f,g)\bigg\}\quad \text{for all } j\in \mathbb{N}, \end{align} $$
(2.4)with d inducing the topology of Y. $$ \begin{align} \rho_j(f,g)&:=\sup \{d(f(x), g(x)): x\in K_j\}\quad \text{for all } j\in \mathbb{N}, \end{align} $$
$$ \begin{align} \rho_j(f,g)&:=\sup \{d(f(x), g(x)): x\in K_j\}\quad \text{for all } j\in \mathbb{N}, \end{align} $$
-
(ii) [Reference McCoy and Ntantu17, Problem 1, p. 68] If
 ${C}(X, Y)$
in the compact-open topology is metrizable, then X is hemicompact and Y is metrizable.
${C}(X, Y)$
in the compact-open topology is metrizable, then X is hemicompact and Y is metrizable.
3 Continuity and periodic points
Let X be a locally compact Hausdorff space. In this section, we prove
![]() $(\mathcal {C}(X),\mathcal {J}_n)$
to be a discrete semi-dynamical system indeed by showing the continuity of
$(\mathcal {C}(X),\mathcal {J}_n)$
to be a discrete semi-dynamical system indeed by showing the continuity of
![]() $\mathcal {J}_n$
on
$\mathcal {J}_n$
on
![]() $\mathcal {C}(X)$
.
$\mathcal {C}(X)$
.
Theorem 1.
![]() $\mathcal {J}_n$
is continuous on
$\mathcal {J}_n$
is continuous on
![]() $\mathcal {C}(X)$
for each
$\mathcal {C}(X)$
for each
![]() $n\in \mathbb {N}$
.
$n\in \mathbb {N}$
.
Proof. First, we prove by induction that the iterated evaluation map
![]() $\mathcal {E}_n:X\times \mathcal {C}(X)\rightarrow X$
defined by
$\mathcal {E}_n:X\times \mathcal {C}(X)\rightarrow X$
defined by
is continuous on
![]() $X\times \mathcal {C}(X)$
for each
$X\times \mathcal {C}(X)$
for each
![]() $n\in \mathbb {N}$
. The case
$n\in \mathbb {N}$
. The case
![]() $n=1$
follows by Lemma 2, where
$n=1$
follows by Lemma 2, where
![]() $Y=X$
and
$Y=X$
and
![]() $\mathcal {E}_1=\mathcal {E}$
. Suppose that
$\mathcal {E}_1=\mathcal {E}$
. Suppose that
![]() $\mathcal {E}_n$
is continuous for certain
$\mathcal {E}_n$
is continuous for certain
![]() $n\ge 2$
. To prove
$n\ge 2$
. To prove
![]() $\mathcal {E}_{n+1}$
is continuous on
$\mathcal {E}_{n+1}$
is continuous on
![]() $X\times \mathcal {C}(X)$
, consider the map
$X\times \mathcal {C}(X)$
, consider the map
![]() $\mathcal {H}_n:X\times \mathcal {C}(X)\rightarrow X\times \mathcal {C}(X)$
defined by
$\mathcal {H}_n:X\times \mathcal {C}(X)\rightarrow X\times \mathcal {C}(X)$
defined by
![]() $\mathcal {H}_n{\kern-1pt}={\kern-1pt}(\mathcal {E}_n, p)$
, where
$\mathcal {H}_n{\kern-1pt}={\kern-1pt}(\mathcal {E}_n, p)$
, where
![]() $p:X{\kern-1pt}\times{\kern-1pt} \mathcal {C}(X){\kern-1pt}\rightarrow{\kern-1pt} \mathcal {C}(X)$
is the projection map defined by
$p:X{\kern-1pt}\times{\kern-1pt} \mathcal {C}(X){\kern-1pt}\rightarrow{\kern-1pt} \mathcal {C}(X)$
is the projection map defined by
![]() $p(x,f)=f.$
Since
$p(x,f)=f.$
Since
![]() $\mathcal {E}_n$
and p are continuous, so is
$\mathcal {E}_n$
and p are continuous, so is
![]() $\mathcal {H}_n$
. Now,
$\mathcal {H}_n$
. Now,
for each
![]() $(x,f)\in X\times \mathcal {C}(X)$
, implying that
$(x,f)\in X\times \mathcal {C}(X)$
, implying that
![]() $\mathcal {E}_{n+1}=\mathcal {E}\circ \mathcal {H}_n$
. Therefore,
$\mathcal {E}_{n+1}=\mathcal {E}\circ \mathcal {H}_n$
. Therefore,
![]() $\mathcal {E}_{n+1}$
is continuous, being the composition of continuous maps
$\mathcal {E}_{n+1}$
is continuous, being the composition of continuous maps
![]() $\mathcal {E}$
and
$\mathcal {E}$
and
![]() $\mathcal {H}_n$
. Hence, the continuity of
$\mathcal {H}_n$
. Hence, the continuity of
![]() $\mathcal {E}_n$
is proved for all
$\mathcal {E}_n$
is proved for all
![]() $n\in \mathbb {N}$
.
$n\in \mathbb {N}$
.
In fact, by putting
![]() $Y=X$
,
$Y=X$
,
![]() $Z=C(X)$
, and
$Z=C(X)$
, and
![]() $h=\mathcal {E}_n$
in Lemma 3, we get
$h=\mathcal {E}_n$
in Lemma 3, we get
![]() $F:C(X)\to C(X)$
and
$F:C(X)\to C(X)$
and
![]() $F(f)(x)=h(x,f)=\mathcal {E}_n(x,f)=\mathcal {J}_n(f)(x)$
for all
$F(f)(x)=h(x,f)=\mathcal {E}_n(x,f)=\mathcal {J}_n(f)(x)$
for all
![]() $f\in \mathcal {C}(X)$
and
$f\in \mathcal {C}(X)$
and
![]() $x\in X$
, implying that
$x\in X$
, implying that
![]() $F=\mathcal {J}_n$
. Thus, by Lemma 3, we see that
$F=\mathcal {J}_n$
. Thus, by Lemma 3, we see that
![]() $\mathcal {J}_n$
is continuous on
$\mathcal {J}_n$
is continuous on
![]() $\mathcal {C}(X)$
for each
$\mathcal {C}(X)$
for each
![]() $n\in \mathbb {N}$
.
$n\in \mathbb {N}$
.
Theorem 1 looks the same, but is more general than [Reference Veerapazham, Gopalakrishna and Zhang23, Theorem 2.1]. Unlike [Reference Veerapazham, Gopalakrishna and Zhang23], Theorem 1 does not assume X to be metrizable, which causes more difficulties in its proof. In the special case that X is a compact metric space with a metric d, the uniform topology induced by the metric
![]() $\rho $
gives the compact-open topology on
$\rho $
gives the compact-open topology on
![]() $\mathcal {C}(X)$
because of Lemma 1.
$\mathcal {C}(X)$
because of Lemma 1.
As indicated in §1,
![]() $\mathcal {J}_n$
defines a discrete semi-dynamical system on the space
$\mathcal {J}_n$
defines a discrete semi-dynamical system on the space
![]() $\mathcal {C}(X)$
of continuous functions with its iteration semigroup
$\mathcal {C}(X)$
of continuous functions with its iteration semigroup
![]() $\{\mathcal {J}_n^k: k\ge 0\}$
. Remark that
$\{\mathcal {J}_n^k: k\ge 0\}$
. Remark that
![]() $\mathcal {J}_n$
usually does not define a dynamical system because a homeomorphism f of a compact interval may have infinitely many iterative roots as indicated in [Reference Kuczma14].
$\mathcal {J}_n$
usually does not define a dynamical system because a homeomorphism f of a compact interval may have infinitely many iterative roots as indicated in [Reference Kuczma14].
3.1 Periodic points in general case
One of the most fundamental problems on dynamical systems or semi-dynamical systems concerns fixed points and periodic points. To emphasize the dependence on the space X, we use
![]() $\mathrm {Fix}(f;X)$
and
$\mathrm {Fix}(f;X)$
and
![]() $\mathrm {Per}(f;X)$
to denote the set of all fixed points and the set of all periodic points of f in X, respectively. Since
$\mathrm {Per}(f;X)$
to denote the set of all fixed points and the set of all periodic points of f in X, respectively. Since
![]() $ \mathcal {J}_n^k f=f^{n^k} $
by equation (1.1), we see that
$ \mathcal {J}_n^k f=f^{n^k} $
by equation (1.1), we see that
![]() $f\in \mathcal {C}(X)$
is a fixed point of
$f\in \mathcal {C}(X)$
is a fixed point of
![]() $\mathcal {J}_n$
if and only if f satisfies the functional equation
$\mathcal {J}_n$
if and only if f satisfies the functional equation
and
![]() $f\in \mathcal {C}(X)$
is a k-periodic point of
$f\in \mathcal {C}(X)$
is a k-periodic point of
![]() $\mathcal {J}_n$
if and only if f satisfies
$\mathcal {J}_n$
if and only if f satisfies
So, the fixed points and periodic points of
![]() $\mathcal {J}_n$
are related to solutions of the Babbage equation [Reference Kuczma14]
$\mathcal {J}_n$
are related to solutions of the Babbage equation [Reference Kuczma14]
where
![]() $m>0$
is a certain integer. The functional equations in equations (3.6) and (3.7) cannot be simply treated as the Babbage equation (3.8) because the range of f may not be the whole X. In what follows, we need to consider restriction of maps. For any
$m>0$
is a certain integer. The functional equations in equations (3.6) and (3.7) cannot be simply treated as the Babbage equation (3.8) because the range of f may not be the whole X. In what follows, we need to consider restriction of maps. For any
![]() $f\in \mathcal {C}(X)$
and
$f\in \mathcal {C}(X)$
and
![]() $A\subseteq X$
, let
$A\subseteq X$
, let
![]() $\bar {A}$
denote the closure of A,
$\bar {A}$
denote the closure of A,
![]() $R(f)$
the range of f, and
$R(f)$
the range of f, and
![]() $f|_A$
the restriction of f to A. As in [Reference Munkres21], a space X is said to be first countable if each point has a countable local basis, that is, for each
$f|_A$
the restriction of f to A. As in [Reference Munkres21], a space X is said to be first countable if each point has a countable local basis, that is, for each
![]() $x\in X$
, there exists a countable collection
$x\in X$
, there exists a countable collection
![]() $\mathcal {B}_x$
of neighborhoods of x such that each open set U containing x contains an element B of
$\mathcal {B}_x$
of neighborhoods of x such that each open set U containing x contains an element B of
![]() $\mathcal {B}_x$
.
$\mathcal {B}_x$
.
Lemma 5. Let
![]() $n\in \mathbb {N}$
and suppose that X is first countable. Then
$n\in \mathbb {N}$
and suppose that X is first countable. Then
![]() $f\in \mathcal {C}(X)$
is a solution of the equation
$f\in \mathcal {C}(X)$
is a solution of the equation
on X if and only if
![]() $R(f)$
is closed and there exists
$R(f)$
is closed and there exists
![]() $g\in \mathcal {C}(X)$
such that
$g\in \mathcal {C}(X)$
such that
![]() $R(g)=R(f)$
,
$R(g)=R(f)$
,
![]() $g|_{{R(g)}}$
satisfies the Babbage equation
$g|_{{R(g)}}$
satisfies the Babbage equation
on
![]() $R(g)$
, and
$R(g)$
, and
![]() $f|_{{R(g)}}=g|_{{R(f)}}$
.
$f|_{{R(g)}}=g|_{{R(f)}}$
.
Proof. If
![]() $f\in \mathcal {C}(X)$
is a solution of equation (3.9), then
$f\in \mathcal {C}(X)$
is a solution of equation (3.9), then
![]() $f^{n-1}(f(x))=f(x)$
for all
$f^{n-1}(f(x))=f(x)$
for all
![]() $x\in X$
, that is,
$x\in X$
, that is,
![]() $f^{n-1}(y)=y$
for all
$f^{n-1}(y)=y$
for all
![]() $y\in R(f)$
. Also, since X is first countable, for each
$y\in R(f)$
. Also, since X is first countable, for each
![]() $y\in \overline {R(f)}$
, there exists a sequence
$y\in \overline {R(f)}$
, there exists a sequence
![]() $(y_n)$
in
$(y_n)$
in
![]() $R(f)$
such that
$R(f)$
such that
![]() $y_k\to y$
, implying by continuity of f that
$y_k\to y$
, implying by continuity of f that
![]() $f(y_k)\to f(y)$
as
$f(y_k)\to f(y)$
as
![]() $k \to \infty $
. However,
$k \to \infty $
. However,
![]() $y_k=f^{n-1}(y_k)\to f^{n-1}(y)$
as
$y_k=f^{n-1}(y_k)\to f^{n-1}(y)$
as
![]() $k \to \infty $
. Therefore, as X is Hausdorff, we have
$k \to \infty $
. Therefore, as X is Hausdorff, we have
![]() $f(y)=y$
. Thus,
$f(y)=y$
. Thus,
![]() $y\in R(f)$
, and so
$y\in R(f)$
, and so
![]() $\overline {R(f)}=R(f)$
. Let
$\overline {R(f)}=R(f)$
. Let
![]() $g:=f$
. Then f is a continuous extension of the solution
$g:=f$
. Then f is a continuous extension of the solution
![]() $g|_{R(g)}$
on
$g|_{R(g)}$
on
![]() $R(g)$
to X such that
$R(g)$
to X such that
![]() $R(f)$
is closed,
$R(f)$
is closed,
![]() $R(g)= R(f)$
, and
$R(g)= R(f)$
, and
![]() $f|_{{R(g)}}=g|_{{R(f)}}$
. The proof of the converse is trivial, since for every
$f|_{{R(g)}}=g|_{{R(f)}}$
. The proof of the converse is trivial, since for every
![]() $g\in \mathcal {C}(X)$
, whose restriction
$g\in \mathcal {C}(X)$
, whose restriction
![]() $g|_{R(g)}$
satisfies
$g|_{R(g)}$
satisfies
![]() $\phi ^{n-1}=\mathrm {id}$
on
$\phi ^{n-1}=\mathrm {id}$
on
![]() $R(f)$
, we have
$R(f)$
, we have
![]() $f^n(x)=f^{n-1}(f(x))=g^{n-1}(f(x))=f(x)$
for all
$f^n(x)=f^{n-1}(f(x))=g^{n-1}(f(x))=f(x)$
for all
![]() $x\in X$
.
$x\in X$
.
Usually, a solution
![]() $\phi $
of equation (3.8) is referred to as an mth order unit iterative root if m is the smallest positive integer such that equation (3.8) is satisfied. Clearly, each unit iterative root is invertible. As in [Reference Kuczma14, p. 290], for
$\phi $
of equation (3.8) is referred to as an mth order unit iterative root if m is the smallest positive integer such that equation (3.8) is satisfied. Clearly, each unit iterative root is invertible. As in [Reference Kuczma14, p. 290], for
![]() $m=2$
, every solution of equation (3.8), whose inverse is itself, is called an involutory function. In general, if f is an mth order unit iterative root and
$m=2$
, every solution of equation (3.8), whose inverse is itself, is called an involutory function. In general, if f is an mth order unit iterative root and
![]() $f^k=\mathrm {id}$
, then m divides k clearly. On a general set E, the mth order unit iterative roots are formulated below.
$f^k=\mathrm {id}$
, then m divides k clearly. On a general set E, the mth order unit iterative roots are formulated below.
Lemma 6. [Reference Kuczma14, Theorem 15.1]
Let
![]() $\{m_0,\ldots ,m_r\}$
, where
$\{m_0,\ldots ,m_r\}$
, where
![]() $1=m_0<m_1<\cdots < m_r=m$
, be the complete set of divisors of m and let
$1=m_0<m_1<\cdots < m_r=m$
, be the complete set of divisors of m and let
![]() $E=\bigcup _{i=0}^{r}\bigcup _{j=1}^{m_i}U_j^i$
be a decomposition of E into disjoint sets such that the sets
$E=\bigcup _{i=0}^{r}\bigcup _{j=1}^{m_i}U_j^i$
be a decomposition of E into disjoint sets such that the sets
![]() $U_1^i, U_{m_1}^i,\ldots ,U_{m_i}^i$
have the same cardinality for each
$U_1^i, U_{m_1}^i,\ldots ,U_{m_i}^i$
have the same cardinality for each
![]() $1\le i \le r$
. For
$1\le i \le r$
. For
![]() $1\le i\le r$
and
$1\le i\le r$
and
![]() $1\le j \le m_i-1$
, let
$1\le j \le m_i-1$
, let
![]() $f_{ij}$
be an arbitrary one-to-one map of
$f_{ij}$
be an arbitrary one-to-one map of
![]() $U_j^i$
onto
$U_j^i$
onto
![]() $U_{j+1}^i$
. Then the formula
$U_{j+1}^i$
. Then the formula
 $$ \begin{align*} f(x):=\begin{cases} x&\text{for } x\in U_1^0,\\ f_{ij}(x)&\text{for } x\in U_j^i, j=1,2,\ldots,m_i-1, i\ge 1,\\ f_{i1}^{-1}(\cdots(f_{i,m_i-1}^{-1}(x))\cdots)&\text{for } x\in U_{m_i}^i, i\ge 1 \end{cases} \end{align*} $$
$$ \begin{align*} f(x):=\begin{cases} x&\text{for } x\in U_1^0,\\ f_{ij}(x)&\text{for } x\in U_j^i, j=1,2,\ldots,m_i-1, i\ge 1,\\ f_{i1}^{-1}(\cdots(f_{i,m_i-1}^{-1}(x))\cdots)&\text{for } x\in U_{m_i}^i, i\ge 1 \end{cases} \end{align*} $$
defines the general solution of
![]() $\phi ^m=\mathrm { id}$
on E.
$\phi ^m=\mathrm { id}$
on E.
Having Lemma 6, we are ready to define
for any subset E of X and
![]() $m\in \mathbb {N}$
. Since
$m\in \mathbb {N}$
. Since
![]() $\mathrm {Fix}(\mathcal {J}_1;X)=\mathcal {C}(X)$
, that is, the problem of fixed points of
$\mathrm {Fix}(\mathcal {J}_1;X)=\mathcal {C}(X)$
, that is, the problem of fixed points of
![]() $\mathcal {J}_1$
is trivial, we focus on
$\mathcal {J}_1$
is trivial, we focus on
![]() $\mathcal {J}_n$
with
$\mathcal {J}_n$
with
![]() $n\ge 2$
. We give the following results on fixed points and periodic points, whose proof is similar to that of [Reference Veerapazham, Gopalakrishna and Zhang23, Theorem 2.4].
$n\ge 2$
. We give the following results on fixed points and periodic points, whose proof is similar to that of [Reference Veerapazham, Gopalakrishna and Zhang23, Theorem 2.4].
Theorem 2. Let
![]() $n, k\ge 2$
be integers and suppose that X is first countable. Then: (i)
$n, k\ge 2$
be integers and suppose that X is first countable. Then: (i)
![]() $f\in \mathcal {C}(X)$
is a fixed point of
$f\in \mathcal {C}(X)$
is a fixed point of
![]() $\mathcal {J}_n$
if and only if
$\mathcal {J}_n$
if and only if
![]() $f\in \mathcal {U}_E^m$
for a closed subset E of X and an integer
$f\in \mathcal {U}_E^m$
for a closed subset E of X and an integer
![]() $m\ge 1$
dividing
$m\ge 1$
dividing
![]() $n-1$
exactly; (ii)
$n-1$
exactly; (ii)
![]() $f\in \mathcal {C}(X)$
is a k-periodic point of
$f\in \mathcal {C}(X)$
is a k-periodic point of
![]() $\mathcal {J}_n$
if and only if
$\mathcal {J}_n$
if and only if
![]() $f\in \mathcal {U}_E^m$
for a closed subset E of X and an integer
$f\in \mathcal {U}_E^m$
for a closed subset E of X and an integer
![]() $m>1$
satisfying that
$m>1$
satisfying that
Remark that we were able to infer that E is compact in [Reference Veerapazham, Gopalakrishna and Zhang23] because E is indeed
![]() $R(f)$
and domain X was assumed to be compact, but in Theorem 2, we can only conclude that E is closed because of using Lemma 5.
$R(f)$
and domain X was assumed to be compact, but in Theorem 2, we can only conclude that E is closed because of using Lemma 5.
Example 1. Consider
![]() $f(x)=|x|$
. Then
$f(x)=|x|$
. Then
![]() $f\in \mathcal {C}(\mathbb {R})$
. Clearly,
$f\in \mathcal {C}(\mathbb {R})$
. Clearly,
![]() $f\in \mathcal {U}_{[0,\infty )}^1$
. By result (i) of Theorem 2, f is a fixed point of
$f\in \mathcal {U}_{[0,\infty )}^1$
. By result (i) of Theorem 2, f is a fixed point of
![]() $\mathcal {J}_n$
for each
$\mathcal {J}_n$
for each
![]() $n\ge 2$
.
$n\ge 2$
.
Example 2. The doubling map
![]() $f\in \mathcal {C}(S^1)$
defined by
$f\in \mathcal {C}(S^1)$
defined by
![]() $f(e^{it})=e^{2it}$
is not a k-periodic point of
$f(e^{it})=e^{2it}$
is not a k-periodic point of
![]() $\mathcal {J}_n$
for
$\mathcal {J}_n$
for
![]() $n,k\ge 2$
. In fact, if
$n,k\ge 2$
. In fact, if
![]() $f^{n^k}=f$
for some
$f^{n^k}=f$
for some
![]() $n,k\ge 2$
, then
$n,k\ge 2$
, then
![]() $e^{it(2^{n^k}-2)}=0$
for all
$e^{it(2^{n^k}-2)}=0$
for all
![]() $t\in [0,2\pi )$
, which is a contradiction.
$t\in [0,2\pi )$
, which is a contradiction.
Example 3. The rotation map
![]() $R_{{2\pi }/({n^k-1})}:S^1\to S^1$
defined by
$R_{{2\pi }/({n^k-1})}:S^1\to S^1$
defined by
![]() $R_{{2\pi }/({n^k-1})}(e^{it})=e^{i(t+({2\pi }/({n^k-1})))}$
is a k-periodic point of
$R_{{2\pi }/({n^k-1})}(e^{it})=e^{i(t+({2\pi }/({n^k-1})))}$
is a k-periodic point of
![]() $\mathcal {J}_n$
in
$\mathcal {J}_n$
in
![]() $\mathcal {C}(S^1)$
for
$\mathcal {C}(S^1)$
for
![]() $n\ge 2$
and
$n\ge 2$
and
![]() $k\ge 1$
.
$k\ge 1$
.
3.2 Periodic points in
 $\mathcal {\mathcal {C}}(\mathbb {R})$
$\mathcal {\mathcal {C}}(\mathbb {R})$
For more detailed results, in this section, we focus on the case
![]() $X=\mathbb {R}$
, the real line in the usual topology. For
$X=\mathbb {R}$
, the real line in the usual topology. For
![]() $a,b \in \mathbb {R}$
with
$a,b \in \mathbb {R}$
with
![]() $a<b$
, let
$a<b$
, let
![]() $|a,b|$
denote either an open interval
$|a,b|$
denote either an open interval
![]() $(a,b)$
, a semi-closed interval
$(a,b)$
, a semi-closed interval
![]() $[a,b)$
or
$[a,b)$
or
![]() $(a,b]$
, or a closed interval
$(a,b]$
, or a closed interval
![]() $[a,b]$
, where one or both of the endpoints may be infinite. We have the following result, which can also be deduced from Lemma 6.
$[a,b]$
, where one or both of the endpoints may be infinite. We have the following result, which can also be deduced from Lemma 6.
Lemma 7. [Reference McShane18, Reference Vincze24]
If
![]() $f\in \mathcal {C}(|a,b|)$
is a solution of equation (3.8), then either
$f\in \mathcal {C}(|a,b|)$
is a solution of equation (3.8), then either
![]() $f=\mathrm {id}$
or f is a decreasing involutory function on
$f=\mathrm {id}$
or f is a decreasing involutory function on
![]() $|a,b|$
. More precisely, any solution of equation (3.8) on
$|a,b|$
. More precisely, any solution of equation (3.8) on
![]() $|a,b|$
for general m is also a second-order unit iterative root. If m is odd, then the solution is uniquely the identity
$|a,b|$
for general m is also a second-order unit iterative root. If m is odd, then the solution is uniquely the identity
![]() $\mathrm {id}$
; if m is even, then the solution is either id or a decreasing involutory function on
$\mathrm {id}$
; if m is even, then the solution is either id or a decreasing involutory function on
![]() $|a,b|$
.
$|a,b|$
.
In the following theorem, the proof of which is similar to that of [Reference Veerapazham, Gopalakrishna and Zhang23, Theorem 3.2] on a compact interval, we refer to monotonically increasing (or decreasing) functions satisfying equation (3.9) as monotonically increasing (or decreasing) fixed point of
![]() $\mathcal {J}_n$
.
$\mathcal {J}_n$
.
Theorem 3. Every monotonic fixed point f of
![]() $\mathcal {J}_2$
in
$\mathcal {J}_2$
in
![]() $\mathcal {C}(\mathbb {R})$
is of the first form in equation (3.11). Every monotonic fixed point f of
$\mathcal {C}(\mathbb {R})$
is of the first form in equation (3.11). Every monotonic fixed point f of
![]() $\mathcal {J}_3$
in
$\mathcal {J}_3$
in
![]() $\mathcal {C}(\mathbb {R})$
is of one of the following two forms:
$\mathcal {C}(\mathbb {R})$
is of one of the following two forms:
 $$ \begin{align} f(x)= \begin{cases} a & \text{if } x\in (-\infty,a|, \\ x & \text{if } x\in |a,b|, \\ b & \text{if } x\in |b, \infty), \end{cases} \ \ \ f(x)= \begin{cases} b & \text{if } x\in (-\infty,a|, \\ g(x) & \text{if } x\in |a,b|, \\ a & \text{if } x\in |b, \infty), \end{cases} \end{align} $$
$$ \begin{align} f(x)= \begin{cases} a & \text{if } x\in (-\infty,a|, \\ x & \text{if } x\in |a,b|, \\ b & \text{if } x\in |b, \infty), \end{cases} \ \ \ f(x)= \begin{cases} b & \text{if } x\in (-\infty,a|, \\ g(x) & \text{if } x\in |a,b|, \\ a & \text{if } x\in |b, \infty), \end{cases} \end{align} $$
where
![]() $|a,b|$
is a closed interval in
$|a,b|$
is a closed interval in
![]() $\mathbb {R}$
satisfying that
$\mathbb {R}$
satisfying that
![]() $a\le b$
and
$a\le b$
and
![]() $g\in \mathcal {C}(|a,b|)$
is a decreasing involutory map.
$g\in \mathcal {C}(|a,b|)$
is a decreasing involutory map.
The above theorem is only applicable to monotonic fixed points. There exist fixed points of
![]() $\mathcal {J}_2$
or
$\mathcal {J}_2$
or
![]() $\mathcal {J}_3$
which are not monotonic. For example, as considered in Example 1, the function
$\mathcal {J}_3$
which are not monotonic. For example, as considered in Example 1, the function
![]() $f(x)=|x|$
on
$f(x)=|x|$
on
![]() $\mathbb {R}$
is not a monotonic map on
$\mathbb {R}$
is not a monotonic map on
![]() $\mathbb {R}$
but a fixed point of
$\mathbb {R}$
but a fixed point of
![]() $\mathcal {J}_2$
.
$\mathcal {J}_2$
.
The ‘monotone’ in Theorem 3 need not mean ‘strict monotone’. In fact, if
![]() $a\in \mathbb {R}$
in the first form of equation (3.11), then we have
$a\in \mathbb {R}$
in the first form of equation (3.11), then we have
![]() $f(x)=a$
for
$f(x)=a$
for
![]() $x\in (-\infty , a]$
, implying that f is not strictly monotone. For strictly monotonic ones, we have the following result, the proof of which is similar to that of [Reference Veerapazham, Gopalakrishna and Zhang23, Corollary 3.3] on a compact interval.
$x\in (-\infty , a]$
, implying that f is not strictly monotone. For strictly monotonic ones, we have the following result, the proof of which is similar to that of [Reference Veerapazham, Gopalakrishna and Zhang23, Corollary 3.3] on a compact interval.
Corollary 1. If f is a strictly monotonic fixed point of
![]() $\mathcal {J}_3$
in
$\mathcal {J}_3$
in
![]() $\mathcal {C}(\mathbb {R})$
, then either
$\mathcal {C}(\mathbb {R})$
, then either
![]() $f=\mathrm {id}$
or f is a strictly decreasing involutory function on
$f=\mathrm {id}$
or f is a strictly decreasing involutory function on
![]() $\mathbb {R}$
.
$\mathbb {R}$
.
Theorem 3 gives results only for
![]() $\mathcal {J}_2$
and
$\mathcal {J}_2$
and
![]() $\mathcal {J}_3$
, but not for the generic
$\mathcal {J}_3$
, but not for the generic
![]() $\mathcal {J}_n$
. In what follows, we show that those monotonic fixed points of
$\mathcal {J}_n$
. In what follows, we show that those monotonic fixed points of
![]() $\mathcal {J}_2$
and
$\mathcal {J}_2$
and
![]() $\mathcal {J}_3$
are important representatives for the generic
$\mathcal {J}_3$
are important representatives for the generic
![]() $\mathcal {J}_n$
. Let
$\mathcal {J}_n$
. Let
![]() $\mathcal {C}_{\mathrm {id}}(\mathbb {R})$
and
$\mathcal {C}_{\mathrm {id}}(\mathbb {R})$
and
![]() $\mathcal {C}_{\mathrm {inv}}(\mathbb {R})$
consist of all continuous self-maps of
$\mathcal {C}_{\mathrm {inv}}(\mathbb {R})$
consist of all continuous self-maps of
![]() $\mathbb {R}$
which are the identity and decreasing involutions on their range, respectively. By Theorem 3, monotonic fixed points of
$\mathbb {R}$
which are the identity and decreasing involutions on their range, respectively. By Theorem 3, monotonic fixed points of
![]() $\mathcal {J}_3$
are in both classes
$\mathcal {J}_3$
are in both classes
![]() $\mathcal {C}_{\mathrm {id}}(\mathbb {R})$
and
$\mathcal {C}_{\mathrm {id}}(\mathbb {R})$
and
![]() $\mathcal {C}_{\mathrm {inv}}(\mathbb {R})$
but monotonic fixed points of
$\mathcal {C}_{\mathrm {inv}}(\mathbb {R})$
but monotonic fixed points of
![]() $\mathcal {J}_2$
are all in the same class
$\mathcal {J}_2$
are all in the same class
![]() $\mathcal {C}_{\mathrm {id}}(\mathbb {R})$
. The following theorem, the proof of which is similar to that of [Reference Veerapazham, Gopalakrishna and Zhang23, Theorem 3.4] on a compact interval, describes all fixed points of
$\mathcal {C}_{\mathrm {id}}(\mathbb {R})$
. The following theorem, the proof of which is similar to that of [Reference Veerapazham, Gopalakrishna and Zhang23, Theorem 3.4] on a compact interval, describes all fixed points of
![]() $\mathcal {J}_n$
for any
$\mathcal {J}_n$
for any
![]() $n\ge 2$
.
$n\ge 2$
.
Theorem 4. The following statements are true for system
![]() $(\mathcal {C}(\mathbb {R}), \mathcal {J}_n)$
:
$(\mathcal {C}(\mathbb {R}), \mathcal {J}_n)$
:
-
(i)
 $\mathrm {Fix}(\mathcal {J}_m;\mathcal {C}(\mathbb {R}))=\mathrm {Fix}(\mathcal {J}_n;\mathcal {C}(\mathbb {R}))$
if integers
$\mathrm {Fix}(\mathcal {J}_m;\mathcal {C}(\mathbb {R}))=\mathrm {Fix}(\mathcal {J}_n;\mathcal {C}(\mathbb {R}))$
if integers
 $m,n\ge 2$
satisfy
$m,n\ge 2$
satisfy
 $m\equiv n(\mathrm {mod} ~2)$
;
$m\equiv n(\mathrm {mod} ~2)$
; -
(ii)
 $\mathrm {Fix}(\mathcal {J}_2;\mathcal {C}(\mathbb {R}))\subsetneq \mathrm {Fix}(\mathcal {J}_3;\mathcal {C}(\mathbb {R}))$
. More concretely,
$\mathrm {Fix}(\mathcal {J}_2;\mathcal {C}(\mathbb {R}))\subsetneq \mathrm {Fix}(\mathcal {J}_3;\mathcal {C}(\mathbb {R}))$
. More concretely, $\mathrm {Fix}(\mathcal {J}_2;\mathcal {C}(\mathbb {R}))=\mathcal {C}_{\mathrm {id}}(\mathbb {R})$
and
$\mathrm {Fix}(\mathcal {J}_2;\mathcal {C}(\mathbb {R}))=\mathcal {C}_{\mathrm {id}}(\mathbb {R})$
and
 $\mathrm {Fix}(\mathcal {J}_3;\mathcal {C}(\mathbb {R}))=\mathcal {C}_{\mathrm {id}}(\mathbb {R})\cup \mathcal {C}_{\mathrm {inv}}(\mathbb {R})$
.
$\mathrm {Fix}(\mathcal {J}_3;\mathcal {C}(\mathbb {R}))=\mathcal {C}_{\mathrm {id}}(\mathbb {R})\cup \mathcal {C}_{\mathrm {inv}}(\mathbb {R})$
.
Theorem 3 together with result (i) of Theorem 4 shows that Theorem 3 is indeed true for every integer
![]() $n\ge 2$
. More precisely, monotonic fixed points of
$n\ge 2$
. More precisely, monotonic fixed points of
![]() $\mathcal {J}_n$
coincide with those of
$\mathcal {J}_n$
coincide with those of
![]() $\mathcal {J}_2$
and
$\mathcal {J}_2$
and
![]() $\mathcal {J}_3$
accordingly as n is even and odd, respectively. So, Theorem 3 actually gives results for the representatives.
$\mathcal {J}_3$
accordingly as n is even and odd, respectively. So, Theorem 3 actually gives results for the representatives.
Although we can find many fixed points of
![]() ${\cal J}_n$
, there are no non-trivial periodic points as seen from the following result, the proof of which is similar to that of [Reference Veerapazham, Gopalakrishna and Zhang23, Theorem 3.5] on a compact interval.
${\cal J}_n$
, there are no non-trivial periodic points as seen from the following result, the proof of which is similar to that of [Reference Veerapazham, Gopalakrishna and Zhang23, Theorem 3.5] on a compact interval.
Theorem 5. For each
![]() $n\in \mathbb {N}, ~{\cal J}_n$
does not have periodic points of period
$n\in \mathbb {N}, ~{\cal J}_n$
does not have periodic points of period
![]() $k\ge 2$
in
$k\ge 2$
in
![]() $\mathcal {C}(\mathbb {R})$
.
$\mathcal {C}(\mathbb {R})$
.
As observed earlier, every element of
![]() $\mathcal {C}(\mathbb {R})$
is a fixed point for
$\mathcal {C}(\mathbb {R})$
is a fixed point for
![]() $\mathcal {J}_1$
. So,
$\mathcal {J}_1$
. So,
![]() $\mathcal {J}_1$
has a dense set of periodic points in
$\mathcal {J}_1$
has a dense set of periodic points in
![]() $\mathcal {C}(\mathbb {R})$
. However, since
$\mathcal {C}(\mathbb {R})$
. However, since
![]() $\mathcal {C}(\mathbb {R})$
is metrizable with metric D by result (i) of Lemma 4 and
$\mathcal {C}(\mathbb {R})$
is metrizable with metric D by result (i) of Lemma 4 and
![]() $\mathcal {J}_n$
is not the identity operator on
$\mathcal {J}_n$
is not the identity operator on
![]() $\mathcal {C}(\mathbb {R})$
, it follows that
$\mathcal {C}(\mathbb {R})$
, it follows that
![]() $\mathrm {Fix}(\mathcal {J}_n;\mathcal {C}(\mathbb {R}))$
is not dense in
$\mathrm {Fix}(\mathcal {J}_n;\mathcal {C}(\mathbb {R}))$
is not dense in
![]() $\mathcal {C}(\mathbb {R})$
for
$\mathcal {C}(\mathbb {R})$
for
![]() $n\ge 2$
. This implies by Theorem 5 that
$n\ge 2$
. This implies by Theorem 5 that
![]() $\mathrm {Per}(\mathcal {J}_n;\mathcal {C}(\mathbb {R}))$
is not dense in
$\mathrm {Per}(\mathcal {J}_n;\mathcal {C}(\mathbb {R}))$
is not dense in
![]() $\mathcal {C}(\mathbb {R})$
for
$\mathcal {C}(\mathbb {R})$
for
![]() $n\ge 2$
.
$n\ge 2$
.
3.3 Periodic points in
 $\mathcal {\mathcal {C}}(S^1)$
$\mathcal {\mathcal {C}}(S^1)$
As illustrated in Example 3,
![]() ${\cal J}_n$
may have periodic points of period
${\cal J}_n$
may have periodic points of period
![]() $k\ge 2$
in
$k\ge 2$
in
![]() $\mathcal {C}(S^1)$
but, in contrast,
$\mathcal {C}(S^1)$
but, in contrast,
![]() ${\cal J}_n$
only has fixed points, that is, trivial periodic points of period 1, in
${\cal J}_n$
only has fixed points, that is, trivial periodic points of period 1, in
![]() $\mathcal {C}(\mathbb {R})$
as shown in Theorem 5. In this section, we investigate all periodic points of
$\mathcal {C}(\mathbb {R})$
as shown in Theorem 5. In this section, we investigate all periodic points of
![]() $\mathcal {J}_n$
in
$\mathcal {J}_n$
in
![]() $\mathcal {C}(S^1)$
.
$\mathcal {C}(S^1)$
.
Given
![]() $z_0, z_1, \ldots , z_{m-1}\in S^1$
with
$z_0, z_1, \ldots , z_{m-1}\in S^1$
with
![]() $m\ge 2$
, we write
$m\ge 2$
, we write
![]() $ z_0\prec z_1\prec \cdots \prec z_{m-1} $
if there exist
$ z_0\prec z_1\prec \cdots \prec z_{m-1} $
if there exist
![]() $t_1,t_2,\ldots ,t_{m-1}\in \mathbb {R}$
such that
$t_1,t_2,\ldots ,t_{m-1}\in \mathbb {R}$
such that
![]() $0<t_1<t_2<\cdots <t_{m-1}<1 ~\text {and}~ z_j=z_0e^{2\pi i t_j}~\text {for}~1\le j \le m-1. $
In this case, we have
$0<t_1<t_2<\cdots <t_{m-1}<1 ~\text {and}~ z_j=z_0e^{2\pi i t_j}~\text {for}~1\le j \le m-1. $
In this case, we have
so that ‘
![]() $\prec $
’ is indeed a cyclic order on
$\prec $
’ is indeed a cyclic order on
![]() $S^1$
.
$S^1$
.
For any two distinct points
![]() $z_1, z_2\in S^1$
, define the arcs
$z_1, z_2\in S^1$
, define the arcs
![]() $(z_1, z_2)$
,
$(z_1, z_2)$
,
![]() $[z_1, z_2)$
, and
$[z_1, z_2)$
, and
![]() $(z_1, z_2]$
by
$(z_1, z_2]$
by
![]() $(z_1,z_2):=\{z\in S^1:z_1\prec z\prec z_2\},$
$(z_1,z_2):=\{z\in S^1:z_1\prec z\prec z_2\},$
![]() $[z_1, z_2):=(z_1, z_2)\cup \{z_1\},~ \text {and}~(z_1, z_2]:=(z_1, z_2)\cup \{z_2\}.$
Then we have
$[z_1, z_2):=(z_1, z_2)\cup \{z_1\},~ \text {and}~(z_1, z_2]:=(z_1, z_2)\cup \{z_2\}.$
Then we have
![]() $ (z_1,z_2)=\{e^{2\pi it}\in S^1:t\in (t_1, t_2)\},$
where
$ (z_1,z_2)=\{e^{2\pi it}\in S^1:t\in (t_1, t_2)\},$
where
![]() $t_1, t_2$
are unique real such that
$t_1, t_2$
are unique real such that
![]() $z_1=e^{2\pi it_1}, z_2=e^{2\pi it_2}$
, and
$z_1=e^{2\pi it_1}, z_2=e^{2\pi it_2}$
, and
![]() $0\le t_1<t_2<t_1+1<2$
.
$0\le t_1<t_2<t_1+1<2$
.
It is known (cf. [Reference Block and Coppel4, Reference Wall25]) that for every homeomorphism
![]() $F:S^1\to S^1$
, there exists a homeomorphism
$F:S^1\to S^1$
, there exists a homeomorphism
![]() $f:\mathbb {R}\to \mathbb {R}$
satisfying one of the Abel equations:
$f:\mathbb {R}\to \mathbb {R}$
satisfying one of the Abel equations:
 $$ \begin{align*} &f(t+1)=f(t)+1 \quad\text{if }f\text{ is strictly increasing;} \\ &f(t+1)=f(t)-1 \quad\text{if }f\text{ is strictly decreasing} \end{align*} $$
$$ \begin{align*} &f(t+1)=f(t)+1 \quad\text{if }f\text{ is strictly increasing;} \\ &f(t+1)=f(t)-1 \quad\text{if }f\text{ is strictly decreasing} \end{align*} $$
such that
![]() $ F(e^{2\pi it})=e^{2\pi if(t)} \ \text { for all } t\in \mathbb {R}. $
Every such f is called a lift of F. We say that F preserves (or reverses) orientation accordingly as f is strictly increasing (or decreasing) on
$ F(e^{2\pi it})=e^{2\pi if(t)} \ \text { for all } t\in \mathbb {R}. $
Every such f is called a lift of F. We say that F preserves (or reverses) orientation accordingly as f is strictly increasing (or decreasing) on
![]() $\mathbb {R}$
.
$\mathbb {R}$
.
The following two lemmas together describe the general solution of equation (3.8) on
![]() $S^1$
, each of which can also be deduced from Lemma 6.
$S^1$
, each of which can also be deduced from Lemma 6.
Lemma 8. [Reference Jarczyk12]
Let
![]() $\phi \in \mathcal {C}(S^1)$
be a solution of equation (3.8) and have a fixed point in
$\phi \in \mathcal {C}(S^1)$
be a solution of equation (3.8) and have a fixed point in
![]() $S^1$
. Then: (i)
$S^1$
. Then: (i)
![]() $\phi $
is the identity map if
$\phi $
is the identity map if
![]() $\phi $
is orientation-preserving; or (ii)
$\phi $
is orientation-preserving; or (ii)
![]() $\phi $
is an involution if
$\phi $
is an involution if
![]() $\phi $
is orientation-reversing.
$\phi $
is orientation-reversing.
Lemma 9. [Reference Jarczyk12]
All mth-order iterative roots of identity in
![]() $\mathcal {C}(S^1)$
having no fixed points in
$\mathcal {C}(S^1)$
having no fixed points in
![]() $S^1$
are given by
$S^1$
are given by
 $$ \begin{align} f(z)=\begin{cases} \phi_0(z)&\text{if } z\in [z_0,z_{m-1}),\\ (\phi_1\circ \phi_2\circ \cdots \circ \phi_{m-1})^{-1}(z)& \text{if } z\in [z_{m-1},z_0) \end{cases} \end{align} $$
$$ \begin{align} f(z)=\begin{cases} \phi_0(z)&\text{if } z\in [z_0,z_{m-1}),\\ (\phi_1\circ \phi_2\circ \cdots \circ \phi_{m-1})^{-1}(z)& \text{if } z\in [z_{m-1},z_0) \end{cases} \end{align} $$
with
![]() $\phi _j:=\phi _0|_{[z_{j(m-k)-1}, z_{j(m-k)})}~\text {for}~1\le j \le m-1$
, where k is an integer in
$\phi _j:=\phi _0|_{[z_{j(m-k)-1}, z_{j(m-k)})}~\text {for}~1\le j \le m-1$
, where k is an integer in
![]() $\{1,2,\ldots , m-1\}$
relatively prime to m and
$\{1,2,\ldots , m-1\}$
relatively prime to m and
![]() $z_0, z_1, \ldots , z_{m-1}$
are some points in
$z_0, z_1, \ldots , z_{m-1}$
are some points in
![]() $S^1$
such that
$S^1$
such that
![]() $z_0\prec z_1\prec \cdots \prec z_{m-1}$
, and
$z_0\prec z_1\prec \cdots \prec z_{m-1}$
, and
![]() $\phi _0:[z_0, z_{m-1}) \to [z_k,z_{k-1})$
is any arbitrary homeomorphism such that
$\phi _0:[z_0, z_{m-1}) \to [z_k,z_{k-1})$
is any arbitrary homeomorphism such that
![]() $ \phi _0([z_{j-1},z_j))=[z_{j-1+k},z_{j+k})~\text {for}~ 1\le j\le m-1 $
with
$ \phi _0([z_{j-1},z_j))=[z_{j-1+k},z_{j+k})~\text {for}~ 1\le j\le m-1 $
with
![]() $z_j:=z_{j(\mathrm {mod~m})}$
for
$z_j:=z_{j(\mathrm {mod~m})}$
for
![]() $j\ge m$
.
$j\ge m$
.
The following two theorems characterize fixed points and periodic points of
![]() $\mathcal {J}_n$
in
$\mathcal {J}_n$
in
![]() $\mathcal {C}(S^1)$
.
$\mathcal {C}(S^1)$
.
Theorem 6. Let
![]() $n\in \mathbb {N}$
. Then
$n\in \mathbb {N}$
. Then
![]() $f\in \mathcal {C}(S^1)$
is a fixed point of
$f\in \mathcal {C}(S^1)$
is a fixed point of
![]() $\mathcal {J}_n$
if and only if one of the following conditions is satisfied: (i)
$\mathcal {J}_n$
if and only if one of the following conditions is satisfied: (i)
![]() $f|_{R(f)}$
is the identity map; (ii)
$f|_{R(f)}$
is the identity map; (ii)
![]() $f|_{R(f)}$
is an orientation-reversing involution; or (iii) f is of the form equation (3.12) for a divisor m of
$f|_{R(f)}$
is an orientation-reversing involution; or (iii) f is of the form equation (3.12) for a divisor m of
![]() $n-1$
.
$n-1$
.
Proof. Let
![]() $n\in \mathbb {N}$
. To find all fixed points of
$n\in \mathbb {N}$
. To find all fixed points of
![]() $\mathcal {J}_n$
in
$\mathcal {J}_n$
in
![]() $\mathcal {C}(S^1)$
, in view of Lemma 5, it suffices to find all
$\mathcal {C}(S^1)$
, in view of Lemma 5, it suffices to find all
![]() $f\in \mathcal {C}(S^1)$
satisfying the equation
$f\in \mathcal {C}(S^1)$
satisfying the equation
![]() $\phi ^{n-1}=\text {id}$
on
$\phi ^{n-1}=\text {id}$
on
![]() $R(f)$
. So let
$R(f)$
. So let
![]() $f\in \mathcal {C}(S^1)$
be such that
$f\in \mathcal {C}(S^1)$
be such that
![]() $f^{n-1}=\text {id}$
on
$f^{n-1}=\text {id}$
on
![]() $R(f)$
. Since
$R(f)$
. Since
![]() $S^1$
is connected and compact,
$S^1$
is connected and compact,
![]() $R(f)$
is either a singleton set, an arc, or the whole of
$R(f)$
is either a singleton set, an arc, or the whole of
![]() $S^1$
.
$S^1$
.
Suppose
![]() $R(f)=S^1$
. If f has a fixed point, then by Lemma 8, f is either the identity map or an involution according as f is orientation-preserving or orientation-reversing. If f has no fixed points, then by Lemma 9, f is of the form in equation (3.12) for some divisor m of
$R(f)=S^1$
. If f has a fixed point, then by Lemma 8, f is either the identity map or an involution according as f is orientation-preserving or orientation-reversing. If f has no fixed points, then by Lemma 9, f is of the form in equation (3.12) for some divisor m of
![]() $n-1$
.
$n-1$
.
Now suppose that
![]() $R(f)\subsetneq S^1$
. Then
$R(f)\subsetneq S^1$
. Then
![]() $R(f)$
is either a singleton set or an arc in
$R(f)$
is either a singleton set or an arc in
![]() $S^1$
. If
$S^1$
. If
![]() $R(f)$
is a singleton set, then f is a constant map on
$R(f)$
is a singleton set, then f is a constant map on
![]() $S^1$
. If
$S^1$
. If
![]() $R(f)$
is an arc, say
$R(f)$
is an arc, say
![]() $[z_1,z_2]$
for some
$[z_1,z_2]$
for some
![]() $z_1, z_2 \in S^1$
, then consider a homeomorphism
$z_1, z_2 \in S^1$
, then consider a homeomorphism
![]() $h_f:R(f)\to [t_1, t_2]$
, where
$h_f:R(f)\to [t_1, t_2]$
, where
![]() $t_1, t_2$
are unique reals satisfying the conditions
$t_1, t_2$
are unique reals satisfying the conditions
![]() $z_1{\kern-1pt}={\kern-1pt}e^{2\pi it_1}, z_2{\kern-1pt}={\kern-1pt}e^{2\pi it_2}$
and
$z_1{\kern-1pt}={\kern-1pt}e^{2\pi it_1}, z_2{\kern-1pt}={\kern-1pt}e^{2\pi it_2}$
and
![]() $0{\kern-1pt}\le{\kern-1pt} t_1{\kern-1pt}<{\kern-1pt}t_2{\kern-1pt}<{\kern-1pt}t_1{\kern-1pt}+{\kern-1pt}1<2$
. Define a map
$0{\kern-1pt}\le{\kern-1pt} t_1{\kern-1pt}<{\kern-1pt}t_2{\kern-1pt}<{\kern-1pt}t_1{\kern-1pt}+{\kern-1pt}1<2$
. Define a map
![]() $\mathcal {H}_f:\mathcal {C}(R(f)) \to \mathcal {C}([t_1, t_2])$
by
$\mathcal {H}_f:\mathcal {C}(R(f)) \to \mathcal {C}([t_1, t_2])$
by
Then
![]() $\mathcal {H}_f$
is a bijective, bi-continuous map such that
$\mathcal {H}_f$
is a bijective, bi-continuous map such that
![]() $\mathcal {H}_f\circ \mathcal {J}_n=\mathcal {J}_n\circ \mathcal {H}_f$
(that is,
$\mathcal {H}_f\circ \mathcal {J}_n=\mathcal {J}_n\circ \mathcal {H}_f$
(that is,
![]() $(\mathcal {C}(R(f)), \mathcal {J}_n)$
is topologically conjugate to
$(\mathcal {C}(R(f)), \mathcal {J}_n)$
is topologically conjugate to
![]() $(\mathcal {C}([t_1, t_2]), \mathcal {J}_n)$
). Now since
$(\mathcal {C}([t_1, t_2]), \mathcal {J}_n)$
). Now since
![]() $f^{n-1}=\text {id}$
on
$f^{n-1}=\text {id}$
on
![]() $R(f)$
, we have
$R(f)$
, we have
![]() $\mathcal {H}_f(f^{n-1})=\mathcal {H}_f(\text {id})=\text {id} $
on
$\mathcal {H}_f(f^{n-1})=\mathcal {H}_f(\text {id})=\text {id} $
on
![]() $[t_1, t_2]$
, that is,
$[t_1, t_2]$
, that is,
![]() $(h_f\circ f\circ h_f^{-1})^{n-1}=\text {id}$
on
$(h_f\circ f\circ h_f^{-1})^{n-1}=\text {id}$
on
![]() $[t_1, t_2]$
. Therefore, by Lemma 7,
$[t_1, t_2]$
. Therefore, by Lemma 7,
![]() $h_f\circ f\circ h_f^{-1}$
is either the identity map or a decreasing involutory map on
$h_f\circ f\circ h_f^{-1}$
is either the identity map or a decreasing involutory map on
![]() $[t_1, t_2]$
. This implies that
$[t_1, t_2]$
. This implies that
![]() $f|_{R(f)}$
is either an identity map or an orientation-reversing involutory map.
$f|_{R(f)}$
is either an identity map or an orientation-reversing involutory map.
Conversely, if
![]() $f\in \mathcal {C}(S^1)$
satisfies either of the conditions (i) or (ii), then
$f\in \mathcal {C}(S^1)$
satisfies either of the conditions (i) or (ii), then
![]() $f^n=f$
on
$f^n=f$
on
![]() $S^1$
implying that f is a fixed point of
$S^1$
implying that f is a fixed point of
![]() $\mathcal {J}_n$
. If f satisfies condition (iii), then by Lemma 9, we have
$\mathcal {J}_n$
. If f satisfies condition (iii), then by Lemma 9, we have
![]() $f^m=\mathrm {id}$
on
$f^m=\mathrm {id}$
on
![]() $S^1$
, and therefore
$S^1$
, and therefore
![]() $f^{n-1}=\mathrm {id}$
on
$f^{n-1}=\mathrm {id}$
on
![]() $S^1$
as m divides
$S^1$
as m divides
![]() $n-1$
. Therefore, f is a fixed point of
$n-1$
. Therefore, f is a fixed point of
![]() $\mathcal {J}_n$
.
$\mathcal {J}_n$
.
Theorem 7. Let
![]() $n, k\ge 2$
. Then
$n, k\ge 2$
. Then
![]() $f\in \mathcal {C}(S^1)$
is a k-periodic point of
$f\in \mathcal {C}(S^1)$
is a k-periodic point of
![]() $\mathcal {J}_n$
if and only if f is of the form in equation (3.12) for some
$\mathcal {J}_n$
if and only if f is of the form in equation (3.12) for some
![]() $m>1$
such that
$m>1$
such that
![]() $m\mid (n^k-1)$
and
$m\mid (n^k-1)$
and
![]() $m\nmid (n^j-1)$
for
$m\nmid (n^j-1)$
for
![]() $1\le j\le k-1$
.
$1\le j\le k-1$
.
Proof. Let
![]() $f\in \mathcal {C}(S^1)$
be a k-periodic point of
$f\in \mathcal {C}(S^1)$
be a k-periodic point of
![]() $\mathcal {J}_n$
. Then f satisfies
$\mathcal {J}_n$
. Then f satisfies
on
![]() $S^1$
and also by result (ii) of Theorem 2,
$S^1$
and also by result (ii) of Theorem 2,
![]() $f\in \mathcal {U}_E^m$
for some compact subset E of K and
$f\in \mathcal {U}_E^m$
for some compact subset E of K and
![]() $m>1$
satisfying equation (3.10). In fact, here
$m>1$
satisfying equation (3.10). In fact, here
![]() $E=R(f)$
. We assert that
$E=R(f)$
. We assert that
![]() $E=S^1$
. Note that E, being the image of connected and compact set
$E=S^1$
. Note that E, being the image of connected and compact set
![]() $S^1$
under f, is either a singleton set, an arc, or
$S^1$
under f, is either a singleton set, an arc, or
![]() $S^1$
. If E is a singleton, then f is a constant map on
$S^1$
. If E is a singleton, then f is a constant map on
![]() $S^1$
, and therefore
$S^1$
, and therefore
![]() $f^n=f$
, which is a contradiction to equation (3.13). If E is an arc, then
$f^n=f$
, which is a contradiction to equation (3.13). If E is an arc, then
![]() $f|_E$
is either the identity map or an orientation-reversing involution. In any case, we arrive at a contradiction to equation (3.13). Therefore,
$f|_E$
is either the identity map or an orientation-reversing involution. In any case, we arrive at a contradiction to equation (3.13). Therefore,
![]() $E=S^1$
so that
$E=S^1$
so that
![]() $f\in \mathcal {U}_{S^1}^m$
. This implies by Lemma 9 that f is of the form in equation (3.12).
$f\in \mathcal {U}_{S^1}^m$
. This implies by Lemma 9 that f is of the form in equation (3.12).
Conversely, if f is of the form in equation (3.12) for some
![]() $m>1$
such that
$m>1$
such that
![]() $m\mid (n^k-1)$
and
$m\mid (n^k-1)$
and
![]() $m\nmid (n^j-1)$
for
$m\nmid (n^j-1)$
for
![]() $1\le j\le k-1$
, then clearly
$1\le j\le k-1$
, then clearly
![]() $f\in \mathcal {U}_{S^1}^m$
with
$f\in \mathcal {U}_{S^1}^m$
with
![]() $m>1$
satisfying equation (3.10) so that by result (ii) of Theorem 2, f is a k-periodic point of
$m>1$
satisfying equation (3.10) so that by result (ii) of Theorem 2, f is a k-periodic point of
![]() $\mathcal {J}_n$
.
$\mathcal {J}_n$
.
4 Stability in
 $\mathcal {J}_n$
$\mathcal {J}_n$
In this section, we study the (Lyapunov) stability of fixed points of the iteration operator
![]() $\mathcal {J}_n$
. In view of Lemma 4, to investigate boundedness of orbits, in the following, we consider X to be a hemicompact metrizable space. Clearly, all the orbits of
$\mathcal {J}_n$
. In view of Lemma 4, to investigate boundedness of orbits, in the following, we consider X to be a hemicompact metrizable space. Clearly, all the orbits of
![]() $\mathcal {J}_n$
are bounded because
$\mathcal {J}_n$
are bounded because
![]() $D(f,g)=\sum _{j=1}^{\infty }\mu _j(f,g)\le \sum _{j=1}^{\infty }{1}/{2^j}=1$
for all
$D(f,g)=\sum _{j=1}^{\infty }\mu _j(f,g)\le \sum _{j=1}^{\infty }{1}/{2^j}=1$
for all
![]() $f, g\in \mathcal {C}(X).$
In particular, when X is a compact metric space with metric d, we can let
$f, g\in \mathcal {C}(X).$
In particular, when X is a compact metric space with metric d, we can let
![]() $X=\bigcup _{j=1}^{\infty }K_j$
such that
$X=\bigcup _{j=1}^{\infty }K_j$
such that
![]() $K_1=X$
and
$K_1=X$
and
![]() $K_j=\emptyset $
for all
$K_j=\emptyset $
for all
![]() $j\ge 2$
, implying that the metric D of
$j\ge 2$
, implying that the metric D of
![]() $\mathcal {C}(X)$
is
$\mathcal {C}(X)$
is
![]() $D(f,g)=\mu (f,g)=\min \{\tfrac 12, \rho (f,g)\}$
, which is also equivalent to the uniform metric
$D(f,g)=\mu (f,g)=\min \{\tfrac 12, \rho (f,g)\}$
, which is also equivalent to the uniform metric
![]() $\rho $
on it. Further, the boundedness of orbits of
$\rho $
on it. Further, the boundedness of orbits of
![]() $\mathcal {J}_n$
in
$\mathcal {J}_n$
in
![]() $\mathcal {C}(X)$
can also be proved as follows. Since X is compact, there exist
$\mathcal {C}(X)$
can also be proved as follows. Since X is compact, there exist
![]() $y\in X$
and
$y\in X$
and
![]() $M>0$
such that
$M>0$
such that
![]() $d(x,y)\le {M}/{2}$
, implying that
$d(x,y)\le {M}/{2}$
, implying that
![]() $d(f^{n^k}(x), f^{n^l}(x)) \le d(f^{n^k}(x), y)+d(y, f^{n^l}(x)) \le M$
for all
$d(f^{n^k}(x), f^{n^l}(x)) \le d(f^{n^k}(x), y)+d(y, f^{n^l}(x)) \le M$
for all
![]() $x \in X$
and
$x \in X$
and
![]() $k, l \in \mathbb {N}$
. So, we can work with metric
$k, l \in \mathbb {N}$
. So, we can work with metric
![]() $\rho $
of
$\rho $
of
![]() $\mathcal {C}(X)$
instead of D whenever X is compact.
$\mathcal {C}(X)$
instead of D whenever X is compact.
As defined in [Reference Milnor19], the orbit
![]() $(f^n(x))_{n\in \mathbb {N}\cup \{0\}}$
of a discrete semi-dynamical system
$(f^n(x))_{n\in \mathbb {N}\cup \{0\}}$
of a discrete semi-dynamical system
![]() $(X,f)$
, where X is a metric space equipped with the metric d, is said to be (Lyapunov) stable if for every
$(X,f)$
, where X is a metric space equipped with the metric d, is said to be (Lyapunov) stable if for every
![]() $\epsilon>0$
, there exists
$\epsilon>0$
, there exists
![]() $\delta>0$
such that
$\delta>0$
such that
![]() $ d(f^k(x),f^k(y))<\epsilon $
for all
$ d(f^k(x),f^k(y))<\epsilon $
for all
![]() $k\in \mathbb {N}$
whenever
$k\in \mathbb {N}$
whenever
![]() $y\in X$
satisfies
$y\in X$
satisfies
![]() $d(x,y)<\delta $
. We say that a point
$d(x,y)<\delta $
. We say that a point
![]() $x\in X$
is (Lyapunov) stable for f if its orbit
$x\in X$
is (Lyapunov) stable for f if its orbit
![]() $(f^n(x))_{n\in \mathbb {N}\cup \{0\}}$
is (Lyapunov) stable. The following two theorems prove that most fixed points of
$(f^n(x))_{n\in \mathbb {N}\cup \{0\}}$
is (Lyapunov) stable. The following two theorems prove that most fixed points of
![]() $\mathcal {J}_n$
in
$\mathcal {J}_n$
in
![]() $\mathcal {C}(X)$
are not stable for
$\mathcal {C}(X)$
are not stable for
![]() $X=\mathbb {R}$
and
$X=\mathbb {R}$
and
![]() $X=S^1$
, respectively.
$X=S^1$
, respectively.
Theorem 8. Let
![]() $n\in \mathbb {N}$
. If
$n\in \mathbb {N}$
. If
![]() $f\in \mathcal {C}_{\mathrm {id}}(\mathbb {R})$
is non-constant, then f is not stable for
$f\in \mathcal {C}_{\mathrm {id}}(\mathbb {R})$
is non-constant, then f is not stable for
![]() $\mathcal {J}_n$
.
$\mathcal {J}_n$
.
Proof. Let
![]() $f\in \mathcal {C}_{\mathrm {id}}(\mathbb {R})$
be a non-constant map. Then there exist
$f\in \mathcal {C}_{\mathrm {id}}(\mathbb {R})$
be a non-constant map. Then there exist
![]() $a, b\in \mathbb {R}$
with
$a, b\in \mathbb {R}$
with
![]() $a<b$
such that
$a<b$
such that
![]() $[a,b]\subseteq R(f)$
and
$[a,b]\subseteq R(f)$
and
![]() $f|_{[a,b]}=\mathrm {id}$
. For each
$f|_{[a,b]}=\mathrm {id}$
. For each
![]() $\eta>0$
, let
$\eta>0$
, let
![]() $g_\eta :\mathbb {R}\to \mathbb {R}$
be the map defined by
$g_\eta :\mathbb {R}\to \mathbb {R}$
be the map defined by
 $$ \begin{align*} g_\eta(x)=\begin{cases} f(x)&\text{if } x\in (-\infty,a]\cup[b,\infty),\\ a+(x-a)(1-\eta)&\text{if } x\in \bigg[a,\dfrac{a+b}{2}\bigg],\\[6pt] x(1+\eta)-b\eta&\text{if } x\in \bigg[\dfrac{a+b}{2}, b\bigg]. \end{cases} \end{align*} $$
$$ \begin{align*} g_\eta(x)=\begin{cases} f(x)&\text{if } x\in (-\infty,a]\cup[b,\infty),\\ a+(x-a)(1-\eta)&\text{if } x\in \bigg[a,\dfrac{a+b}{2}\bigg],\\[6pt] x(1+\eta)-b\eta&\text{if } x\in \bigg[\dfrac{a+b}{2}, b\bigg]. \end{cases} \end{align*} $$
Then
![]() $g_\eta \in \mathcal {C}(\mathbb {R})$
for each
$g_\eta \in \mathcal {C}(\mathbb {R})$
for each
![]() $\eta>0$
. Consider the metric D on
$\eta>0$
. Consider the metric D on
![]() $\mathcal {C}(\mathbb {R})$
defined as in equations (2.2)–(2.4) with the partition
$\mathcal {C}(\mathbb {R})$
defined as in equations (2.2)–(2.4) with the partition
![]() $\mathbb {R}=\bigcup _{j=1}^{\infty }K_j$
, where
$\mathbb {R}=\bigcup _{j=1}^{\infty }K_j$
, where
 $$ \begin{align*} K_j:=\begin{cases} [a,b]&\text{if } j=1,\\ \bigg[b+\dfrac{j-3}{2},b+\dfrac{j-1}{2}\bigg]&\text{if } j=3,5,\ldots,\\[6pt] \bigg[a-\dfrac{j}{2},a-\dfrac{j-2}{2}\bigg] &\text{if } j=2,4,\ldots. \end{cases} \end{align*} $$
$$ \begin{align*} K_j:=\begin{cases} [a,b]&\text{if } j=1,\\ \bigg[b+\dfrac{j-3}{2},b+\dfrac{j-1}{2}\bigg]&\text{if } j=3,5,\ldots,\\[6pt] \bigg[a-\dfrac{j}{2},a-\dfrac{j-2}{2}\bigg] &\text{if } j=2,4,\ldots. \end{cases} \end{align*} $$
Let
![]() $\epsilon =\min \{({b-a})/{8},\tfrac 12\}$
and for any
$\epsilon =\min \{({b-a})/{8},\tfrac 12\}$
and for any
![]() $\delta>0$
, choose
$\delta>0$
, choose
![]() $\eta _\delta>0$
such that
$\eta _\delta>0$
such that
![]() $\eta _\delta <\min \{{\delta _0}/({b-a}),\tfrac 12\}$
for some
$\eta _\delta <\min \{{\delta _0}/({b-a}),\tfrac 12\}$
for some
![]() $0< \delta _0<\min \{\delta ,\tfrac 12\}$
.
$0< \delta _0<\min \{\delta ,\tfrac 12\}$
.
Claim.
![]() $D(f,g_{\eta _\delta })<\delta $
and
$D(f,g_{\eta _\delta })<\delta $
and
![]() $D(f,g_{\eta _\delta }^{n^{k_0}})\ge \epsilon $
for some
$D(f,g_{\eta _\delta }^{n^{k_0}})\ge \epsilon $
for some
![]() $k_0\in \mathbb {N}$
.
$k_0\in \mathbb {N}$
.
Consider any
![]() $x\in \mathbb {R}$
. If
$x\in \mathbb {R}$
. If
![]() $x\in K_1$
with
$x\in K_1$
with
![]() $x\le ({a+b})/{2}$
, then
$x\le ({a+b})/{2}$
, then
If
![]() $x\in K_1$
with
$x\in K_1$
with
![]() $x>({a+b})/{2}$
, then
$x>({a+b})/{2}$
, then
If
![]() $x\in K_j$
with
$x\in K_j$
with
![]() $j>1$
, then
$j>1$
, then
Therefore,
![]() $\rho _1(f,g_{\eta _\delta })\le \delta _0$
and
$\rho _1(f,g_{\eta _\delta })\le \delta _0$
and
![]() $\rho _j(f,g_{\eta _\delta })=0$
for all
$\rho _j(f,g_{\eta _\delta })=0$
for all
![]() $j>1$
, implying that
$j>1$
, implying that
![]() $\mu _1(f,g_{\eta _\delta }) \le \delta _0$
and
$\mu _1(f,g_{\eta _\delta }) \le \delta _0$
and
![]() $\mu _j(f,g_{\eta _\delta })=0$
for all
$\mu _j(f,g_{\eta _\delta })=0$
for all
![]() $j>1$
. Hence,
$j>1$
. Hence,
![]() $D(f,g_{\eta _\delta })\le \delta _0<\delta $
.
$D(f,g_{\eta _\delta })\le \delta _0<\delta $
.
Now for any
![]() $x\in [a,({a+b})/{2}]$
, we have
$x\in [a,({a+b})/{2}]$
, we have
 $$ \begin{align*} &g_{\eta_\delta}(x)= x(1-\eta_\delta)+a\eta_\delta\ge a(1-\eta_\delta)+a\eta_\delta =a, \\ &g_{\eta_\delta}(x)\le\frac{a+b}{2} (1-\eta_\delta)+a\eta_\delta =\frac{a+b}{2}-\frac{b-a}{2}\eta_\delta<\frac{a+b}{2}, \end{align*} $$
$$ \begin{align*} &g_{\eta_\delta}(x)= x(1-\eta_\delta)+a\eta_\delta\ge a(1-\eta_\delta)+a\eta_\delta =a, \\ &g_{\eta_\delta}(x)\le\frac{a+b}{2} (1-\eta_\delta)+a\eta_\delta =\frac{a+b}{2}-\frac{b-a}{2}\eta_\delta<\frac{a+b}{2}, \end{align*} $$
implying that
![]() $g_{\eta _\delta }(x)\in [a, ({a+b})/{2}]$
. Therefore,
$g_{\eta _\delta }(x)\in [a, ({a+b})/{2}]$
. Therefore,
![]() $g_{\eta _\delta }([a,({a+b})/{2}])\subseteq [a,({a+b})/{2}]$
, and hence by induction,
$g_{\eta _\delta }([a,({a+b})/{2}])\subseteq [a,({a+b})/{2}]$
, and hence by induction,
for every
![]() $x\in [a, ({a+b})/{2}]$
and
$x\in [a, ({a+b})/{2}]$
and
![]() $k\in \mathbb {N}$
. Let
$k\in \mathbb {N}$
. Let
![]() $y=({a+b})/{2}$
. Since
$y=({a+b})/{2}$
. Since
![]() $\eta _\delta \in (0,1)$
, equation (4.14) implies that
$\eta _\delta \in (0,1)$
, equation (4.14) implies that
![]() $g_{\eta _\delta }^k(y)\to a$
as
$g_{\eta _\delta }^k(y)\to a$
as
![]() $k\to \infty $
. So there exists
$k\to \infty $
. So there exists
![]() $N\in \mathbb {N}$
such that
$N\in \mathbb {N}$
such that
![]() $|g_{\eta _\delta }^k(y)-a|<\epsilon $
for all
$|g_{\eta _\delta }^k(y)-a|<\epsilon $
for all
![]() $k\ge N$
. Choose
$k\ge N$
. Choose
![]() $k_0\in \mathbb {N}$
so large that
$k_0\in \mathbb {N}$
so large that
![]() $n^{k_0}>N$
. Then
$n^{k_0}>N$
. Then
![]() $g_{\eta _\delta }^{n^{k_0}}(y)-a<({b-a})/{8}$
, that is,
$g_{\eta _\delta }^{n^{k_0}}(y)-a<({b-a})/{8}$
, that is,
![]() $-g_{\eta _\delta }^{n^{k_0}}(y)>-({7a+b})/{8}$
. Thus,
$-g_{\eta _\delta }^{n^{k_0}}(y)>-({7a+b})/{8}$
. Thus,
and therefore
implying that
This proves that
 $$ \begin{align*} \mu_1(f, g_{\eta_\delta}^{n^{k_0}})=\min\bigg\{\frac{1}{2}, \rho_1(f, g_{\eta_\delta}^{n^{k_0}})\bigg\}\ge \min\bigg\{\frac{1}{2}, \frac{b-a}{8}\bigg\}=\epsilon. \end{align*} $$
$$ \begin{align*} \mu_1(f, g_{\eta_\delta}^{n^{k_0}})=\min\bigg\{\frac{1}{2}, \rho_1(f, g_{\eta_\delta}^{n^{k_0}})\bigg\}\ge \min\bigg\{\frac{1}{2}, \frac{b-a}{8}\bigg\}=\epsilon. \end{align*} $$
Therefore, the claim holds, and hence f is not stable for
![]() $\mathcal {J}_n$
.
$\mathcal {J}_n$
.
Theorem 9. Let
![]() $n\in \mathbb {N}$
and
$n\in \mathbb {N}$
and
![]() $f\in \mathcal {C}_{\mathrm {id}}(S^1)$
, consisting of all continuous self-maps of
$f\in \mathcal {C}_{\mathrm {id}}(S^1)$
, consisting of all continuous self-maps of
![]() $S^1$
which are the identity on their range. Then f is stable for
$S^1$
which are the identity on their range. Then f is stable for
![]() $\mathcal {J}_n$
if and only if f is a constant map on
$\mathcal {J}_n$
if and only if f is a constant map on
![]() $S^1$
.
$S^1$
.
Proof. Let
![]() $n\in \mathbb {N}$
and
$n\in \mathbb {N}$
and
![]() $f\in \mathcal {C}_{\mathrm {id}}(S^1)$
be a constant map on
$f\in \mathcal {C}_{\mathrm {id}}(S^1)$
be a constant map on
![]() $S^1$
. For given
$S^1$
. For given
![]() $\epsilon>0$
, choose
$\epsilon>0$
, choose
![]() $\delta =\epsilon $
. Then for every
$\delta =\epsilon $
. Then for every
![]() $k\in \mathbb {N}$
and
$k\in \mathbb {N}$
and
![]() $g\in \mathcal {C}(S^1)$
with
$g\in \mathcal {C}(S^1)$
with
![]() $\rho (f,g)<\delta $
, we have
$\rho (f,g)<\delta $
, we have
implying
![]() $\rho (f,g^k)<\epsilon $
, and hence in particular
$\rho (f,g^k)<\epsilon $
, and hence in particular
![]() $\rho (f^{n^k},g^{n^k})<\epsilon $
. Therefore, f is stable.
$\rho (f^{n^k},g^{n^k})<\epsilon $
. Therefore, f is stable.
Conversely, suppose that
![]() $f\in \mathcal {C}_{\mathrm {id}}(S^1)$
is a non-constant map on
$f\in \mathcal {C}_{\mathrm {id}}(S^1)$
is a non-constant map on
![]() $S^1$
. Then
$S^1$
. Then
![]() $f|_{R(f)}=\mathrm {id}$
such that either
$f|_{R(f)}=\mathrm {id}$
such that either
![]() $R(f)=S^1$
or
$R(f)=S^1$
or
![]() $R(f)=[z_1,z_2]$
for some
$R(f)=[z_1,z_2]$
for some
![]() $z_1=e^{it_1}$
,
$z_1=e^{it_1}$
,
![]() $z_2=e^{it_2}\in S^1$
with
$z_2=e^{it_2}\in S^1$
with
![]() $0\le t_1<t_2< 2\pi $
. For each
$0\le t_1<t_2< 2\pi $
. For each
![]() $\eta>0$
, let
$\eta>0$
, let
![]() $g_\eta :S^1\to S^1$
be the map defined by
$g_\eta :S^1\to S^1$
be the map defined by
 $$ \begin{align*} g_\eta(e^{it})=\begin{cases} f(e^{it})&\text{if } t\in [0,2\pi)\setminus[t_1,t_2],\\ e^{i[t_1+(t-t_1)(1-\eta)]}&\text{if } t\in \bigg[t_1,\dfrac{t_1+t_2}{2}\bigg],\\[6pt] e^{i[t(1+\eta)- t_2\eta]}&\text{if } t\in \bigg[\dfrac{t_1+t_2}{2}, t_2\bigg]. \end{cases} \end{align*} $$
$$ \begin{align*} g_\eta(e^{it})=\begin{cases} f(e^{it})&\text{if } t\in [0,2\pi)\setminus[t_1,t_2],\\ e^{i[t_1+(t-t_1)(1-\eta)]}&\text{if } t\in \bigg[t_1,\dfrac{t_1+t_2}{2}\bigg],\\[6pt] e^{i[t(1+\eta)- t_2\eta]}&\text{if } t\in \bigg[\dfrac{t_1+t_2}{2}, t_2\bigg]. \end{cases} \end{align*} $$
Then
![]() $g_\eta \in \mathcal {C}(S^1)$
for each
$g_\eta \in \mathcal {C}(S^1)$
for each
![]() $\eta>0$
. Let
$\eta>0$
. Let
![]() $\epsilon =({t_2-t_1})/{2\sqrt {2}\pi }$
and for any
$\epsilon =({t_2-t_1})/{2\sqrt {2}\pi }$
and for any
![]() $\delta>0$
, choose
$\delta>0$
, choose
![]() $\eta _\delta>0$
such that
$\eta _\delta>0$
such that
![]() $\eta _\delta <\min \{{2\delta _0}/({t_2-t_1}),1\}$
for some
$\eta _\delta <\min \{{2\delta _0}/({t_2-t_1}),1\}$
for some
![]() $0<\delta _0<\delta $
.
$0<\delta _0<\delta $
.
Claim.
![]() $\rho (f,g_{\eta _\delta })<\delta $
and
$\rho (f,g_{\eta _\delta })<\delta $
and
![]() $\rho (f,g_{\eta _\delta }^{n^{k_0}})\ge \epsilon $
for some
$\rho (f,g_{\eta _\delta }^{n^{k_0}})\ge \epsilon $
for some
![]() $k_0\in \mathbb {N}$
.
$k_0\in \mathbb {N}$
.
Consider any
![]() $t\in [0,2\pi )$
. If
$t\in [0,2\pi )$
. If
![]() $t\in [0,2\pi )\setminus [t_1,t_2]$
, then
$t\in [0,2\pi )\setminus [t_1,t_2]$
, then
If
![]() $t\in (t_1, ({t_1+t_2})/{2})$
, then
$t\in (t_1, ({t_1+t_2})/{2})$
, then
 $$ \begin{align*} |f(e^{it})-g_{\eta_\delta}(e^{it})|&=|e^{it}-e^{i[t_1+(t-t_1)(1-\eta_\delta)]}|\\ &=|1-e^{i\eta_\delta(t_1-t)}|\\ &\le 2\bigg|\sin\bigg(\dfrac{\eta_\delta(t_1-t)}{2}\bigg)\bigg|\\ &\le |\eta_\delta(t_1-t)|=(t-t_1)\eta_\delta<\dfrac{t_2-t_1}{2} \dfrac{2\delta_0}{t_2-t_1}=\delta_0. \end{align*} $$
$$ \begin{align*} |f(e^{it})-g_{\eta_\delta}(e^{it})|&=|e^{it}-e^{i[t_1+(t-t_1)(1-\eta_\delta)]}|\\ &=|1-e^{i\eta_\delta(t_1-t)}|\\ &\le 2\bigg|\sin\bigg(\dfrac{\eta_\delta(t_1-t)}{2}\bigg)\bigg|\\ &\le |\eta_\delta(t_1-t)|=(t-t_1)\eta_\delta<\dfrac{t_2-t_1}{2} \dfrac{2\delta_0}{t_2-t_1}=\delta_0. \end{align*} $$
If
![]() $t\in [({t_1+t_2})/{2},t_2)$
, then by a similar argument, we have
$t\in [({t_1+t_2})/{2},t_2)$
, then by a similar argument, we have
![]() $|f(e^{it})-g_{\eta _\delta }(e^{it})|<\delta _0$
. Therefore,
$|f(e^{it})-g_{\eta _\delta }(e^{it})|<\delta _0$
. Therefore,
![]() $|f(e^{it})-g_{\eta _\delta }(e^{it})|< \delta _0$
for all
$|f(e^{it})-g_{\eta _\delta }(e^{it})|< \delta _0$
for all
![]() $t\in [0,2\pi )$
and hence
$t\in [0,2\pi )$
and hence
![]() $\rho (f,g_{\eta _\delta })\le \delta _0<\delta $
.
$\rho (f,g_{\eta _\delta })\le \delta _0<\delta $
.
Now for any
![]() $t\in [t_1,({t_1+t_2})/{2}]$
, we have
$t\in [t_1,({t_1+t_2})/{2}]$
, we have
 $$ \begin{align*} t_1=t_1(1-\eta_\delta)+t_1\eta_\delta &\le t(1-\eta_\delta)+t_1\eta_\delta\\ &=t_1+(t-t_1)(1-\eta_\delta)\\ &\le\frac{t_1+t_2}{2} (1-\eta_\delta)+t_1\eta_\delta\\ &=\frac{t_1+t_2}{2}-\frac{t_2-t_1}{2}\eta_\delta<\frac{t_1+t_2}{2}, \end{align*} $$
$$ \begin{align*} t_1=t_1(1-\eta_\delta)+t_1\eta_\delta &\le t(1-\eta_\delta)+t_1\eta_\delta\\ &=t_1+(t-t_1)(1-\eta_\delta)\\ &\le\frac{t_1+t_2}{2} (1-\eta_\delta)+t_1\eta_\delta\\ &=\frac{t_1+t_2}{2}-\frac{t_2-t_1}{2}\eta_\delta<\frac{t_1+t_2}{2}, \end{align*} $$
implying
![]() $g_{\eta _\delta }(e^{it})\in [z_1, w]$
, where
$g_{\eta _\delta }(e^{it})\in [z_1, w]$
, where
![]() $w=e^{i({t_1+t_2})/{2}}$
. Therefore,
$w=e^{i({t_1+t_2})/{2}}$
. Therefore,
![]() $g_{\eta _\delta }([z_1,w])\subseteq [z_1,w]$
. Hence, it can be shown by induction that
$g_{\eta _\delta }([z_1,w])\subseteq [z_1,w]$
. Hence, it can be shown by induction that
![]() $g_{\eta _\delta }^k(e^{it})=e^{i[t_1+(t-t_1)(1-\eta _\delta )^k]}$
for every
$g_{\eta _\delta }^k(e^{it})=e^{i[t_1+(t-t_1)(1-\eta _\delta )^k]}$
for every
![]() $t\in [t_1, ({t_1+t_2})/{2}]$
and
$t\in [t_1, ({t_1+t_2})/{2}]$
and
![]() $k\in \mathbb {N}$
. Also,
$k\in \mathbb {N}$
. Also,
![]() $\sin ({t}/{2})\ge {t}/{\pi }$
for all
$\sin ({t}/{2})\ge {t}/{\pi }$
for all
![]() $t\in [0,\pi ],$
and therefore,
$t\in [0,\pi ],$
and therefore,
 $$ \begin{align} |e^{it}-1|=\sqrt{2}\sin \bigg(\dfrac{t}{2}\bigg)\ge\dfrac{\sqrt{2}t}{\pi} \quad \text{for all } t\in [0,\pi]. \end{align} $$
$$ \begin{align} |e^{it}-1|=\sqrt{2}\sin \bigg(\dfrac{t}{2}\bigg)\ge\dfrac{\sqrt{2}t}{\pi} \quad \text{for all } t\in [0,\pi]. \end{align} $$
Now for each
![]() $k\in \mathbb {N}$
, we have
$k\in \mathbb {N}$
, we have
 $$ \begin{align} |f(w)-g_{\eta_\delta}^k(w)|&=|e^{i({t_1+t_2})/{2}}-e^{i[t_1+(({t_1+t_2})/{2}-t_1)(1-\eta_\delta)^k]}| \nonumber\\ &=|1-e^{-i[({t_2-t_1})/{2}(1-(1-\eta_\delta)^k)]}| \nonumber\\ &=|e^{i[({t_2-t_1})/{2}(1-(1-\eta_\delta)^k)]}-1| \end{align} $$
$$ \begin{align} |f(w)-g_{\eta_\delta}^k(w)|&=|e^{i({t_1+t_2})/{2}}-e^{i[t_1+(({t_1+t_2})/{2}-t_1)(1-\eta_\delta)^k]}| \nonumber\\ &=|1-e^{-i[({t_2-t_1})/{2}(1-(1-\eta_\delta)^k)]}| \nonumber\\ &=|e^{i[({t_2-t_1})/{2}(1-(1-\eta_\delta)^k)]}-1| \end{align} $$
and
implying by equation (4.15) that
 $$ \begin{align*} |e^{i[({t_2-t_1})/{2}(1-(1-\eta_\delta)^k)]}-1|&\ge \dfrac{\sqrt{2}}{\pi}\cdot\frac{t_2-t_1}{2}[1-(1-\eta_\delta)^k]\\ &=\dfrac{t_2-t_1}{\sqrt{2}\pi}[1-(1-\eta_\delta)^k], \end{align*} $$
$$ \begin{align*} |e^{i[({t_2-t_1})/{2}(1-(1-\eta_\delta)^k)]}-1|&\ge \dfrac{\sqrt{2}}{\pi}\cdot\frac{t_2-t_1}{2}[1-(1-\eta_\delta)^k]\\ &=\dfrac{t_2-t_1}{\sqrt{2}\pi}[1-(1-\eta_\delta)^k], \end{align*} $$
for each
![]() $k\in \mathbb {N}$
. Then equation (4.16) implies that
$k\in \mathbb {N}$
. Then equation (4.16) implies that
for each
![]() $k\in \mathbb {N}$
. Since
$k\in \mathbb {N}$
. Since
![]() $1-(1-\eta _\delta )^k\rightarrow 1$
as
$1-(1-\eta _\delta )^k\rightarrow 1$
as
![]() $k\rightarrow \infty $
, there exists
$k\rightarrow \infty $
, there exists
![]() $N\in \mathbb {N}$
such that
$N\in \mathbb {N}$
such that
![]() $(1-\eta _\delta )^k<\tfrac 12$
for all
$(1-\eta _\delta )^k<\tfrac 12$
for all
![]() $k\ge N$
. Choose
$k\ge N$
. Choose
![]() $k_0$
sufficiently large such that
$k_0$
sufficiently large such that
![]() $n^{k_0}>N$
. Then
$n^{k_0}>N$
. Then
![]() $1-(1-\eta _\delta )^{n^{k_0}}> \tfrac 12$
, and therefore from equation (4.17), we have
$1-(1-\eta _\delta )^{n^{k_0}}> \tfrac 12$
, and therefore from equation (4.17), we have
which implies that
This proves the claim, from which it follows that f is not stable, which is a contradiction. Hence, f is a constant map on
![]() $S^1$
.
$S^1$
.
As defined in [Reference Holmgren10], a discrete semi-dynamical system
![]() $(X,f)$
, where X is a metric space equipped with the metric d, is said to be topologically transitive if for every pair of open sets
$(X,f)$
, where X is a metric space equipped with the metric d, is said to be topologically transitive if for every pair of open sets
![]() $U, V$
in X, there exist
$U, V$
in X, there exist
![]() $x \in U$
and
$x \in U$
and
![]() $n \in \mathbb {N}$
such that
$n \in \mathbb {N}$
such that
![]() $f^n(x)\in V$
. Here, f is said to be sensitively dependent on initial conditions if there exists
$f^n(x)\in V$
. Here, f is said to be sensitively dependent on initial conditions if there exists
![]() $\delta>0$
such that for every
$\delta>0$
such that for every
![]() $x \in X$
and every
$x \in X$
and every
![]() $\epsilon>0$
, there exist
$\epsilon>0$
, there exist
![]() $y \in X$
and
$y \in X$
and
![]() $n \in \mathbb {N}$
such that
$n \in \mathbb {N}$
such that
![]() $d(x,y)<\epsilon $
and
$d(x,y)<\epsilon $
and
![]() $d(f^n(x), f^n(y))>\delta $
. As defined in [Reference Devaney8], f is said to be chaotic in Devaney’s sense if: (i) the set of periodic points of f is dense in X; (ii) f is topologically transitive; and (iii) f exhibits sensitive dependence on initial conditions. Since
$d(f^n(x), f^n(y))>\delta $
. As defined in [Reference Devaney8], f is said to be chaotic in Devaney’s sense if: (i) the set of periodic points of f is dense in X; (ii) f is topologically transitive; and (iii) f exhibits sensitive dependence on initial conditions. Since
![]() $\mathrm {Per}(\mathcal {J}_n;\mathcal {C}(\mathbb {R}))$
is not dense in
$\mathrm {Per}(\mathcal {J}_n;\mathcal {C}(\mathbb {R}))$
is not dense in
![]() $\mathcal {C}(\mathbb {R})$
, as seen in §3,
$\mathcal {C}(\mathbb {R})$
, as seen in §3,
![]() $\mathcal {J}_n$
is not chaotic
$\mathcal {J}_n$
is not chaotic
![]() $\mathcal {C}(\mathbb {R})$
for
$\mathcal {C}(\mathbb {R})$
for
![]() $n\ge 2$
. Also, since
$n\ge 2$
. Also, since
![]() $S^1$
is compact, by [Reference Veerapazham, Gopalakrishna and Zhang23, Theorem 5.1],
$S^1$
is compact, by [Reference Veerapazham, Gopalakrishna and Zhang23, Theorem 5.1],
![]() $\mathcal {J}_n$
is not chaotic on
$\mathcal {J}_n$
is not chaotic on
![]() $\mathcal {C}(S^1)$
for
$\mathcal {C}(S^1)$
for
![]() $n\ge 2$
. However,
$n\ge 2$
. However,
![]() $\mathcal {J}_1$
is also not chaotic on
$\mathcal {J}_1$
is also not chaotic on
![]() $\mathcal {C}(\mathbb {R})$
and
$\mathcal {C}(\mathbb {R})$
and
![]() $\mathcal {C}(S^1)$
since it is not sensitively dependent on initial conditions. Thus, although we see that all orbits of
$\mathcal {C}(S^1)$
since it is not sensitively dependent on initial conditions. Thus, although we see that all orbits of
![]() $\mathcal {J}_n$
in
$\mathcal {J}_n$
in
![]() $\mathcal {C}(\mathbb {R})$
and
$\mathcal {C}(\mathbb {R})$
and
![]() $\mathcal {C}(S^1)$
are bounded but most of the fixed points are unstable, which actually exhibits a complicated behavior of
$\mathcal {C}(S^1)$
are bounded but most of the fixed points are unstable, which actually exhibits a complicated behavior of
![]() $\mathcal {J}_n$
, the complicated behavior is not chaotic. The following examples show how complicated an orbit of
$\mathcal {J}_n$
, the complicated behavior is not chaotic. The following examples show how complicated an orbit of
![]() $\mathcal {J}_n$
can be.
$\mathcal {J}_n$
can be.
Example 4. Let
![]() $f:\mathbb {R}\to \mathbb {R}$
be the map defined by
$f:\mathbb {R}\to \mathbb {R}$
be the map defined by
 $$ \begin{align*} f(x)=\begin{cases} 0&\text{if } x\le 0,\\ x&\text{if }0\le x\le 1,\\ 1&\text{if } x\ge 0. \end{cases} \end{align*} $$
$$ \begin{align*} f(x)=\begin{cases} 0&\text{if } x\le 0,\\ x&\text{if }0\le x\le 1,\\ 1&\text{if } x\ge 0. \end{cases} \end{align*} $$
Let
![]() $n=2$
,
$n=2$
,
![]() $\epsilon =\tfrac 18$
,
$\epsilon =\tfrac 18$
,
![]() $\delta =0.13$
,
$\delta =0.13$
,
![]() $\delta _0=0.07$
,
$\delta _0=0.07$
,
![]() $\eta _\delta =0.04$
, and
$\eta _\delta =0.04$
, and
![]() $g_2$
be the map
$g_2$
be the map
![]() $g_{\eta _\delta }$
as defined in Theorem 8 with
$g_{\eta _\delta }$
as defined in Theorem 8 with
![]() $a=0$
and
$a=0$
and
![]() $b=1$
. Define the maps
$b=1$
. Define the maps
![]() $g_1$
,
$g_1$
,
![]() $g_3:\mathbb {R}\to \mathbb {R}$
by
$g_3:\mathbb {R}\to \mathbb {R}$
by
 $$ \begin{align*} g_1(x)=\begin{cases} 0&\text{if } x\le 0,\\ 0.99x&\text{if } 0\le x\le 1,\\ 0.99&\text{if } x\ge 1, \end{cases}\quad \text{and} \quad g_3(x)=\begin{cases} 0&\text{if } x\le 0,\\ 1.1x&\text{if } 0\le x \le 0.5,\\ x+0.05&\text{if } 0.5\le x\le 0.55,\\ -2x+1.7&\text{if } 0.55\le x\le 0.6,\\ 1.25x-0.25&\text{if } 0.6\le x\le 1,\\ 1&\text{if } x\ge 1. \end{cases} \end{align*} $$
$$ \begin{align*} g_1(x)=\begin{cases} 0&\text{if } x\le 0,\\ 0.99x&\text{if } 0\le x\le 1,\\ 0.99&\text{if } x\ge 1, \end{cases}\quad \text{and} \quad g_3(x)=\begin{cases} 0&\text{if } x\le 0,\\ 1.1x&\text{if } 0\le x \le 0.5,\\ x+0.05&\text{if } 0.5\le x\le 0.55,\\ -2x+1.7&\text{if } 0.55\le x\le 0.6,\\ 1.25x-0.25&\text{if } 0.6\le x\le 1,\\ 1&\text{if } x\ge 1. \end{cases} \end{align*} $$
Then
![]() $f\in \mathrm {Fix}(\mathcal {J}_2; \mathcal {C}(\mathbb {R}))$
and
$f\in \mathrm {Fix}(\mathcal {J}_2; \mathcal {C}(\mathbb {R}))$
and
![]() $g_1, g_2, g_3 \in \mathcal {C}(\mathbb {R})$
. Consider the metric D on
$g_1, g_2, g_3 \in \mathcal {C}(\mathbb {R})$
. Consider the metric D on
![]() $\mathcal {C}(\mathbb {R})$
defined as in equations (2.2)–(2.4) with the partition
$\mathcal {C}(\mathbb {R})$
defined as in equations (2.2)–(2.4) with the partition
![]() $\mathbb {R}=\bigcup _{j=1}^{\infty }K_j$
, where
$\mathbb {R}=\bigcup _{j=1}^{\infty }K_j$
, where
 $$ \begin{align*} K_j:=\begin{cases} [0,1]&\text{if } j=1,\\ \bigg[-\dfrac{j-1}{2},-\dfrac{j-1}{2}+1\bigg]&\text{if } j=3,5,\ldots,\\[6pt] \bigg[\dfrac{j}{2},\dfrac{j}{2}+1\bigg] &\text{if } j=2,4,\ldots. \end{cases} \end{align*} $$
$$ \begin{align*} K_j:=\begin{cases} [0,1]&\text{if } j=1,\\ \bigg[-\dfrac{j-1}{2},-\dfrac{j-1}{2}+1\bigg]&\text{if } j=3,5,\ldots,\\[6pt] \bigg[\dfrac{j}{2},\dfrac{j}{2}+1\bigg] &\text{if } j=2,4,\ldots. \end{cases} \end{align*} $$
An easy computation shows that
![]() $D(g_j,f)<\delta $
for all
$D(g_j,f)<\delta $
for all
![]() $j=1,2,3$
. However,
$j=1,2,3$
. However,
![]() $g_1^{2^6}(0.4)=0.2102$
,
$g_1^{2^6}(0.4)=0.2102$
,
![]() $g_2^{2^4}(0.4)=0.2082$
, and
$g_2^{2^4}(0.4)=0.2082$
, and
![]() $g_3^{2^3}(0.4)=0.5796$
, implying that
$g_3^{2^3}(0.4)=0.5796$
, implying that
![]() $D(g_1^{2^6} f)>\epsilon $
,
$D(g_1^{2^6} f)>\epsilon $
,
![]() $D(g_2^{2^4} f)>\epsilon $
, and
$D(g_2^{2^4} f)>\epsilon $
, and
![]() $D(g_3^{2^3}, f)>\epsilon $
. This illustrates the claim in the proof of Theorem 8 for f for the above-mentioned specific choices of
$D(g_3^{2^3}, f)>\epsilon $
. This illustrates the claim in the proof of Theorem 8 for f for the above-mentioned specific choices of
![]() $\delta $
,
$\delta $
,
![]() $\delta _0$
, and
$\delta _0$
, and
![]() $\eta _\delta $
with
$\eta _\delta $
with
![]() $\epsilon =\tfrac 18$
. Indeed, f is not stable for
$\epsilon =\tfrac 18$
. Indeed, f is not stable for
![]() $\mathcal {J}_2$
as seen from Theorem 8.
$\mathcal {J}_2$
as seen from Theorem 8.
To illustrate the complexity of
![]() $\mathcal {J}_2$
, we investigate the asymptotic behavior of the orbits of
$\mathcal {J}_2$
, we investigate the asymptotic behavior of the orbits of
![]() $g_1, g_2$
, and
$g_1, g_2$
, and
![]() $g_3$
. We have
$g_3$
. We have
 $$ \begin{align*} g_1^k(x)=\begin{cases} 0&\text{if } x\le 0,\\ 0.99^kx&\text{if } 0\le x\le 1,\\ 0.99^k&\text{if } x\ge 1, \end{cases} \end{align*} $$
$$ \begin{align*} g_1^k(x)=\begin{cases} 0&\text{if } x\le 0,\\ 0.99^kx&\text{if } 0\le x\le 1,\\ 0.99^k&\text{if } x\ge 1, \end{cases} \end{align*} $$
for all
![]() $k\in \mathbb {N}$
. Therefore, the sequence of maps
$k\in \mathbb {N}$
. Therefore, the sequence of maps
![]() $(g_1^k)_{k\in \mathbb {N}}$
and hence the orbit
$(g_1^k)_{k\in \mathbb {N}}$
and hence the orbit
![]() $(g_1^{2^k})_{k\in \mathbb {N}\cup \{0\}}$
of
$(g_1^{2^k})_{k\in \mathbb {N}\cup \{0\}}$
of
![]() $g_1$
converges uniformly to the zero map on
$g_1$
converges uniformly to the zero map on
![]() $\mathbb {R}$
. As seen in the proof of Theorem 8,
$\mathbb {R}$
. As seen in the proof of Theorem 8,
![]() $g_2^k(x)\to 0 ~\text {as}~k\to \infty $
, for each
$g_2^k(x)\to 0 ~\text {as}~k\to \infty $
, for each
![]() $x\in [0,0.5]$
. Also, for each
$x\in [0,0.5]$
. Also, for each
![]() $x\in [0.5,1)$
, there exists
$x\in [0.5,1)$
, there exists
![]() $k_x\in \mathbb {N}$
such that
$k_x\in \mathbb {N}$
such that
![]() $g_2^{k_x}(x)\in [0,0.5]$
. Further,
$g_2^{k_x}(x)\in [0,0.5]$
. Further,
 $$ \begin{align*} g_2^k(x)=\begin{cases} 0&\text{if } x\le 0,\\ 1&\text{if } x\ge 1, \end{cases} \end{align*} $$
$$ \begin{align*} g_2^k(x)=\begin{cases} 0&\text{if } x\le 0,\\ 1&\text{if } x\ge 1, \end{cases} \end{align*} $$
for all
![]() $k\in \mathbb {N}$
. Thus, the sequence of maps
$k\in \mathbb {N}$
. Thus, the sequence of maps
![]() $(g_2^k)_{k\in \mathbb {N}}$
and hence the orbit
$(g_2^k)_{k\in \mathbb {N}}$
and hence the orbit
![]() $(g_2^{2^k})_{k\in \mathbb {N}\cup \{0\}}$
of
$(g_2^{2^k})_{k\in \mathbb {N}\cup \{0\}}$
of
![]() $g_2$
converges pointwise to the discontinuous map
$g_2$
converges pointwise to the discontinuous map
![]() $f_2:\mathbb {R}\to \mathbb {R}$
defined by
$f_2:\mathbb {R}\to \mathbb {R}$
defined by
 $$ \begin{align*} f_2(x)=\begin{cases} 0&\text{if } x<1,\\ 1&\text{if } x\ge 1. \end{cases} \end{align*} $$
$$ \begin{align*} f_2(x)=\begin{cases} 0&\text{if } x<1,\\ 1&\text{if } x\ge 1. \end{cases} \end{align*} $$
The point
![]() $x=0.5$
is a
$x=0.5$
is a
![]() $3$
-periodic point of
$3$
-periodic point of
![]() $g_3$
and therefore, the orbit
$g_3$
and therefore, the orbit
![]() $(g_3^{2^k})_{k\in \mathbb {N}\cup \{0\}}$
of
$(g_3^{2^k})_{k\in \mathbb {N}\cup \{0\}}$
of
![]() $g_3$
does not converge. In fact, by [Reference Li and Yorke16, Theorem 1],
$g_3$
does not converge. In fact, by [Reference Li and Yorke16, Theorem 1],
![]() $g_3$
is chaotic in the sense of Li and Yorke. However,
$g_3$
is chaotic in the sense of Li and Yorke. However,
![]() $g_3([0,1])\subseteq [0,1]$
, implying that
$g_3([0,1])\subseteq [0,1]$
, implying that
![]() $g_3$
is not topologically transitive and therefore is not chaotic in the sense of Devaney.
$g_3$
is not topologically transitive and therefore is not chaotic in the sense of Devaney.
Thus, although all the orbits of
![]() $\mathcal {J}_2$
in
$\mathcal {J}_2$
in
![]() $\mathcal {C}(\mathbb {R})$
are bounded, it is possible that an orbit may not converge or, even if it converges, the limit function may not be continuous. Furthermore, the choice of
$\mathcal {C}(\mathbb {R})$
are bounded, it is possible that an orbit may not converge or, even if it converges, the limit function may not be continuous. Furthermore, the choice of
![]() $\delta =0.13$
is not special. Indeed, we can construct maps in
$\delta =0.13$
is not special. Indeed, we can construct maps in
![]() $\mathcal {C}(\mathbb {R})$
that are similar to those of
$\mathcal {C}(\mathbb {R})$
that are similar to those of
![]() $g_1$
,
$g_1$
,
![]() $g_2$
, and
$g_2$
, and
![]() $g_3$
in each
$g_3$
in each
![]() $\delta $
-neighborhood of f.
$\delta $
-neighborhood of f.
Example 5. Let f be the identity map on
![]() $S^1$
. Let
$S^1$
. Let
![]() $n=2$
,
$n=2$
,
![]() $\epsilon =\tfrac 18$
,
$\epsilon =\tfrac 18$
,
![]() $\delta =0.15$
,
$\delta =0.15$
,
![]() $\delta _0=0.07$
,
$\delta _0=0.07$
,
![]() $\eta _\delta =0.05$
, and
$\eta _\delta =0.05$
, and
![]() $g_2$
be the map
$g_2$
be the map
![]() $g_{\eta _\delta }$
as defined in Theorem 9 with
$g_{\eta _\delta }$
as defined in Theorem 9 with
![]() $t_1=0$
and
$t_1=0$
and
![]() $t_2={\pi }/{2}$
. Define the maps
$t_2={\pi }/{2}$
. Define the maps
![]() $g_1$
,
$g_1$
,
![]() $g_3:S^1\to S^1$
by
$g_3:S^1\to S^1$
by
![]() $g_1(e^{it})=e^{0.9it}$
for all
$g_1(e^{it})=e^{0.9it}$
for all
![]() $t\in [0,2\pi ),$
and
$t\in [0,2\pi ),$
and
Then
![]() $f\in \mathrm {Fix}(\mathcal {J}_2; \mathcal {C}(S^1))$
and
$f\in \mathrm {Fix}(\mathcal {J}_2; \mathcal {C}(S^1))$
and
![]() $g_1, g_2, g_3 \in \mathcal {C}(S^1)$
. A computation as in Theorem 9 shows that
$g_1, g_2, g_3 \in \mathcal {C}(S^1)$
. A computation as in Theorem 9 shows that
![]() $\rho (g_2,f)<\delta $
. However,
$\rho (g_2,f)<\delta $
. However,
 $$ \begin{align*} |g_2^{2^4}(e^{i{\pi}/{4}})-e^{i{\pi}/{4}}|&=|1-e^{i{\pi}/{4}(1-0.95^{2^4})}|\\ &\ge \frac{1}{2\sqrt{2}}(1-0.95^{2^4})\quad(\text{using equation~}(4.15))\\ &\ge\frac{1}{4\sqrt{2}}>\epsilon, \end{align*} $$
$$ \begin{align*} |g_2^{2^4}(e^{i{\pi}/{4}})-e^{i{\pi}/{4}}|&=|1-e^{i{\pi}/{4}(1-0.95^{2^4})}|\\ &\ge \frac{1}{2\sqrt{2}}(1-0.95^{2^4})\quad(\text{using equation~}(4.15))\\ &\ge\frac{1}{4\sqrt{2}}>\epsilon, \end{align*} $$
implying that
![]() $\rho (g_2^{2^4}, f)>\epsilon $
. Indeed, f is not stable for
$\rho (g_2^{2^4}, f)>\epsilon $
. Indeed, f is not stable for
![]() $\mathcal {J}_2$
as seen from Theorem 9.
$\mathcal {J}_2$
as seen from Theorem 9.
To illustrate the complexity of iteration operator
![]() $\mathcal {J}_2$
, we investigate the asymptotic behavior of the orbits of
$\mathcal {J}_2$
, we investigate the asymptotic behavior of the orbits of
![]() $g_1, g_2$
, and
$g_1, g_2$
, and
![]() $g_3$
. We have
$g_3$
. We have
![]() $g_1^k(e^{it})=e^{0.9^kit} \text { for all} k\in \mathbb {N}~\text {and for all } t\in [0,2\pi ).$
Therefore, the sequence of maps
$g_1^k(e^{it})=e^{0.9^kit} \text { for all} k\in \mathbb {N}~\text {and for all } t\in [0,2\pi ).$
Therefore, the sequence of maps
![]() $(g_1^k)_{k\in \mathbb {N}}$
and hence the orbit
$(g_1^k)_{k\in \mathbb {N}}$
and hence the orbit
![]() $(g_1^{2^k})_{k\in \mathbb {N}\cup \{0\}}$
of
$(g_1^{2^k})_{k\in \mathbb {N}\cup \{0\}}$
of
![]() $g_1$
converge uniformly to the constant map
$g_1$
converge uniformly to the constant map
![]() $f_1:S^1 \to S^1$
defined by
$f_1:S^1 \to S^1$
defined by
![]() $f_2(e^{it})=1$
for all
$f_2(e^{it})=1$
for all
![]() $t\in [0,2\pi )$
. As noted in the proof of Theorem 9,
$t\in [0,2\pi )$
. As noted in the proof of Theorem 9,
![]() $g_2^k(e^{it})\to 1 ~\text {as} k\to \infty $
, for each
$g_2^k(e^{it})\to 1 ~\text {as} k\to \infty $
, for each
![]() $t\in [0,{\pi }/{4}]$
. Also, for each
$t\in [0,{\pi }/{4}]$
. Also, for each
![]() $t\in [{\pi }/{4},{\pi }/{2})$
, there exists
$t\in [{\pi }/{4},{\pi }/{2})$
, there exists
![]() $k_t\in \mathbb {N}$
such that
$k_t\in \mathbb {N}$
such that
![]() $\arg (g_2^{k_t}(e^{it}))\in [0,{\pi }/{4}]$
. Moreover,
$\arg (g_2^{k_t}(e^{it}))\in [0,{\pi }/{4}]$
. Moreover,
![]() $g_2^k(e^{it})=e^{it} \text { for all } k\in \mathbb {N}$
and
$g_2^k(e^{it})=e^{it} \text { for all } k\in \mathbb {N}$
and
![]() $\text { for all } t\in [{\pi }/{2}, 2\pi )$
. Thus, the sequence of maps
$\text { for all } t\in [{\pi }/{2}, 2\pi )$
. Thus, the sequence of maps
![]() $(g_2^k)_{k\in \mathbb {N}}$
and hence the orbit
$(g_2^k)_{k\in \mathbb {N}}$
and hence the orbit
![]() $(g_2^{2^k})_{k\in \mathbb {N}\cup \{0\}}$
of
$(g_2^{2^k})_{k\in \mathbb {N}\cup \{0\}}$
of
![]() $g_2$
converge pointwise to the discontinuous map
$g_2$
converge pointwise to the discontinuous map
![]() $f_2:S^1\to S^1$
defined by
$f_2:S^1\to S^1$
defined by
 $$ \begin{align*} f_2(e^{it})=\begin{cases} 1&\text{if } 0\le t<\dfrac{\pi}{2},\\ e^{it}&\text{if } \dfrac{\pi}{2}\le t<2\pi. \end{cases} \end{align*} $$
$$ \begin{align*} f_2(e^{it})=\begin{cases} 1&\text{if } 0\le t<\dfrac{\pi}{2},\\ e^{it}&\text{if } \dfrac{\pi}{2}\le t<2\pi. \end{cases} \end{align*} $$
The map
![]() $g_3$
is a
$g_3$
is a
![]() $3$
-periodic point of
$3$
-periodic point of
![]() $\mathcal {J}_2$
and therefore the orbit
$\mathcal {J}_2$
and therefore the orbit
![]() $(g_3^{2^k})_{k\in \mathbb {N}\cup \{0\}}$
of
$(g_3^{2^k})_{k\in \mathbb {N}\cup \{0\}}$
of
![]() $g_3$
converges to the periodic orbit
$g_3$
converges to the periodic orbit
![]() $\{g_3, g_3^2, g_3^{2^2}\}$
.
$\{g_3, g_3^2, g_3^{2^2}\}$
.
Thus, similar to
![]() $\mathcal {C}(\mathbb {R})$
, although all the orbits of
$\mathcal {C}(\mathbb {R})$
, although all the orbits of
![]() $\mathcal {J}_2$
in
$\mathcal {J}_2$
in
![]() $\mathcal {C}(S^1)$
are bounded, it is possible that an orbit may not converge or, even if it converges, the limit function may not be continuous.
$\mathcal {C}(S^1)$
are bounded, it is possible that an orbit may not converge or, even if it converges, the limit function may not be continuous.
5 Classification up to conjugacy
Since
![]() $\mathbb {R}$
is not homeomorphic to
$\mathbb {R}$
is not homeomorphic to
![]() $S^1$
, it is natural to expect that the dynamics of
$S^1$
, it is natural to expect that the dynamics of
![]() $\mathcal {J}_n$
on
$\mathcal {J}_n$
on
![]() $\mathcal {C}(\mathbb {R})$
is ‘different’ from that on
$\mathcal {C}(\mathbb {R})$
is ‘different’ from that on
![]() $\mathcal {C}(S^1)$
. This is also evident from our discussion as
$\mathcal {C}(S^1)$
. This is also evident from our discussion as
![]() $\mathcal {J}_n$
has periodic points of all periods in
$\mathcal {J}_n$
has periodic points of all periods in
![]() $\mathcal {C}(S^1)$
whereas it has no non-trivial periodic points in
$\mathcal {C}(S^1)$
whereas it has no non-trivial periodic points in
![]() $\mathcal {C}(\mathbb {R})$
for
$\mathcal {C}(\mathbb {R})$
for
![]() $n\ge 2$
. This leads to the question: Is the dynamics of
$n\ge 2$
. This leads to the question: Is the dynamics of
![]() $\mathcal {J}_n$
on
$\mathcal {J}_n$
on
![]() $\mathcal {C}(X)$
identical to that on
$\mathcal {C}(X)$
identical to that on
![]() $\mathcal {C}(Y)$
whenever X is homeomorphic to Y? We investigate this question in this section in locally compact spaces.
$\mathcal {C}(Y)$
whenever X is homeomorphic to Y? We investigate this question in this section in locally compact spaces.
Let
![]() $(X,f)$
and
$(X,f)$
and
![]() $(Y, g)$
be two discrete semi-dynamical systems. As defined in [Reference Holmgren10], we say that
$(Y, g)$
be two discrete semi-dynamical systems. As defined in [Reference Holmgren10], we say that
![]() $(X,f)$
is topologically conjugate (or simply conjugate) to
$(X,f)$
is topologically conjugate (or simply conjugate) to
![]() $(Y,g)$
if there exists a homeomorphism
$(Y,g)$
if there exists a homeomorphism
![]() $h:X\to Y$
such that
$h:X\to Y$
such that
![]() $h\circ f=g\circ h$
. In this case, h is called a topological conjugacy.
$h\circ f=g\circ h$
. In this case, h is called a topological conjugacy.
Theorem 10. Let X and Y be locally compact Hausdorff spaces. If X is homeomorphic to Y, then
![]() $(\mathcal {C}(X), \mathcal {J}_n)$
is conjugate to
$(\mathcal {C}(X), \mathcal {J}_n)$
is conjugate to
![]() $(\mathcal {C}(Y), \mathcal {J}_n)$
for each
$(\mathcal {C}(Y), \mathcal {J}_n)$
for each
![]() $n \in \mathbb {N}$
.
$n \in \mathbb {N}$
.
Proof. Let h be a homeomorphism of X onto Y. Define a map
![]() $\mathcal {H}:\mathcal {C}(X) \to \mathcal {C}(Y)$
as
$\mathcal {H}:\mathcal {C}(X) \to \mathcal {C}(Y)$
as
Then
![]() $\mathcal {H}$
is a well-defined bijective map. To prove the continuity of
$\mathcal {H}$
is a well-defined bijective map. To prove the continuity of
![]() $\mathcal {H}$
, first we claim that the map
$\mathcal {H}$
, first we claim that the map
![]() $\mathcal {F}:Y\times \mathcal {C}(X)\to Y$
defined by
$\mathcal {F}:Y\times \mathcal {C}(X)\to Y$
defined by
![]() $\mathcal {F}(y,f):=h\circ f\circ h^{-1}(y)$
is continuous. In fact, consider the map
$\mathcal {F}(y,f):=h\circ f\circ h^{-1}(y)$
is continuous. In fact, consider the map
![]() $\mathcal {G}:Y\times \mathcal {C}(X)\to X\times \mathcal {C}(X)$
defined by
$\mathcal {G}:Y\times \mathcal {C}(X)\to X\times \mathcal {C}(X)$
defined by
![]() $\mathcal {G}:=(h^{-1}\circ p_1, p_2)$
, where the
$\mathcal {G}:=(h^{-1}\circ p_1, p_2)$
, where the
![]() $p_i$
are the projection maps on
$p_i$
are the projection maps on
![]() $Y\times \mathcal {C}(X)$
given by
$Y\times \mathcal {C}(X)$
given by
![]() $p_1(y,f):=y$
and
$p_1(y,f):=y$
and
![]() $p_2(y,f):=f$
. Since
$p_2(y,f):=f$
. Since
![]() $h^{-1}\circ p_1$
and
$h^{-1}\circ p_1$
and
![]() $p_2$
are continuous, so is
$p_2$
are continuous, so is
![]() $\mathcal {G}$
. Also, by Lemma 2, the evaluation map
$\mathcal {G}$
. Also, by Lemma 2, the evaluation map
![]() $\mathcal {E}:X \times \mathcal {C}(X)\to X$
, defined by
$\mathcal {E}:X \times \mathcal {C}(X)\to X$
, defined by
![]() $\mathcal {E}(x,f):=f(x)$
, is continuous. Now,
$\mathcal {E}(x,f):=f(x)$
, is continuous. Now,
 $$ \begin{align*} h\circ \mathcal{E}\circ \mathcal{G}(y, f)&=h(\mathcal{E}(h^{-1}\circ p_1(y,f), p_2(y,f))) \\ &=h(\mathcal{E}(h^{-1}(y), f))\\ &=h(f(h^{-1}(y)))=\mathcal{F}(y,f) \end{align*} $$
$$ \begin{align*} h\circ \mathcal{E}\circ \mathcal{G}(y, f)&=h(\mathcal{E}(h^{-1}\circ p_1(y,f), p_2(y,f))) \\ &=h(\mathcal{E}(h^{-1}(y), f))\\ &=h(f(h^{-1}(y)))=\mathcal{F}(y,f) \end{align*} $$
for each
![]() $(y,f)\in Y\times \mathcal {C}(X)$
, implying that
$(y,f)\in Y\times \mathcal {C}(X)$
, implying that
![]() $\mathcal {F}=h\circ \mathcal {E}\circ \mathcal {G}$
. Therefore, being the composition of continuous maps h,
$\mathcal {F}=h\circ \mathcal {E}\circ \mathcal {G}$
. Therefore, being the composition of continuous maps h,
![]() $\mathcal {E}$
, and
$\mathcal {E}$
, and
![]() $\mathcal {G}$
,
$\mathcal {G}$
,
![]() $\mathcal {F}$
is continuous, and the claim is proved.
$\mathcal {F}$
is continuous, and the claim is proved.
The map
![]() $\mathcal {H}$
is actually the induced map of
$\mathcal {H}$
is actually the induced map of
![]() $\mathcal {F}$
. Therefore, since
$\mathcal {F}$
. Therefore, since
![]() $\mathcal {F}$
is continuous, by Lemma 3, we get that
$\mathcal {F}$
is continuous, by Lemma 3, we get that
![]() $\mathcal {H}$
is continuous on
$\mathcal {H}$
is continuous on
![]() $\mathcal {C}(X)$
. By a similar argument, it follows that
$\mathcal {C}(X)$
. By a similar argument, it follows that
![]() $\mathcal {H}^{-1}$
is continuous on
$\mathcal {H}^{-1}$
is continuous on
![]() $\mathcal {C}(Y)$
. Hence,
$\mathcal {C}(Y)$
. Hence,
![]() $\mathcal {H}$
is a homeomorphism of
$\mathcal {H}$
is a homeomorphism of
![]() $\mathcal {C}(X)$
onto
$\mathcal {C}(X)$
onto
![]() $\mathcal {C}(Y)$
.
$\mathcal {C}(Y)$
.
Finally, for each
![]() $f\in \mathcal {C}(X)$
, we have
$f\in \mathcal {C}(X)$
, we have
 $$ \begin{align*} \mathcal{J}_n\circ \mathcal{H}(f)=\mathcal{J}_n(h\circ f\circ h^{-1})&=(h\circ f\circ h^{-1})^n\\ &=h\circ f^n\circ h^{-1}=h\circ \mathcal{J}_n(f)\circ h^{-1}=\mathcal{H}\circ \mathcal{J}_n(f), \end{align*} $$
$$ \begin{align*} \mathcal{J}_n\circ \mathcal{H}(f)=\mathcal{J}_n(h\circ f\circ h^{-1})&=(h\circ f\circ h^{-1})^n\\ &=h\circ f^n\circ h^{-1}=h\circ \mathcal{J}_n(f)\circ h^{-1}=\mathcal{H}\circ \mathcal{J}_n(f), \end{align*} $$
implying that
![]() $\mathcal {J}_n\circ \mathcal {H}=\mathcal {H}\circ \mathcal {J}_n$
. Therefore,
$\mathcal {J}_n\circ \mathcal {H}=\mathcal {H}\circ \mathcal {J}_n$
. Therefore,
![]() $(\mathcal {C}(X), \mathcal {J}_n)$
is conjugate to
$(\mathcal {C}(X), \mathcal {J}_n)$
is conjugate to
![]() $(\mathcal {C}(Y), \mathcal {J}_n)$
.
$(\mathcal {C}(Y), \mathcal {J}_n)$
.
In contrast to the above theorem, it is more interesting to see whether
![]() $(\mathcal {C}(X), \mathcal {J}_n)$
is still conjugate to
$(\mathcal {C}(X), \mathcal {J}_n)$
is still conjugate to
![]() $(\mathcal {C}(Y), \mathcal {J}_n)$
for some
$(\mathcal {C}(Y), \mathcal {J}_n)$
for some
![]() $n\in \mathbb {N}$
and some spaces X and Y which are not homeomorphic to each other, unless we can prove the converse of the above theorem. Concerning the converse, we need to consider the weaker converse first and ask: Does the notion
$n\in \mathbb {N}$
and some spaces X and Y which are not homeomorphic to each other, unless we can prove the converse of the above theorem. Concerning the converse, we need to consider the weaker converse first and ask: Does the notion
![]() $\mathcal {C}(X)$
is homeomorphic to
$\mathcal {C}(X)$
is homeomorphic to
![]() $\mathcal {C}(Y)$
imply that X is homeomorphic to Y? The answer is no in general because of the following counter-example.
$\mathcal {C}(Y)$
imply that X is homeomorphic to Y? The answer is no in general because of the following counter-example.
Counter-example.
![]() $\mathcal {C}([a,b])$
is homeomorphic to
$\mathcal {C}([a,b])$
is homeomorphic to
![]() $\mathcal {C}(\mathbb {R})$
, although
$\mathcal {C}(\mathbb {R})$
, although
![]() $[a,b]$
is not homeomorphic to
$[a,b]$
is not homeomorphic to
![]() $\mathbb {R}$
.
$\mathbb {R}$
.
In fact, as shown in [Reference Narici and Beckenstein22, pp. 116–122], a seminorm on a real vector space X is a map
![]() $p:X\to \mathbb {R}$
satisfying the following conditions: (i)
$p:X\to \mathbb {R}$
satisfying the following conditions: (i)
![]() $p(x)\ge 0$
for all
$p(x)\ge 0$
for all
![]() $x\in X$
; (ii)
$x\in X$
; (ii)
![]() $p(\unicode{x3bb} x)=|\unicode{x3bb} |p(x)$
for all
$p(\unicode{x3bb} x)=|\unicode{x3bb} |p(x)$
for all
![]() $\unicode{x3bb} \in \mathbb {R}$
and
$\unicode{x3bb} \in \mathbb {R}$
and
![]() $x\in X$
; (iii)
$x\in X$
; (iii)
![]() $p(x+y)\le p(x)+p(y)$
for all
$p(x+y)\le p(x)+p(y)$
for all
![]() $x,y\in X$
. A real topological vector space X along with a family
$x,y\in X$
. A real topological vector space X along with a family
![]() $\mathcal {P}$
of seminorms on it is said to be a locally convex space. As shown in [Reference Willard26, pp. 175–176], a topological space X is said to be completely metrizable if there exists a complete metric on it inducing its topology. As seen at the end of §3.2,
$\mathcal {P}$
of seminorms on it is said to be a locally convex space. As shown in [Reference Willard26, pp. 175–176], a topological space X is said to be completely metrizable if there exists a complete metric on it inducing its topology. As seen at the end of §3.2,
![]() $\mathcal {C}(\mathbb {R})$
in the the compact-open topology is metrizable with metric D defined as in equations (2.2)–(2.4), where d is the usual metric on
$\mathcal {C}(\mathbb {R})$
in the the compact-open topology is metrizable with metric D defined as in equations (2.2)–(2.4), where d is the usual metric on
![]() $\mathbb {R}$
. Also, by [Reference Conway7, Proposition 1.12, p. 145], D is complete. Hence,
$\mathbb {R}$
. Also, by [Reference Conway7, Proposition 1.12, p. 145], D is complete. Hence,
![]() $\mathcal {C}(\mathbb {R})$
is completely metrizable. Further,
$\mathcal {C}(\mathbb {R})$
is completely metrizable. Further,
![]() $\mathcal {C}(\mathbb {R})$
is locally convex because the family
$\mathcal {C}(\mathbb {R})$
is locally convex because the family
![]() $\mathcal {P}=\{\rho _j:j\in \mathbb {N}\}$
of seminorms induces the compact-open topology on it. Moreover, by of [Reference Kundu and Garg15, Theorem 5.2, p. 694],
$\mathcal {P}=\{\rho _j:j\in \mathbb {N}\}$
of seminorms induces the compact-open topology on it. Moreover, by of [Reference Kundu and Garg15, Theorem 5.2, p. 694],
![]() $\mathcal {C}(\mathbb {R})$
is separable. However,
$\mathcal {C}(\mathbb {R})$
is separable. However,
![]() ${C}([a,b], \mathbb {R})$
, the space of all continuous functions of
${C}([a,b], \mathbb {R})$
, the space of all continuous functions of
![]() $[a,b]$
into
$[a,b]$
into
![]() $\mathbb {R}$
in the uniform topology induced by the uniform metric
$\mathbb {R}$
in the uniform topology induced by the uniform metric
![]() $\rho $
, is also a completely metrizable space. Further, by using the Weierstrass polynomial approximation theorem, it follows that
$\rho $
, is also a completely metrizable space. Further, by using the Weierstrass polynomial approximation theorem, it follows that
![]() ${C}([a,b], \mathbb {R})$
is also separable. Moreover, it is locally convex, being a normed linear space. Thus, both
${C}([a,b], \mathbb {R})$
is also separable. Moreover, it is locally convex, being a normed linear space. Thus, both
![]() ${C}([a,b], \mathbb {R})$
and
${C}([a,b], \mathbb {R})$
and
![]() $\mathcal {C}(\mathbb {R})$
are infinite dimensional separable completely metrizable locally convex linear spaces. Hence, by the Anderson–Kadec theorem (cf. [Reference Bessaga and Pełczyński3, Theorem 5.2, p. 189]), which states that every infinite dimensional separable Banach space is homeomorphic to the countable product
$\mathcal {C}(\mathbb {R})$
are infinite dimensional separable completely metrizable locally convex linear spaces. Hence, by the Anderson–Kadec theorem (cf. [Reference Bessaga and Pełczyński3, Theorem 5.2, p. 189]), which states that every infinite dimensional separable Banach space is homeomorphic to the countable product
![]() $\mathbb {R}^\omega $
of
$\mathbb {R}^\omega $
of
![]() $\mathbb {R}$
with itself in the product topology, it follows that they are homeomorphic as topological spaces. Moreover, by a known result (cf. [Reference Bessaga and Pełczyński3, Theorem 6.2 p. 190]), which states that every closed convex set of non-empty interior in an infinite dimensional Banach space is homeomorphic to the whole space, we get that
$\mathbb {R}$
with itself in the product topology, it follows that they are homeomorphic as topological spaces. Moreover, by a known result (cf. [Reference Bessaga and Pełczyński3, Theorem 6.2 p. 190]), which states that every closed convex set of non-empty interior in an infinite dimensional Banach space is homeomorphic to the whole space, we get that
![]() $\mathcal {C}([a,b])$
is homeomorphic to
$\mathcal {C}([a,b])$
is homeomorphic to
![]() ${C}([a,b],\mathbb {R})$
. Therefore,
${C}([a,b],\mathbb {R})$
. Therefore,
![]() $\mathcal {C}([a,b])$
is homeomorphic to
$\mathcal {C}([a,b])$
is homeomorphic to
![]() $\mathcal {C}(\mathbb {R})$
.
$\mathcal {C}(\mathbb {R})$
.
Another concern is the question: Even if
![]() $\mathcal {C}(X)$
is homeomorphic to
$\mathcal {C}(X)$
is homeomorphic to
![]() $\mathcal {C}(Y)$
, is
$\mathcal {C}(Y)$
, is
![]() $(\mathcal {C}(X),\mathcal {J}_m)$
conjugate to
$(\mathcal {C}(X),\mathcal {J}_m)$
conjugate to
![]() $(\mathcal {C}(Y),\mathcal {J}_n)$
for different m and n? As observed from Theorem 4, the existence of decreasing involutory fixed points ensures that
$(\mathcal {C}(Y),\mathcal {J}_n)$
for different m and n? As observed from Theorem 4, the existence of decreasing involutory fixed points ensures that
![]() $\mathcal {J}_3$
is not conjugate to
$\mathcal {J}_3$
is not conjugate to
![]() $\mathcal {J}_2$
on
$\mathcal {J}_2$
on
![]() $\mathcal {C}(\mathbb {R})$
. More generally, we have the following theorem.
$\mathcal {C}(\mathbb {R})$
. More generally, we have the following theorem.
Theorem 11. Let X be a locally compact Hausdorff space such that there exists an involutory map
![]() $f_0\ne \mathrm {id}$
in
$f_0\ne \mathrm {id}$
in
![]() $\mathcal {C}(X)$
. Then,
$\mathcal {C}(X)$
. Then,
![]() $(\mathcal {C}(X), \mathcal {J}_2)$
is not conjugate to
$(\mathcal {C}(X), \mathcal {J}_2)$
is not conjugate to
![]() $(\mathcal {C}(Y), \mathcal {J}_m)$
for each locally compact Hausdorff space Y and odd positive integer m.
$(\mathcal {C}(Y), \mathcal {J}_m)$
for each locally compact Hausdorff space Y and odd positive integer m.
Proof. Suppose that
![]() $\mathcal {H}$
is a conjugacy of
$\mathcal {H}$
is a conjugacy of
![]() $(\mathcal {C}(Y),\mathcal {J}_m)$
and
$(\mathcal {C}(Y),\mathcal {J}_m)$
and
![]() $(\mathcal {C}(X),\mathcal {J}_2)$
. Then
$(\mathcal {C}(X),\mathcal {J}_2)$
. Then
![]() $\mathcal {H}:\mathcal {C}(Y)\to \mathcal {C}(X)$
is a homeomorphism such that
$\mathcal {H}:\mathcal {C}(Y)\to \mathcal {C}(X)$
is a homeomorphism such that
Let
![]() $f_1=f_0$
and
$f_1=f_0$
and
![]() $f_2=\mathrm {id}$
. Then there exist
$f_2=\mathrm {id}$
. Then there exist
![]() $g_1\ne g_2 \in \mathcal {C}(Y)$
such that
$g_1\ne g_2 \in \mathcal {C}(Y)$
such that
![]() $f_1=\mathcal {H}(g_1)$
and
$f_1=\mathcal {H}(g_1)$
and
![]() $f_2=\mathcal {H}(g_2)$
. We have
$f_2=\mathcal {H}(g_2)$
. We have
![]() $\text {id}=f_1^2=\mathcal {H}(g_1)^2=\mathcal {H}(g_1^m)$
and
$\text {id}=f_1^2=\mathcal {H}(g_1)^2=\mathcal {H}(g_1^m)$
and
![]() $\text {id}=f_2^2=\mathcal {H}(g_2)^2=\mathcal {H}(g_2^m)$
, implying that
$\text {id}=f_2^2=\mathcal {H}(g_2)^2=\mathcal {H}(g_2^m)$
, implying that
![]() $g_1^m=g_2^m$
, because
$g_1^m=g_2^m$
, because
![]() $\mathcal {H}$
is one-to-one. Since m is odd,
$\mathcal {H}$
is one-to-one. Since m is odd,
![]() $f_1$
is a fixed point for
$f_1$
is a fixed point for
![]() $\mathcal {J}_m$
, implying that
$\mathcal {J}_m$
, implying that
![]() $g_1$
is a fixed point for
$g_1$
is a fixed point for
![]() $\mathcal {J}_2$
, that is,
$\mathcal {J}_2$
, that is,
![]() $g_1^2=g_1$
and therefore
$g_1^2=g_1$
and therefore
![]() $g_1^m=g_1$
. Similarly, since
$g_1^m=g_1$
. Similarly, since
![]() $f_2$
is a fixed point for
$f_2$
is a fixed point for
![]() $\mathcal {J}_m$
, it follows that
$\mathcal {J}_m$
, it follows that
![]() $g_2$
is a fixed point for
$g_2$
is a fixed point for
![]() $\mathcal {J}_2$
, that is,
$\mathcal {J}_2$
, that is,
![]() $g_2^2=g_2$
, and therefore
$g_2^2=g_2$
, and therefore
![]() $g_2^m=g_2$
. Hence, we have
$g_2^m=g_2$
. Hence, we have
![]() $g_1=g_2$
, which is a contradiction. So
$g_1=g_2$
, which is a contradiction. So
![]() $(\mathcal {C}(Y), \mathcal {J}_m)$
is not conjugate to
$(\mathcal {C}(Y), \mathcal {J}_m)$
is not conjugate to
![]() $(\mathcal {C}(X), \mathcal {J}_2)$
and the result follows.
$(\mathcal {C}(X), \mathcal {J}_2)$
and the result follows.
6 Remarks and questions
The iteration operator
![]() $\mathcal {J}_1$
has no non-trivial periodic points in both
$\mathcal {J}_1$
has no non-trivial periodic points in both
![]() $\mathcal {C}(\mathbb {R})$
and
$\mathcal {C}(\mathbb {R})$
and
![]() $\mathcal {C}(S^1)$
. Also, unlike
$\mathcal {C}(S^1)$
. Also, unlike
![]() $\mathcal {C}(\mathbb {R})$
, where there are no non-trivial periodic points as seen in Theorem 5,
$\mathcal {C}(\mathbb {R})$
, where there are no non-trivial periodic points as seen in Theorem 5,
![]() $\mathcal {J}_n$
has periodic points of all periods in
$\mathcal {J}_n$
has periodic points of all periods in
![]() $\mathcal {C}(S^1)$
for
$\mathcal {C}(S^1)$
for
![]() $n\ge 2$
(see Example 3). Further, we have the following result.
$n\ge 2$
(see Example 3). Further, we have the following result.
Proposition. The Sharkovskii theorem, that is, the existence of
![]() $3$
-periodic points implies that of k-periodic points for all
$3$
-periodic points implies that of k-periodic points for all
![]() $k\ge 1$
, is valid in both the systems
$k\ge 1$
, is valid in both the systems
![]() $(\mathcal {C}(\mathbb {R}), \mathcal {J}_n)$
and
$(\mathcal {C}(\mathbb {R}), \mathcal {J}_n)$
and
![]() $(\mathcal {C}(S^1), \mathcal {J}_n)$
for all
$(\mathcal {C}(S^1), \mathcal {J}_n)$
for all
![]() $n\ge 1$
.
$n\ge 1$
.
In fact, in the cases of
![]() $(\mathcal {C}(\mathbb {R}), \mathcal {J}_n)$
with
$(\mathcal {C}(\mathbb {R}), \mathcal {J}_n)$
with
![]() $n\ge 1$
and
$n\ge 1$
and
![]() $(\mathcal {C}(S^1), \mathcal {J}_1)$
, the result follows vacuously since there are no
$(\mathcal {C}(S^1), \mathcal {J}_1)$
, the result follows vacuously since there are no
![]() $3$
-periodic points. However, in the case of
$3$
-periodic points. However, in the case of
![]() $(\mathcal {C}(S^1), \mathcal {J}_n)$
with
$(\mathcal {C}(S^1), \mathcal {J}_n)$
with
![]() $n\ge 2$
, there are k-periodic points for all
$n\ge 2$
, there are k-periodic points for all
![]() $k\ge 1$
as seen from Example 3. Observe that this proposition makes a contrast with the Sharkovskii theorem on the underlying spaces
$k\ge 1$
as seen from Example 3. Observe that this proposition makes a contrast with the Sharkovskii theorem on the underlying spaces
![]() $\mathbb {R}$
and
$\mathbb {R}$
and
![]() $S^1$
because the Sharkovskii theorem holds valid on
$S^1$
because the Sharkovskii theorem holds valid on
![]() $\mathbb {R}$
but not on
$\mathbb {R}$
but not on
![]() $S^1$
(see, for example, the rotation map
$S^1$
(see, for example, the rotation map
![]() $R_{{2\pi }/{3}}$
on
$R_{{2\pi }/{3}}$
on
![]() $S^1$
defined as in Example 3).
$S^1$
defined as in Example 3).
Additionally, from Theorem 10, we can conclude that it suffices to discuss the dynamics of
![]() $\mathcal {J}_n$
on
$\mathcal {J}_n$
on
![]() $\mathcal {C}(X)$
for X to be a representative of the equivalence class
$\mathcal {C}(X)$
for X to be a representative of the equivalence class
![]() $[X]$
under the homeomorphism equivalence relation. In view of this observation, it follows that dynamics of
$[X]$
under the homeomorphism equivalence relation. In view of this observation, it follows that dynamics of
![]() $\mathcal {J}_n$
on
$\mathcal {J}_n$
on
![]() $\mathcal {C}(X)$
is identical to that on:
$\mathcal {C}(X)$
is identical to that on:
-
(i)
 $\mathcal {C}(\mathbb {R})$
(respectively
$\mathcal {C}(\mathbb {R})$
(respectively
 $\mathcal {C}([a,b])$
) whenever X is, for example, a curve in
$\mathcal {C}([a,b])$
) whenever X is, for example, a curve in
 $\mathbb {C}$
homeomorphic to
$\mathbb {C}$
homeomorphic to
 $\mathbb {R}$
(respectively
$\mathbb {R}$
(respectively
 $[a,b]$
);
$[a,b]$
); -
(ii)
 $\mathcal {C}(S^1)$
whenever X is, for example, a simple closed curve in
$\mathcal {C}(S^1)$
whenever X is, for example, a simple closed curve in
 $\mathbb {C}$
, or the real projective line
$\mathbb {C}$
, or the real projective line
 $\mathbb {RP}^1$
.
$\mathbb {RP}^1$
.
Moreover, by the Hahn–Mazurkiewicz theorem [Reference Willard26], a Hausdorff topological space X is a continuous image of
![]() $[a,b]$
or
$[a,b]$
or
![]() $S^1$
if and only if it is a Peano space (that is, a compact, connected, locally connected, metric space). Therefore, the equivalence class
$S^1$
if and only if it is a Peano space (that is, a compact, connected, locally connected, metric space). Therefore, the equivalence class
![]() $[[a,b]]$
of
$[[a,b]]$
of
![]() $[a,b]$
(respectively
$[a,b]$
(respectively
![]() $[S^1]$
of
$[S^1]$
of
![]() $S^1$
) also contains subspaces of some ‘complicated’ spaces in the Euclidean plane
$S^1$
) also contains subspaces of some ‘complicated’ spaces in the Euclidean plane
![]() $\mathbb {R}^2$
like the space filling curves—Peano curve, Hilbert curve, Sierpiński curve (respectively like Sierpiński triangle).
$\mathbb {R}^2$
like the space filling curves—Peano curve, Hilbert curve, Sierpiński curve (respectively like Sierpiński triangle).
Finally, we conclude the paper with some problems for future discussion. Since any non-constant map f in
![]() $\mathcal {C}_{\mathrm {id}}(\mathbb {R})$
(respectively
$\mathcal {C}_{\mathrm {id}}(\mathbb {R})$
(respectively
![]() $\mathcal {C}_{\mathrm {id}}(S^1)$
) has a unique choice for
$\mathcal {C}_{\mathrm {id}}(S^1)$
) has a unique choice for
![]() $f|_{R(f)}$
, namely
$f|_{R(f)}$
, namely
![]() $\mathrm {id}$
, we were indeed able to use the definition of stability to prove the instability of such maps in Theorem 8 (respectively Theorem 9). However, if f lies in
$\mathrm {id}$
, we were indeed able to use the definition of stability to prove the instability of such maps in Theorem 8 (respectively Theorem 9). However, if f lies in
![]() $\mathcal {C}_{\mathrm {inv}}(S^1)$
(consisting of all continuous self-maps of
$\mathcal {C}_{\mathrm {inv}}(S^1)$
(consisting of all continuous self-maps of
![]() $S^1$
which are orientation-reversing involutions on their range), then
$S^1$
which are orientation-reversing involutions on their range), then
![]() $f|_{R(f)}$
has uncountably many choices and therefore the case-wise approach used in the proof of the above theorem is impractical. Thus, the problem of stability of fixed points of
$f|_{R(f)}$
has uncountably many choices and therefore the case-wise approach used in the proof of the above theorem is impractical. Thus, the problem of stability of fixed points of
![]() $\mathcal {J}_n$
, which are in
$\mathcal {J}_n$
, which are in
![]() $\mathcal {C}_{\mathrm {inv}}(S^1)$
, is highly non-trivial. For the same reason, the problem of stability of fixed points of
$\mathcal {C}_{\mathrm {inv}}(S^1)$
, is highly non-trivial. For the same reason, the problem of stability of fixed points of
![]() $\mathcal {J}_n$
in
$\mathcal {J}_n$
in
![]() $\mathcal {C}_{\mathrm {inv}}(\mathbb {R})$
is also highly non-trivial. Additionally, although
$\mathcal {C}_{\mathrm {inv}}(\mathbb {R})$
is also highly non-trivial. Additionally, although
![]() $\mathcal {J}_n$
does not have a non-trivial periodic point in
$\mathcal {J}_n$
does not have a non-trivial periodic point in
![]() $\mathcal {C}(\mathbb {R})$
by Theorem 5, the problem of stability of periodic points of
$\mathcal {C}(\mathbb {R})$
by Theorem 5, the problem of stability of periodic points of
![]() $\mathcal {J}_n$
in
$\mathcal {J}_n$
in
![]() $\mathcal {C}(S^1)$
is also difficult. Further, we remind that we did not conclude the discussion in Theorem 11 for all pairs n and m, which is interesting to consider. We observed through the counter-example given in §5 that a weaker converse of Theorem 10 is not true in general. However, it is interesting to investigate if the actual converse of Theorem 10 is true, that is, does
$\mathcal {C}(S^1)$
is also difficult. Further, we remind that we did not conclude the discussion in Theorem 11 for all pairs n and m, which is interesting to consider. We observed through the counter-example given in §5 that a weaker converse of Theorem 10 is not true in general. However, it is interesting to investigate if the actual converse of Theorem 10 is true, that is, does
![]() $(\mathcal {C}(X), \mathcal {J}_n)$
is conjugate to
$(\mathcal {C}(X), \mathcal {J}_n)$
is conjugate to
![]() $(\mathcal {C}(Y), \mathcal {J}_n)$
imply that X is homeomorphic to Y?
$(\mathcal {C}(Y), \mathcal {J}_n)$
imply that X is homeomorphic to Y?
Acknowledgements
Chaitanya Gopalakrishna is supported by the National Institute of Technology Karnataka Surathkal through Senior Research Fellowship, the Indian Statistical Institute Bangalore through the J. C. Bose Fellowship of Prof. B. V. Rajarama Bhat, and the National Board for Higher Mathematics, India through No. 0204/3/2021/R&D-II/7389. Murugan Veerapazham is supported by SERB, DST, Government of India, through ECR/2017/000765. Weinian Zhang is supported by NSFC Nos. 11831012, 12171336, and 11821001.