Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-28T03:22:50.388Z Has data issue: false hasContentIssue false
  • English
  • Français

Dynamics induced on the ends of non-compact manifold

Published online by Cambridge University Press:  19 September 2008

Steve Alpern  and
V. S. Prasad
Steve Alpern
Affiliation:
Department of Mathematics, London School of Economics, University of London, London WC2A 2AE, England
V. S. Prasad
Affiliation:
York University, North York, Canada M3J 1P3
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let ℋ denote the group of homeomorphisms of a σ-compact manifold M which preserve a locally positive non-atomic measure μ. Such a manifold can be compactified by adjoining ideal points called ‘ends’, collectively denoted by E. Every homeomorphism h in ℋ induces a measure preserving system (E, 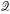, μ*, h*) where 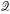is the algebra of clopen subsets of E, μ* is a 0-∞ measure induced on E by μ, and h*: E → E is a μ*-preserving homeomorphism. For any induced homeomorphism σ = f*, where f belongs to ℋ, define ℋσ = {h ∈ ℋ: h* = σ}. We prove that ergodicity is generic in ℋσ for the compact-open topology if and only if (E, 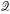, μ*, σ) is incompressible and ergodic. Furthermore ℋσ contains an ergodic homeomorphism if and only if (E, 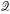, μ*, σ) is incompressible. Since the identity on M induces the identity on E, which is incompressible, our results establish that every manifold (M, μ) supports an ergodic μ-preserving homeomorphism.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 8 , Issue 1 , March 1988 , pp. 1 - 15
Copyright
Copyright © Cambridge University Press 1988

References

REFERENCES

[Al]Alpern, S.. Approximation to and by measure preserving homeomorphisms. J. London Math. Soc. 18 (1978), 305–315.CrossRefGoogle Scholar
[A2]Alpern, S.. Generic properties of measure preserving homeomorphisms. Ergodic Theory, Proceedings Oberwolfach 1978, Springer Lecture Notes in Math. 729 (1979), 16–27.CrossRefGoogle Scholar
[A3]Alpern, S.. Return times and conjugates of an antiperiodic transformation. Ergod. Th. & Dynam. Sys. 1 (1981), 135–143.CrossRefGoogle Scholar
[A4]Alpern, S.. Nonstable ergodic homeomorphisms of ℝ4. Indiana U. Math. J. 32 (1983), 187–191.CrossRefGoogle Scholar
[A–P]Alpern, S. & Prasad, V. S.. End behaviour and ergodicity for homeomorphisms of manifolds with finitely many ends. Canadian J. Math. 39 (1987), 473–492.CrossRefGoogle Scholar
[B–E]Berlanga, R. & Epstein, D.. Measures on sigma compact manifolds and their equivalences under homeomorphisms. J. London Math. Soc. 27 (1983), 63–74.CrossRefGoogle Scholar
[C–K]Choksi, J. & Kakutani, S.. Residuality of ergodic measurable transformations and of ergodic transformations which preserve an infinite measure. Indiana U. Math. J. 28 (1979), 453–459.CrossRefGoogle Scholar
[F]Fathi, A.. The structure of homeomorphisms preserving a good measure. Ann. Scient. Ec. Norm. Sup. 13 (1980), 45–93.CrossRefGoogle Scholar
[K–St]Katok, A. & Stepin, A.. Metric properties of measure preserving homeomorphisms. Uspekhi Math. Nauk 25 (1970), 193–222;Google Scholar
translated in Russian Math. Surveys 25 (1970), 191–220.CrossRefGoogle Scholar
[K–S]Kirby, R. & Siebenmann, L.. Foundational Essays on Topological Manifolds, Smoothings and Triangulations. Annals of Math. Studies No. 88, Princeton Univ. Press, 1977.CrossRefGoogle Scholar
[O]Oxtoby, J.. Approximation by measure preserving homeomorphisms. Recent Advances in Topological Dynamics, Springer Lecture Notes in Math. 318 (1973), 206–217.CrossRefGoogle Scholar
[O–U]Oxtoby, J. & Ulam, S.. Measure preserving homeomorphisms and metrical transitivity. Ann. of Math. 42 (1941), 874–920.CrossRefGoogle Scholar
[P]Prasad, V. S.. Ergodic measure preserving homeomorphisms of ℝn, Indiana U. Math. J. 28 (1979), 859–867.CrossRefGoogle Scholar
[Q]Quinn, F.. Ends of maps, III. J. Diff. Geom. 17 (1982) 503–521.Google Scholar
[W]White, H. E. Jr, The approximation of one-one measurable transformations by measure preserving homeomorphisms. Proc. Amer. Math. Soc. 44 (1974), 391–394.CrossRefGoogle Scholar