Hostname: page-component-6bf8c574d5-t27h7 Total loading time: 0 Render date: 2025-02-17T00:42:30.882Z Has data issue: false hasContentIssue false
  • English
  • Français

Dynamics and eigenvalues in dimension zero

Part of: Homology and cohomology theories Low-dimensional dynamical systems Topological dynamics

Published online by Cambridge University Press:  04 January 2019

LUIS HERNÁNDEZ-CORBATO Open the ORCID record for LUIS HERNÁNDEZ-CORBATO [Opens in a new window] ,
DAVID JESÚS NIEVES-RIVERA Open the ORCID record for DAVID JESÚS NIEVES-RIVERA [Opens in a new window] ,
FRANCISCO R. RUIZ DEL PORTAL Open the ORCID record for FRANCISCO R. RUIZ DEL PORTAL [Opens in a new window]  and
JAIME J. SÁNCHEZ-GABITES Open the ORCID record for JAIME J. SÁNCHEZ-GABITES [Opens in a new window]
LUIS HERNÁNDEZ-CORBATO
Affiliation:
Departamento de Matemática Aplicada a las TIC, Universidad Politécnica de Madrid, 28031Madrid, Spain email [email protected]
DAVID JESÚS NIEVES-RIVERA
Affiliation:
Departamento de Álgebra, Geometría y Topología, Universidad Complutense de Madrid, Plaza de Ciencias 3, 28040Madrid, Spain email [email protected], [email protected]
FRANCISCO R. RUIZ DEL PORTAL
Affiliation:
Departamento de Álgebra, Geometría y Topología, Universidad Complutense de Madrid, Plaza de Ciencias 3, 28040Madrid, Spain email [email protected], [email protected]
JAIME J. SÁNCHEZ-GABITES
Affiliation:
Departamento de Análisis Económico (Métodos cuantitativos), Facultad de Ciencias Económicas y Empresariales, Universidad Autónoma de Madrid, 28049Madrid, Spain email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 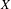$X$ be a compact, metric and totally disconnected space and let 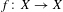$f:X\rightarrow X$ be a continuous map. We relate the eigenvalues of 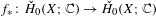$f_{\ast }:\check{H}_{0}(X;\mathbb{C})\rightarrow \check{H}_{0}(X;\mathbb{C})$ to dynamical properties of 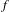$f$, roughly showing that if the dynamics is complicated then every complex number of modulus different from 0, 1 is an eigenvalue. This stands in contrast with a classical inequality of Manning that bounds the entropy of 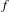$f$ below by the spectral radius of 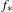$f_{\ast }$.

Keywords

Čech homologyeigenvaluesadding machinesentropy

MSC classification

Primary: 37B40: Topological entropy 37E99: None of the above, but in this section
Secondary: 37B10: Symbolic dynamics 55N05: Čech types
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 40 , Issue 9 , September 2020 , pp. 2434 - 2452
Check for updates
Copyright
© Cambridge University Press, 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Buescu, J., Kulczycki, M. and Stewart, I.. Liapunov stability and adding machines revisited. Dyn. Syst. 21 (2006), 379–384.10.1080/14689360600649815Google Scholar
Buescu, J. and Stewart, I.. Liapunov stability and adding machines. Ergod. Th. & Dynam. Sys. 15 (1995), 271–290.Google Scholar
Hatcher, A.. Algebraic Topology. Cambridge University Press, Cambridge, 2002.Google Scholar
Hurewicz, W. and Wallman, H.. Dimension Theory (Princeton Mathematical Series, 4). Princeton University Press, Princeton, NJ, 1941.Google Scholar
Manning, A.. Topological entropy and the first homology group. Dynamical Systems—Warwick 1974 (Proc. Symp. Appl. Topology and Dynamical Systems, University of Warwick, Coventry, 1973/1974) (Lecture Notes in Mathematics, 468). Springer, Berlin, 1975, pp. 185–190.Google Scholar
Spanier, E. H.. Cohomology theory for general spaces. Ann. of Math. (2) 49 (1948), 407–427.10.2307/1969289Google Scholar
Spanier, E. H.. Algebraic Topology. McGraw-Hill, New York, 1966.Google Scholar