Article contents
Dynamical simplices and Fraïssé theory
Published online by Cambridge University Press: 13 March 2018
Abstract
We simplify a criterion (due to Ibarlucía and the author) which characterizes dynamical simplices, that is, sets 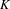 $K$ of probability measures on a Cantor space
$K$ of probability measures on a Cantor space 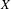 $X$ for which there exists a minimal homeomorphism of
$X$ for which there exists a minimal homeomorphism of 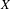 $X$ whose set of invariant measures coincides with
$X$ whose set of invariant measures coincides with 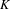 $K$. We then point out that this criterion is related to Fraïssé theory, and use that connection to provide a new proof of Downarowicz’ theorem stating that any non-empty metrizable Choquet simplex is affinely homeomorphic to a dynamical simplex. The construction enables us to prove that there exist minimal homeomorphisms of a Cantor space which are speedup equivalent but not orbit equivalent, answering a question of Ash.
$K$. We then point out that this criterion is related to Fraïssé theory, and use that connection to provide a new proof of Downarowicz’ theorem stating that any non-empty metrizable Choquet simplex is affinely homeomorphic to a dynamical simplex. The construction enables us to prove that there exist minimal homeomorphisms of a Cantor space which are speedup equivalent but not orbit equivalent, answering a question of Ash.
- Type
- Original Article
- Information
- Copyright
- © Cambridge University Press, 2018
References
- 5
- Cited by


