Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-25T21:39:03.305Z Has data issue: false hasContentIssue false
  • English
  • Français

Dynamical sets whose union with infinity is connected

Published online by Cambridge University Press:  10 August 2018

DAVID J. SIXSMITH Open the ORCID record for DAVID J. SIXSMITH [Opens in a new window]
DAVID J. SIXSMITH*
Affiliation:
Department of Mathematical Sciences, University of Liverpool, Liverpool L69 7ZL, UK email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Suppose that 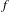$f$ is a transcendental entire function. In 2011, Rippon and Stallard showed that the union of the escaping set with infinity is always connected. In this paper we consider the related question of whether the union with infinity of the bounded orbit set, or the bungee set, can also be connected. We give sufficient conditions for these sets to be connected and an example of a transcendental entire function for which all three sets are simultaneously connected. This function lies, in fact, in the Speiser class.

It is known that for many transcendental entire functions the escaping set has a topological structure known as a spider’s web. We use our results to give a large class of functions in the Eremenko–Lyubich class for which the escaping set is not a spider’s web. Finally, we give a novel topological criterion for certain sets to be a spider’s web.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 40 , Issue 3 , March 2020 , pp. 789 - 798
Copyright
© Cambridge University Press, 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abramowitz, M. and Stegun, I. A. (Eds). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. National Bureau of Standards, Gaithersburg, MA, 1972.Google Scholar
Benini, L. and Rempe-Gillen, A.. A landing theorem for entire functions with bounded post-singular sets. Preprint, 2017, arXiv:1711.10780v2.Google Scholar
Bergweiler, W.. Iteration of meromorphic functions. Bull. Amer. Math. Soc. (N.S.) 29(2) (1993), 151–188.Google Scholar
Bergweiler, W.. On the set where the iterates of an entire function are bounded. Proc. Amer. Math. Soc. 140(3) (2012), 847–853.Google Scholar
Bergweiler, W. and Hinkkanen, A.. On semiconjugation of entire functions. Math. Proc. Cambridge Philos. Soc. 126(3) (1999), 565–574.Google Scholar
Bishop, C. J.. Constructing entire functions by quasiconformal folding. Acta Math. 214(1) (2015), 1–60.Google Scholar
Barański, K., Karpińska, B. and Zdunik, A.. Hyperbolic dimension of Julia sets of meromorphic maps with logarithmic tracts. Int. Math. Res. Not. IMRN 2009(4) (2009), 615–624.Google Scholar
Christensen, J. P. R. and Fischer, P.. Ergodic invariant probability measures and entire functions. Acta Math. Hungar. 73(3) (1996), 213–218.Google Scholar
NIST Digital Library of Mathematical Functions. http://dlmf.nist.gov/, Release 1.0.16 of 2017-09-18. Eds. F. W. J. Olver, A. B. Olde Daalhuis, D. W. Lozier, B. I. Schneider, R. F. Boisvert, C. W. Clark, B. R. Miller and B. V. Saunders.Google Scholar
Eremenko, A. E. and Lyubich, M. Yu.. Examples of entire functions with pathological dynamics. J. Lond. Math. Soc. (2) 36(3) (1987), 458–468.Google Scholar
Eremenko, A. E. and Lyubich, M. Yu.. Dynamical properties of some classes of entire functions. Ann. Inst. Fourier (Grenoble) 42(4) (1992), 989–1020.Google Scholar
Eremenko, A. E.. On the iteration of entire functions. Dynamical Systems and Ergodic Theory (Warsaw 1986) (Banach Center Publications, 23) . PWN, Warsaw, 1989, pp. 339–345.Google Scholar
Evdoridou, V. and Rempe-Gillen, L.. Non-escaping endpoints do not explode. Bull. Lond. Math. Soc., to appear, Preprint, 2017, arXiv:1707.01843v1.Google Scholar
Evdoridou, V.. Fatou’s web. Proc. Amer. Math. Soc. 144(12) (2016), 5227–5240.Google Scholar
Kisaka, M.. On the connectivity of Julia sets of transcendental entire functions. Ergod. Th. & Dynam. Sys. 18(1) (1998), 189–205.Google Scholar
Lazebnik, K.. Several constructions in the Eremenko-Lyubich class. J. Math. Anal. Appl. 448(1) (2017), 611–632.Google Scholar
Osborne, J. W., Rippon, P. J. and Stallard, G. M.. Connectedness properties of the set where the iterates of an entire function are unbounded. Ergod. Th. & Dynam. Sys. 37(4) (2017), 1291–1307.Google Scholar
Osborne, J. W. and Sixsmith, D. J.. On the set where the iterates of an entire function are neither escaping nor bounded. Ann. Acad. Sci. Fenn. Math. 41(2) (2016), 561–578.Google Scholar
Osborne, J. W.. Connectedness properties of the set where the iterates of an entire function are bounded. Math. Proc. Cambridge Philos. Soc. 155(3) (2013), 391–410.Google Scholar
Rempe, L.. Hyperbolic dimension and radial Julia sets of transcendental functions. Proc. Amer. Math. Soc. 137(4) (2009), 1411–1420.Google Scholar
Rottenfusser, G., Rückert, J., Rempe, L. and Schleicher, D.. Dynamic rays of bounded-type entire functions. Ann. of Math. (2) 173(1) (2011), 77–125.Google Scholar
Rippon, P. J. and Stallard, G. M.. Boundaries of escaping Fatou components. Proc. Amer. Math. Soc. 139(8) (2011), 2807–2820.Google Scholar
Rippon, P. J. and Stallard, G. M.. Fast escaping points of entire functions. Proc. Lond. Math. Soc. (3) 105(4) (2012), 787–820.Google Scholar
Sixsmith, D. J.. Entire functions for which the escaping set is a spider’s web. Math. Proc. Cambridge Philos. Soc. 151(3) (2011), 551–571.Google Scholar
Sixsmith, D. J.. Maximally and non-maximally fast escaping points of transcendental entire functions. Math. Proc. Cambridge Philos. Soc. 158(2) (2015), 365–383.Google Scholar
Stallard, G. M.. The Hausdorff dimension of Julia sets of meromorphic functions. J. Lond. Math. Soc. (2) 49(2) (1994), 281–295.Google Scholar