Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-26T00:35:06.374Z Has data issue: false hasContentIssue false
  • English
  • Français

Dynamical semigroups commuting with compact abelian actions

Published online by Cambridge University Press:  19 September 2008

Ola Bratteli  and
David E. Evans
Ola Bratteli
Affiliation:
Institute of Mathematics, University of Trondheim, 7034 Trondheim – NTH, Norway
David E. Evans
Affiliation:
Mathematics Institute, University of Warwick, Coventry, CVA 7AL, England
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

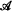Let be a C*-algebra and τ:G → Aut 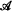a compact abelian action such that the fixed point algebra 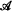τ is simple. Denote by 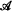F the *-subalgebra of G-finite elements. Let H: 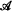F → 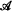be a *-operator commuting with τ such that 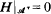and the matrix inequality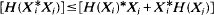

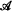holds for all finite sequences X1, …, Xn in F. Then H is closable, and the closure 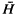is the generator of a strongly continuous semigroup {exp (−t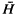): t ≥ 0} of completely positive contractions. Furthermore, there exists a convolution semigroup {μt: t ≥ 0} of probability measures on G such that

.

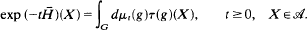This result has various extensions and refinements.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 3 , Issue 2 , June 1983 , pp. 187 - 217
Copyright
Copyright © Cambridge University Press 1983

References

REFERENCES

[1]Accardi, L. & Cecchini, C.. Conditional expectations in von Neumann algebras and a theorem of Takesaki. J. Func. Anal. 45 (1982), 245–273.CrossRefGoogle Scholar
[2]Araki, H., Haag, R., Kastler, D. & Takesaki, M.. Extensions of KMS states and chemical potential. Commun. math. Phys. 53 (1977), 97–134.CrossRefGoogle Scholar
[3]Arveson, W. B.. Subalgebras of C*-algebras. Acta Math. 123 (1969), 141–224.CrossRefGoogle Scholar
[4]Baaj, S.. Multiplicateurs non Bornés. Paris preprint (1981).Google Scholar
[5]Berg, C. & Forst, G.. Potential Theory on Locally Compact Abelian Groups. Springer-Verlag: Berlin-Heidelberg-New York, 1975.CrossRefGoogle Scholar
[6]Bratteli, O. & Jørgensen, P. E. T.. Unbounded derivations tangential to compact groups of automorphisms. J. Func. Anal. 48 (1982), 107–133.CrossRefGoogle Scholar
[7]Bratteli, O. & Robinson, D. W.. Operator Algebras and Quantum Statistical Mechanics I. Springer-Verlag: New York-Heidelberg-Berlin, 1979.CrossRefGoogle Scholar
[8]Bratteli, O. & Robinson, D. W.. Positive C 0-semigroups on C*-algebras. Math. Scand. 49 (1981), 259–274.CrossRefGoogle Scholar
[9]Bratteli, O., Elliott, G. A. & Jørgensen, P. E. T.. Decomposition of unbounded derivations into invariant and approximately inner parts. Warwick preprint, (1982).Google Scholar
[10]Brown, L. G.. Stable isomorphism of hereditary subalgebras of C*-algebras. Pacific J. Math. 71 (1977), 335–348.CrossRefGoogle Scholar
[11]Christensen, E. & Evans, D. E.. Cohomology of operator algebras and quantum dynamical semigroups. J. London Math. Soc. (2) 20 (1978), 358–368.Google Scholar
[12]Cuntz, J.. Simple C*-algebras generated by isometries. Commun. math. Phys. 57 (1977), 173–185.CrossRefGoogle Scholar
[13]Davies, E. B.. Some contraction semigroups in quantum probability. Z. Wahrscheinlichkeitstheorie verw. Geb. 23 (1972), 261–273.CrossRefGoogle Scholar
[14]Evans, D. E.. Irreducible quantum dynamical semigroups. Commun. math. Phys. 54 (1977), 293–297.CrossRefGoogle Scholar
[15]Evans, D. E.. Completely positive quasi-free maps on the CAR algebra. Commun. math. Phys. 70 (1979), 53–68.CrossRefGoogle Scholar
[16]Evans, D. E. & Lewis, J. T.. Dilations of irreversible evolutions in algebraic quantum theory. Comm. Dublin Inst. Adv. Studies, Ser. A 24 (1977).Google Scholar
[17]Goodman, F. & jørgensen, P. E. T.. Unbounded derivations commuting with compact group actions. Commun. math. Phys. 82 (1981), 399–405.CrossRefGoogle Scholar
[18]Goodman, F. & Wasserman, A.. Unbounded derivations commuting with compact group actions II. J. Fund. Anal. To appear.Google Scholar
[19]Gorini, V., Kossakowski, A. & Sudarshan, E. C. G.. Completely positive dynamical semigroups on N-level systems. J. Math. Phys. 17 (1976), 821–825.CrossRefGoogle Scholar
[20]Ikunishi, A.. Derivations in C*-algebras commuting with compact actions. Commun. math. Phys. To appear.Google Scholar
[21]Jørgensen, P. E. T.. Compact symmetry groups and generators for sub-markovian semigroups. Z. Wahrscheinlichkeitstheorie verw. Greb. To appear.Google Scholar
[22]Kishimoto, A. & Robinson, D. W.. On unbounded derivations commuting with a compact group of *-automorphisms. Commun. Math. Phys. To appear.Google Scholar
[23]Kishimoto, A. & Takai, H.. Some remarks on C*-dynamical systems with a compact abelian group. Publ. R.I.M.S. Kyoto Univ. 14 (1978), 383–397.CrossRefGoogle Scholar
[24]Lindblad, G.. On the generators of quantum dynamical semigroups. Commun. math. Phys. 48 (1976), 119–130.CrossRefGoogle Scholar
[25]Parthasarathy, K. R. & Schmidt, K.. Positive Definite Kernels, Continuous Tensor Products, and Central Limit Theorems of Probability Theory. Springer Lecture Notes No. 272, Springer-Verlag: Berlin-Heidelberg-New York, 1972.CrossRefGoogle Scholar
[26]Pedersen, G. K.. C*-algebras and their automorphism groups. Academic Press: London-New York-San Francisco, 1979.Google Scholar
[27]Peligrad, C.. Derivations of C*-algebras which are invariant under an automorphism group I, OT series vol. 2, Birkhäuser Verlag (1981) II, Bucuresti preprint 107 (1981).Google Scholar
[28]Powers, R. T. & Price, G.. Derivations commuting with S(∞). Commun. math. Phys. 84 (1982), 439–447.CrossRefGoogle Scholar
[29]Robinson, D. W.. Strongly positive semigroups and faithful invariant states. Commun. math. Phys. 85 (1982), 129–142.CrossRefGoogle Scholar
[30]Segal, I. E.. A non-commutative version of abstract integration. Ann. Math. 57 (1953), 401–457.CrossRefGoogle Scholar
[31]Stone, M. H.. On unbounded operators in Hilbert space. J. Indian. Math. Soc. 15 (1951), 155–192.Google Scholar
[32]Takesaki, M.. Theory of Operator Algebras, I. Springer-Verlag: New York-Heidelberg-Berlin, 1979.CrossRefGoogle Scholar
[33]Watanabe, S.. Asymptotic behaviour and eigenvalues of dynamical semigroups on operator algebras. Niigata preprint.Google Scholar