Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-12-01T02:54:38.276Z Has data issue: false hasContentIssue false
  • English
  • Français

Dynamical properties of some adic systems with arbitrary orderings

Published online by Cambridge University Press:  08 March 2016

SARAH FRICK ,
KARL PETERSEN  and
SANDI SHIELDS
SARAH FRICK
Affiliation:
Department of Mathematics, Furman University, Greenville, SC 29613, USA email [email protected]
KARL PETERSEN
Affiliation:
Department of Mathematics, CB 3250, Phillips Hall, University of North Carolina, Chapel Hill, NC 27599, USA email [email protected]
SANDI SHIELDS
Affiliation:
College of Charleston, 66 George St., Charleston, SC 29424-0001, USA email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider arbitrary orderings of the edges entering each vertex of the (downward directed) Pascal graph. Each ordering determines an adic (Bratteli–Vershik) system, with a transformation that is defined on most of the space of infinite paths that begin at the root. We prove that for every ordering the coding of orbits according to the partition of the path space determined by the first three edges is essentially faithful, meaning that it is one-to-one on a set of paths that has full measure for every fully supported invariant probability measure. We also show that for every 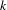$k$ the subshift that arises from coding orbits according to the first 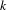$k$ edges is topologically weakly mixing. We give a necessary and sufficient condition for any adic system to be topologically conjugate to an odometer and use this condition to determine the probability that a random order on a fixed diagram, or a diagram constructed at random in some way, is topologically conjugate to an odometer. We also show that the closure of the union over all orderings of the subshifts arising from codings of the Pascal adic by the first edge has superpolynomial complexity, is not topologically transitive, and has no periodic points besides the two fixed points, while the intersection over all orderings consists of just four orbits.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 37 , Issue 7 , October 2017 , pp. 2131 - 2162
Copyright
© Cambridge University Press, 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adams, T. M. and Petersen, K. E.. Binomial-coefficient multiples of irrationals. Monatsh. Math. 125(4) (1998), 269–278.CrossRefGoogle Scholar
Bezuglyi, S., Kwiatkowski, J. and Medynets, K.. Aperiodic substitution systems and their Bratteli diagrams. Ergod. Th. & Dynam. Sys. 29(1) (2009), 37–72.CrossRefGoogle Scholar
Bezuglyi, S., Kwiatkowski, J., Medynets, K. and Solomyak, B.. Invariant measures on stationary Bratteli diagrams. Ergod. Th. & Dynam. Sys. 30(4) (2010), 973–1007.CrossRefGoogle Scholar
Bezuglyi, S., Kwiatkowski, J. and Yassawi, R.. Perfect orderings on finite rank Bratteli diagrams. Canad. J. Math. 66(1) (2014), 57–101.CrossRefGoogle Scholar
Bezuglyi, S. and Yassawi, R.. Perfect orderings on Bratteli diagrams II: general Bratteli diagrams. Preprint, 2014, arXiv:1306.1788 (in English).CrossRefGoogle Scholar
Downarowicz, T. and Maass, A.. Finite-rank Bratteli–Vershik diagrams are expansive. Ergod. Th. & Dynam. Sys. 28(3) (2008), 739–747.CrossRefGoogle Scholar
Durand, F.. Combinatorics on Bratteli diagrams and dynamical systems. Combinatorics, Automata and Number Theory (Encyclopedia of Mathematics and its Applications, 135) . Cambridge University Press, Cambridge, 2010, pp. 324–372.CrossRefGoogle Scholar
Durand, F., Host, B. and Skau, C.. Substitutional dynamical systems, Bratteli diagrams and dimension groups. Ergod. Th. & Dynam. Sys. 19(4) (1999), 953–993.CrossRefGoogle Scholar
Durand, F. and Yassawi, R.. Personal communication, 2014.Google Scholar
Forrest, A. H.. K-groups associated with substitution minimal systems. Israel J. Math. 98 (1997), 101–139.CrossRefGoogle Scholar
Frick, S. B.. Limited scope adic transformations. Discrete Contin. Dyn. Syst. Ser. S 2(2) (2009), 269–285.Google Scholar
Giordano, T., Putnam, I. F. and Skau, C. F.. Topological orbit equivalence and C ∗ -crossed products. J. Reine Angew. Math. 469 (1995), 51–111.Google Scholar
Gjerde, R. and Johansen, Ø.. Bratteli–Vershik models for Cantor minimal systems: applications to Toeplitz flows. Ergod. Th. & Dynam. Sys. 20(6) (2000), 1687–1710.CrossRefGoogle Scholar
Hahn, F. J.. Skew product transformations and the algebras generated by exp(p (n)). Illinois J. Math. 9 (1965), 178–190.CrossRefGoogle Scholar
Herman, R. H., Putnam, I. F. and Skau, C. F.. Ordered Bratteli diagrams, dimension groups and topological dynamics. Internat. J. Math. 3(6) (1992), 827–864.CrossRefGoogle Scholar
Host, B.. Substitution subshifts and Bratteli diagrams. Topics in Symbolic Dynamics and Applications (Temuco, 1997) (London Mathematical Society Lecture Note Series, 279) . Cambridge University Press, Cambridge, 2000, pp. 35–55.Google Scholar
Høynes, S.-M.. Finite-rank Bratteli–Vershik systems are expansive—a new proof. Preprint, 2014,arXiv:1411.3371 (in English).Google Scholar
Janssen, J., Quas, A. and Yassawi, R.. Bratteli diagrams where almost all orders are imperfect. Preprint, 2014, arXiv:1407.3496v2 (in English).Google Scholar
Keynes, H. B. and Robertson, J. B.. Eigenvalue theorems in topological transformation groups. Trans. Amer. Math. Soc. 139 (1969), 359–369.CrossRefGoogle Scholar
Livshitz, A.. A sufficient conditiuon for weak mixing of substitutions and stationary adic transformations. Math. Notes 44 (1988), 920–925 (in English and Russian).CrossRefGoogle Scholar
Medynets, K.. Cantor aperiodic systems and Bratteli diagrams. C. R. Math. Acad. Sci. Paris 342(1) (2006), 43–46 (in English, with English and French summaries).CrossRefGoogle Scholar
Méla, X. S.. Dynamical properties of the Pascal adic and related systems. ProQuest LLC, Ann Arbor, MI, 2002. PhD Thesis, The University of North Carolina at Chapel Hill.Google Scholar
Méla, X. and Petersen, K.. Dynamical properties of the Pascal adic transformation. Ergod. Th. & Dynam. Sys. 25(1) (2005), 227–256.CrossRefGoogle Scholar