Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-24T16:45:39.615Z Has data issue: false hasContentIssue false
  • English
  • Français

Dynamical degrees of Hurwitz correspondences

Part of: Projective and enumerative geometry Complex dynamical systems Curves Special varieties

Published online by Cambridge University Press:  04 December 2018

ROHINI RAMADAS
ROHINI RAMADAS*
Affiliation:
Department of Mathematics, Brown University, Providence, RI, USA email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 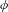$\unicode[STIX]{x1D719}$ be a post-critically finite branched covering of a two-sphere. By work of Koch, the Thurston pullback map induced by 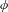$\unicode[STIX]{x1D719}$ on Teichmüller space descends to a multivalued self-map—a Hurwitz correspondence 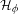${\mathcal{H}}_{\unicode[STIX]{x1D719}}$—of the moduli space 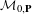${\mathcal{M}}_{0,\mathbf{P}}$. We study the dynamics of Hurwitz correspondences via numerical invariants called dynamical degrees. We show that the sequence of dynamical degrees of 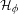${\mathcal{H}}_{\unicode[STIX]{x1D719}}$ is always non-increasing and that the behavior of this sequence is constrained by the behavior of 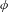$\unicode[STIX]{x1D719}$ at and near points of its post-critical set.

Keywords

dynamical degreescorrespondencesmoduli spaces

MSC classification

Primary: 14H10: Families, moduli (algebraic)
Secondary: 14N99: None of the above, but in this section 14M99: None of the above, but in this section 37F05: Relations and correspondences
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 40 , Issue 7 , July 2020 , pp. 1968 - 1990
Copyright
© Cambridge University Press, 2018

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arbarello, E. and Cornalba, M.. Calculating cohomology groups of moduli spaces of curves via algebraic geometry. Publ. Math. Inst. Hautes Études Sci. 88(1) (1998), 97–127.Google Scholar
Douady, A. and Hubbard, J. H.. A proof of Thurston’s topological characterization of rational functions. Acta Math. 171(2) (1993), 263–297.Google Scholar
Dinh, T.-C. and Sibony, N.. Une borne supérieure pour l’entropie topologique d’une application rationelle. Ann. of Math. (2) 161(3) (2005), 1637–1644.Google Scholar
Dinh, T.-C. and Sibony, N.. Upper bound for the topological entropy of a meromorphic correspondence. Israel J. Math. 163(1) (2008), 29–44.Google Scholar
Fulton, W.. Hurwitz schemes and irreducibility of moduli of algebraic curves. Ann. of Math. (2) 90(3) (1969), 542–575.Google Scholar
Fulton, W.. Intersection Theory, 2nd edn. Springer, New York, 1998.Google Scholar
Gromov, M.. On the entropy of holomorphic maps. Enseign. Math. 49 (2003), 217–235.Google Scholar
Guedj, V.. Ergodic properties of rational mappings with large topological degree. Ann. of Math. (2) 161(3) (2005), 1589–1607.Google Scholar
Hartshorne, R.. Algebraic Geometry (Encyclopaedia of Mathematical Sciences). Springer, New York, 1977.Google Scholar
Harris, J. and Mumford, D.. On the Kodaira dimension of the moduli space of curves. Invent. Math. 67 (1982), 23–86.Google Scholar
Ionel, E.-N.. Topological recursive relations in H 2g(𝓜g, n). Invent. Math. 148 (2002), 627–658.Google Scholar
Kapranov, M. M.. Veronese curves and Grothendieck–Knudsen moduli space 𝓜0, n. J. Algebraic Geom. 2(2) (1993), 239–262.Google Scholar
Koch, S.. Teichmüller theory and critically finite endomorphisms. Adv. Math. 248 (2013), 573–617.Google Scholar
Koch, S. and Roeder, R. K. W.. Computing dynamical degrees of rational maps on moduli space. Ergod. Th. & Dynam. Sys. 36(8) (2016), 2538–2579.Google Scholar
Lazarsfeld, R. K.. Positivity in Algebraic Geometry I. Springer, Berlin, Heidelberg, 2004.Google Scholar
Ramadas, R.. Dynamics on the moduli space of pointed rational curves. PhD Thesis, University of Michigan, 2017.Google Scholar
Ramadas, R.. Hurwitz correspondences on compactifications of 𝓜0, N. Adv. Math. 323 (2018), 622–667.Google Scholar
Romagny, M. and Wewers, S.. Hurwitz spaces. Sémin. Congr. 13 (2006), 313–341.Google Scholar
Silverman, J. H.. Integer points, Diophantine approximation, and iteration of rational maps. Duke Math. J. 71(3) (1993), 793–829.Google Scholar
Truong, T. T.. (Relative) dynamical degrees of rational maps over an algebraic closed field. Preprint, 2015, arXiv:1501.01523.Google Scholar
Truong, T. T.. Relative dynamical degrees of correspondences over a field of arbitrary characteristic. J. Reine Angew. Math. (2018), to appear.Google Scholar
Yomdin, Y.. Volume growth and entropy. Israel J. Math. 57(3) (1987), 285–300.Google Scholar