Published online by Cambridge University Press: 01 October 2021
We study the possible dynamical degrees of automorphisms of the affine space 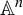 $\mathbb {A}^n$
. In dimension
$\mathbb {A}^n$
. In dimension 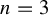 $n=3$
, we determine all dynamical degrees arising from the composition of an affine automorphism with a triangular one. This generalizes the easier case of shift-like automorphisms which can be studied in any dimension. We also prove that each weak Perron number is the dynamical degree of an affine-triangular automorphism of the affine space
$n=3$
, we determine all dynamical degrees arising from the composition of an affine automorphism with a triangular one. This generalizes the easier case of shift-like automorphisms which can be studied in any dimension. We also prove that each weak Perron number is the dynamical degree of an affine-triangular automorphism of the affine space 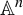 $\mathbb {A}^n$
for some n, and we give the best possible n for quadratic integers, which is either
$\mathbb {A}^n$
for some n, and we give the best possible n for quadratic integers, which is either 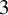 $3$
or
$3$
or 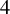 $4$
.
$4$
.