Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-28T03:56:53.265Z Has data issue: false hasContentIssue false
  • English
  • Français

Duality for automorphisms on a compact C*-dynamical system

Published online by Cambridge University Press:  19 September 2008

David E. Evans  and
Akitaka Kishimoto
David E. Evans
Affiliation:
University of Warwick, Coventry CVA 7AL, England
Akitaka Kishimoto
Affiliation:
University of Warwick, Coventry CVA 7AL, England
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

When considering an action α of a compact group G on a C*-algebra A, the notion of an α-invariant Hilbert space in A has proved extremely useful [1, 4, 8, 14, 17, 18]. Following Roberts [13] a Hilbert space in (a unital algebra) A is a closed subspace H of A such that x*y is a scalar for all x, y in H. For example if G is abelian, and α is ergodic in the sense that the fixed point algebra Aα is trivial, then A is generated as a Banach space by a unitary in each of the spectral subspaces

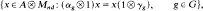
which are then invariant one dimensional Hilbert spaces. If G is not abelian, then Hilbert spaces (which are always assumed to be invariant) do not necessarily exist, even for ergodic actions. For non-ergodic actions, it is also desirable to relax the requirement to x*y being a constant multiple of some positive element of Aα. More generally, if γ is a finite dimensional matrix representation of G and n is a positive integer, we define 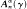to be the subspace

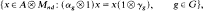
where d is the dimension d(γ) of γ, and Mnd denotes n×d complex matrices. (Usually we will denote the extended action of αg to αg ⊗ 1 on A⊗Mnd again by αg.) Let .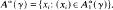

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 8 , Issue 2 , June 1988 , pp. 173 - 189
Copyright
Copyright © Cambridge University Press 1988

References

REFERENCES

[1]Araki, H., Haag, R., Kastler, D. & Takesaki, M.. Extensions of KMS states and chemical potential. Commun. Math. Phys. 53 (1977), 97–134.Google Scholar
[2]Bratteli, O., Elliott, G. A. & Robinson, D. W.. Strong topological transitivity and C*-dynamical systems. J. Math. Soc. Japan 37 (1985), 115–133.Google Scholar
[3]Bratteli, O. & Evans, D. E., Dynamical semigroups commuting with compact abelian actions. Ergod. Th. & Dynam. Sys. 3 (1983), 187–217.Google Scholar
[4]Bratteli, O. & Evans, D. E.. Derivations tangential to compact groups: The non-abelian case. Proc. Lon. Math. Soc. 52 No. 3 (1986), 369–384.CrossRefGoogle Scholar
[5]Bratteli, O., Elliott, G. A., Evans, D. E. & Kishimoto, A.. Quasi-product actions of a compact abelian group on a C*-algebra. Tôhoku Math. J. (to appear).Google Scholar
[6]Bratteli, O. & Jorgensen, P. E. T.. Derivations commuting with abelian gauge actions on lattice systems. Commun. Math. Phys. 87 (1982), 353–364.Google Scholar
[7]Bratteli, O. & Kishimoto, A.. Derivations and free group actions on C*-algebras. J. Operator Theory 15 (1986), 377–410.Google Scholar
[8]Bratteli, O., Kishimoto, A. & Robinson, D. W.. Embedding product type actions into C*-dynamical systems. J. Funct. Anal. 75 (1987), 188–210.CrossRefGoogle Scholar
[9]Glimm, J.. A Stone-Weierstrass theorem for C*-algebras. Ann. Math. 72 (1960), 216–244.CrossRefGoogle Scholar
[10]Longo, R., Peligrad, C.. Non-commutative topological dynamics and compact actions on C*-algebras. J. Funct. Anal. 58 (1984), 157–174.CrossRefGoogle Scholar
[11]Pedersen, G. K., C*-algebras and their Automorphism Groups. Academic Press: London, New York, San Francisco, 1979.Google Scholar
[12]Popa, S.. On a problem of R. V. Kadison on maximal abelian *-subalgebras in factors. Invent. Math. 65 (1981), 269–281.Google Scholar
[13]Powers, R. T. & Price, G. L.. Derivations vanishing on S(∞). Commun. Math. Phys. 84 (1982), 439–447.CrossRefGoogle Scholar
[14]Roberts, J. E.. Cross products of a von Neumann algebra by group duals. Symposia Math. 20 (1976), 335–363.Google Scholar
[15]Robinson, D. W., Stormer, E. & Takesaki, M.. Derivations of simple C*-algebras tangential to compact automorphism groups. J. Operator Theory 13 (1985), 189–200.Google Scholar
[16]Sakai, S.. C*-algebras and W*-algebras. Springer-Verlag: Berlin, Heidelberg, New York, 1971.Google Scholar
[17]Takesaki, M.. Fourier analysis of compact automorphism groups. (An application of Tannaka duality theorem), Algebres d'Operateurs et leurs Applications en Physique Mathematique (Editor, Kastler, D.), Editions du CNRS: Paris, 1979, pp. 361–372.Google Scholar
[18]Wassermann, A. J.. Automorphic actions of compact groups on operator algebras. Thesis, University of Pennsylvania (1981).Google Scholar