Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-28T10:45:50.402Z Has data issue: false hasContentIssue false
  • English
  • Français

The doubling map with asymmetrical holes

Published online by Cambridge University Press:  14 November 2013

PAUL GLENDINNING  and
NIKITA SIDOROV
PAUL GLENDINNING
Affiliation:
School of Mathematics, The University of Manchester, Oxford Road, Manchester M13 9PL, UK email [email protected]@manchester.ac.uk
NIKITA SIDOROV
Affiliation:
School of Mathematics, The University of Manchester, Oxford Road, Manchester M13 9PL, UK email [email protected]@manchester.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

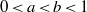Let $0\lt a\lt b\lt 1$ and let 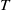$T$ be the doubling map. Set 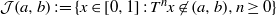$ \mathcal{J} (a, b): = \{ x\in [0, 1] : {T}^{n} x\not\in (a, b), n\geq 0\} $. In this paper we completely characterize the holes 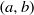$(a, b)$ for which any of the following scenarios hold: (i) 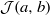$ \mathcal{J} (a, b)$ contains a point 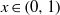$x\in (0, 1)$; (ii) 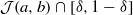$ \mathcal{J} (a, b)\cap [\delta , 1- \delta ] $ is infinite for any fixed 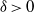$\delta \gt 0$; (iii) 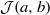$ \mathcal{J} (a, b)$ is uncountable of zero Hausdorff dimension; (iv) 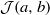$ \mathcal{J} (a, b)$ is of positive Hausdorff dimension. In particular, we show that (iv) is always the case if

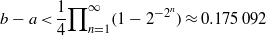$$\begin{eqnarray*}b- a\lt \frac{1}{4} { \mathop{\prod }\nolimits}_{n= 1}^{\infty } (1- {2}^{- {2}^{n} } )\approx 0. 175\hspace{0.167em} 092\end{eqnarray*}$$
and that this bound is sharp. As a corollary, we give a full description of first- and second-order critical holes introduced by N. Sidorov [Supercritical holes for the doubling map. Preprint, see http://arxiv.org/abs/1204.1920] for the doubling map. Furthermore, we show that our model yields a continuum of ‘routes to chaos’ via arbitrary sequences of products of natural numbers, thus generalizing the standard route to chaos via period doubling.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 35 , Issue 4 , June 2015 , pp. 1208 - 1228
Copyright
© Cambridge University Press, 2013 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Allouche, J.-P., Clarke, M. and Sidorov, N.. Periodic unique beta-expansions: the Sharkovskiĭ ordering. Ergod. Th. & Dynam. Sys. 29 (2009), 1055–1074.CrossRefGoogle Scholar
Allouche, J.-P. and Glen, A.. Distribution modulo 1 and the lexicographic world. Ann. Sci. Math. Québec 33 (2009), 125–143.Google Scholar
Bullett, S. and Sentenac, P.. Ordered orbits of the shift, square roots, and the devil’s staircase. Math. Proc. Cambridge Philos. Soc. 115 (1994), 451–481.CrossRefGoogle Scholar
Bundfuss, S., Krüger, T. and Troubetzkoy, S.. Topological and symbolic dynamics for hyperbolic systems with holes. Ergod. Th. & Dynam. Sys. 31 (2011), 1305–1323.CrossRefGoogle Scholar
Chernov, N. and Markarian, R.. Ergodic properties of Anosov maps with rectangular holes. Bol. Soc. Bras. Mat. 28 (1997), 271–314.CrossRefGoogle Scholar
Chernov, N. and Markarian, R.. Anosov maps with rectangular holes. Bol. Soc. Bras. Mat. 28 (1997), 315–342.CrossRefGoogle Scholar
Chernov, N., Markarian, R. and Troubetzkoy, S.. Invariant measures for Anosov maps with small holes. Ergod. Th. & Dynam. Sys. 20 (2000), 1007–1044.CrossRefGoogle Scholar
Collet, J. -P. and Eckmann, J. P.. Iterated Maps on the Interval as Dynamical Systems. Birkhäuser, Basel, 1980.Google Scholar
Gambaudo, J. M., Lanford III, O. and Tresser, C.. Dynamique symbolique des rotations. C. R. Acad. Sci. Paris (Série I) 299 (1984), 823–826.Google Scholar
Gambaudo, J. M., Procaccia, I., Thomae, S. and Tresser, C.. New universal scenarios for the onset of chaos in Lorenz-type flows. Phys. Rev. Lett. 57 (1985), 925–928.CrossRefGoogle Scholar
Glendinning, P.. Chaos and Routes to Chaos in Lorenz Maps. Adams Prize Essay, University of Cambridge, 1992.Google Scholar
Glendinning, P. and Hall, T.. Zeros of the kneading invariant and topological entropy for Lorenz maps. Nonlinearity 9 (1996), 999–1014.CrossRefGoogle Scholar
Glendinning, P. and Sidorov, N.. Unique representations of real numbers in non-integer bases. Math. Res. Lett. 8 (2001), 535–543.CrossRefGoogle Scholar
Glendinning, P. and Sparrow, C.. Prime and renormalisable kneading invariants and the dynamics of expanding Lorenz maps. Phys. D 62 (1993), 22–50.CrossRefGoogle Scholar
Goldberg, L. and Tresser, C.. Rotation orbits and the Farey tree. Ergod. Th. & Dynam. Sys. 16 (1996), 1011–1029.CrossRefGoogle Scholar
Hardy, G. H. and Wright, E. M.. An Introduction to the Theory of Numbers, 5th edn. Clarendon Press, Oxford, 1979.Google Scholar
Hubbard, J. H. and Sparrow, C. T.. The classification of topologically expansive Lorenz maps. Comm. Pure Appl. Math. 43 (1990), 431–443.CrossRefGoogle Scholar
Labarca, R. and Moreira, C. G.. Essential dynamics for Lorenz maps on the real line and the lexicographic world. Ann. Inst. H. Poincaré 23 (2006), 683–694.Google Scholar
Lothaire, M.. Algebraic Combinatorics On Words (Encyclopedia of Mathematics and its Applications). Cambridge University Press, Cambridge, 2002.CrossRefGoogle Scholar
MacKay, R. S. and Tresser, C.. Transition to topological chaos for circle maps. Phys. D 19 (1986), 206–237.CrossRefGoogle Scholar
Mauldin, D. and Urbański, M.. Dimensions and measures in infinite iterated function systems. Proc. Lond. Math. Soc. 73 (1996), 105–154.CrossRefGoogle Scholar
Mignosi, F.. On the number of factors of Sturmian words. Theoret. Comput. Sci. 82 (1991), 71–84.CrossRefGoogle Scholar
Milnor, W. and Thurston, W.. On iterated maps of the interval. Dynamical Systems (College Park, MD, 1986–87 (Lecture Notes in Mathematics, 1342). Springer, Berlin, 1988, pp. 465–563.Google Scholar
Sidorov, N.. Arithmetic dynamics. Topics in Dynamics and Ergodic Theory (London Mathematical Society Lecture Note Series, 310). Cambridge University Press, Cambridge, 2003, pp. 145–189.CrossRefGoogle Scholar
Sidorov, N.. Supercritical holes for the doubling map. Preprint, see http://arxiv.org/abs/1204.1920.Google Scholar
Thue–Morse constant, http://mathworld.wolfram.com/Thue-MorseConstant.html.Google Scholar