Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-23T17:58:14.388Z Has data issue: false hasContentIssue false
  • English
  • Français

Divergence, undistortion and Hölder continuous cocycle superrigidity for full shifts

Part of: Topological dynamics Special aspects of infinite or finite groups Ergodic theory

Published online by Cambridge University Press:  02 June 2020

NHAN-PHU CHUNG  and
YONGLE JIANG Open the ORCID record for YONGLE JIANG [Opens in a new window]
NHAN-PHU CHUNG
Affiliation:
Department of Mathematics, Sungkyunkwan University, Suwon440-746, Korea (e-mail: [email protected], [email protected])
YONGLE JIANG
Affiliation:
School of Mathematical Sciences, Dalian University of Technology, Dalian, 116024, China (e-mail: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

In this article, we will prove a full topological version of Popa’s measurable cocycle superrigidity theorem for full shifts [Popa, Cocycle and orbit equivalence superrigidity for malleable actions of $w$-rigid groups. Invent. Math. 170(2) (2007), 243–295]. Let 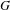$G$ be a finitely generated group that has one end, undistorted elements and sub-exponential divergence function. Let 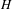$H$ be a target group that is complete and admits a compatible bi-invariant metric. Then, every Hölder continuous cocycle for the full shifts of 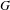$G$ with value in 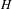$H$ is cohomologous to a group homomorphism via a Hölder continuous transfer map. Using the ideas of Behrstock, Druţu, Mosher, Mozes and Sapir [Divergence, thick groups, and short conjugators. Illinois J. Math. 58(4) (2014), 939–980; Thick metric spaces, relative hyperbolicity, and quasi-isometric rigidity. Math. Ann. 344(3) (2009), 543–595; Divergence in lattices in semisimple Lie groups and graphs of groups. Trans. Amer. Math. Soc. 362(5) (2010), 2451–2505; Tree-graded spaces and asymptotic cones of groups. Topology 44(5) (2005), 959–1058], we show that the class of our acting groups is large including wide groups having undistorted elements and one-ended groups with strong thick of finite orders. As a consequence, irreducible uniform lattices of most of higher rank connected semisimple Lie groups, mapping class groups of $g$-genus surfaces with 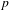$p$-punches, 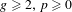$g\geq 2,p\geq 0$; Richard Thompson groups 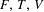$F,T,V$; 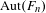$\text{Aut}(F_{n})$, 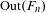$\text{Out}(F_{n})$, 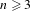$n\geq 3$; certain (two-dimensional) Coxeter groups; and one-ended right-angled Artin groups are in our class. This partially extends the main result in Chung and Jiang [Continuous cocycle superrigidity for shifts and groups with one end. Math. Ann. 368(3–4) (2017), 1109–1132].

Keywords

Hölder continuous cocycle superrigiditydivergence functionsundistortionone-ended groupsfull shifts

MSC classification

Primary: 37A20: Orbit equivalence, cocycles, ergodic equivalence relations 37B05: Transformations and group actions with special properties (minimality, distality, proximality, etc.)
Secondary: 37B10: Symbolic dynamics 20F65: Geometric group theory
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 41 , Issue 8 , August 2021 , pp. 2274 - 2293
Check for updates
Copyright
© The Author(s) 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alibegović, E.. Translation lengths in Out(F n). Geom. Dedicata 92 (2002), 87–93.Google Scholar
Alonso, J. M., Brady, T., Cooper, D., Ferlini, V., Lustig, M., Mihalik, M., Shapiro, M. and Short, H.. Notes on word hyperbolic groups. Group Theory from a Geometrical Viewpoint (Trieste, 1990). Ed. Short, H.. World Scientific, River Edge, NJ, 1991, pp. 3–63.Google Scholar
Behrstock, J. and Charney, R.. Divergence and quasimorphisms of right-angled Artin groups. Math. Ann. 352(2) (2012), 339–356.Google Scholar
Behrstock, J. and Druţu, C.. Divergence, thick groups, and short conjugators. Illinois J. Math. 58(4) (2014), 939–980.Google Scholar
Behrstock, J., Druţu, C. and Mosher, L.. Thick metric spaces, relative hyperbolicity, and quasi-isometric rigidity. Math. Ann. 344(3) (2009), 543–595.Google Scholar
Bleak, C., Bowman, H., Lynch, A. Gordon, Graham, G., Hughes, J., Matucci, F. and Sapir, E.. Centralizers in the R. Thompson group V n . Groups Geom. Dyn. 7(4) (2013), 821–865.Google Scholar
Brady, N. and Meier, J.. Connectivity at infinity for right angled Artin groups. Trans. Amer. Math. Soc. 353(1) (2001), 117–132.Google Scholar
Bridson, M. R. and Haefliger, A.. Metric Spaces of Non-Positive Curvature (Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], 319). Springer, Berlin, 1999.Google Scholar
Burillo, J.. Quasi-isometrically embedded subgroups of Thompson’s group F . J. Algebra 212(1) (1999), 65–78.Google Scholar
Burillo, J., Cleary, S., Stein, M. and Taback, J.. Combinatorial and metric properties of Thompson’s group T . Trans. Amer. Math. Soc. 361(2) (2009), 631–652.Google Scholar
Calegari, D. and Freedman, M. H.. Distortion in transformation groups. Geom. Topol. 10 (2006), 267–293 With an appendix by Yves de Cornulier.Google Scholar
Chung, N. and Jiang, Y.. Continuous cocycle superrigidity for shifts and groups with one end. Math. Ann. 368(3–4) (2017), 1109–1132.Google Scholar
Cohen, D. B.. Continuous cocycle superrigidity for the full shift over a finitely generated torsion group. Int. Math. Res. Not. IMRN 6 (2020), 1610–1620.Google Scholar
Culler, M. and Vogtmann, K.. A group-theoretic criterion for property FA. Proc. Amer. Math. Soc. 124(3) (1996), 677–683.Google Scholar
Dani, P. and Thomas, A.. Divergence in right-angled Coxeter groups. Trans. Amer. Math. Soc. 367(5) (2015), 3549–3577.Google Scholar
Davis, M. W.. The Geometry and Topology of Coxeter Groups (London Mathematical Society Monographs Series, 32). Princeton University Press, Princeton, NJ, 2008.Google Scholar
Druţu, C., Mozes, S. and Sapir, M.. Divergence in lattices in semisimple Lie groups and graphs of groups. Trans. Amer. Math. Soc. 362(5) (2010), 2451–2505.Google Scholar
Druţu, C. and Sapir, M.. Tree-graded spaces and asymptotic cones of groups. Topology 44(5) (2005), 959–1058. With an appendix by Denis Osin and Mark Sapir.Google Scholar
Epstein, D. B. A., Cannon, J. W., Holt, D. F., Levy, S. V. F., Paterson, M. S. and Thurston, W. P.. Word Processing in Groups. Jones and Bartlett Publishers, Boston, MA, 1992.Google Scholar
Farb, B.. Combing lattices in semisimple Lie groups. Groups—Korea ’94 (Pusan). de Gruyter, Berlin, 1995, pp. 57–67.Google Scholar
Farb, B., Lubotzky, A. and Minsky, Y.. Rank-1 phenomena for mapping class groups. Duke Math. J. 106(3) (2001), 581–597.Google Scholar
Franks, J. and Handel, M.. Distortion elements in group actions on surfaces. Duke Math. J. 131(3) (2006), 441–468.Google Scholar
Furman, A.. On Popa’s cocycle superrigidity theorem. Int. Math. Res. Not. IMRN 19 (2007), Art. ID rnm073, 46.Google Scholar
Gersten, S. M.. Quadratic divergence of geodesics in CAT(0) spaces. Geom. Funct. Anal. 4(1) (1994), 37–51.Google Scholar
Gersten, S. M. and Short, H. B.. Rational subgroups of biautomatic groups. Ann. of Math. (2) 134(1) (1991), 125–158.Google Scholar
Golan, G. and Sapir, M.. Divergence functions of Thompson groups. Geom. Dedicata 201 (2019), 227–242.Google Scholar
Gromov, M.. Hyperbolic groups. Essays in Group Theory (Mathematical Science Research Institute Publications, 8). Springer, New York, 1987, pp. 75–263.Google Scholar
Gromov, M.. Asymptotic invariants of infinite groups. Geometric Group Theory, Vol. 2 (Sussex, 1991) (London Mathematical Society Lecture Note Series, 182). Cambridge University Press, Cambridge, 1993, pp. 1–295.Google Scholar
Katok, A. and Niţică, V.. Rigidity in Higher Rank Abelian Group Actions. Volume I (Cambridge Tracts in Mathematics, 185). Cambridge University Press, Cambridge, 2011.Google Scholar
Katok, A. B. and Schmidt, K.. The cohomology of expansive Z d -actions by automorphisms of compact, abelian groups. Pacific J. Math. 170(1) (1995), 105–142.Google Scholar
Katok, A. and Spatzier, R. J.. First cohomology of Anosov actions of higher rank abelian groups and applications to rigidity. Publ. Math. Inst. Hautes Études Sci. 79 (1994), 131–156.Google Scholar
Kleiner, B. and Leeb, B.. Rigidity of quasi-isometries for symmetric spaces and Euclidean buildings. Publ. Math. Inst. Hautes Études Sci. 86 (1997), 115–197.Google Scholar
Li, X.. Continuous orbit equivalence rigidity. Ergod. Th. & Dynam. Sys. 38(4) (2018), 1543–1563.Google Scholar
Meier, J.. Geometric invariants for Artin groups. Proc. Lond. Math. Soc. (3) 74(1) (1997), 151–173.Google Scholar
Ol’shanskii, A. Y., Osin, D. V. and Sapir, M. V.. Lacunary hyperbolic groups. Geom. Topol. 13(4) (2009), 2051–2140. With an appendix by Michael Kapovich and Bruce Kleiner.Google Scholar
Popa, S.. Cocycle and orbit equivalence superrigidity for malleable actions of w-rigid groups. Invent. Math. 170(2) (2007), 243–295.Google Scholar
Popa, S.. On the superrigidity of malleable actions with spectral gap. J. Amer. Math. Soc. 21(4) (2008), 981–1000.Google Scholar
Polterovich, L.. Growth of maps, distortion in groups and symplectic geometry. Invent. Math. 150(3) (2002), 655–686.Google Scholar
Schmidt, K.. The cohomology of higher-dimensional shifts of finite type. Pacific J. Math. 170(1) (1995), 237–269.Google Scholar
Serre, J.-P.. Trees. Springer, Berlin–New York, 1980, translated from the French by Stillwell, John.Google Scholar
Walters, P.. An Introduction to Ergodic Theory (Graduate Texts in Mathematics, 79). Springer, New York, 1982.Google Scholar