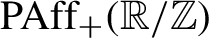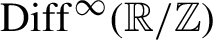1 Introduction
Let G be a group with some finite generating set
![]() $\mathcal G$
. We define the metric
$\mathcal G$
. We define the metric
![]() $d_{\mathcal G}$
on G by taking
$d_{\mathcal G}$
on G by taking
![]() $d_{\mathcal G} (g_{1}, g_{2})$
to be the infimum over all
$d_{\mathcal G} (g_{1}, g_{2})$
to be the infimum over all
![]() $k\ge 0$
such that there exist
$k\ge 0$
such that there exist
![]() $f_{1},\ldots , f_{k}\in \mathcal G$
and
$f_{1},\ldots , f_{k}\in \mathcal G$
and
![]() $\epsilon _{1},\ldots ,\epsilon _{k}\in \{-1, 1\}$
satisfying
$\epsilon _{1},\ldots ,\epsilon _{k}\in \{-1, 1\}$
satisfying
 $g_{2}=f_{1}^{\epsilon _{1}}\cdots f_{k}^{\epsilon _{k}}g_{1}$
.
$g_{2}=f_{1}^{\epsilon _{1}}\cdots f_{k}^{\epsilon _{k}}g_{1}$
.
Now let H be an arbitrary group. An element
![]() $f\in H$
is called distorted in H if there exists a finitely generated subgroup
$f\in H$
is called distorted in H if there exists a finitely generated subgroup
![]() $G\subset H$
containing f such that
$G\subset H$
containing f such that
 $$ \begin{align*} \lim_{n\to\infty}\frac{d_{\mathcal G}(f^{n}, \text{id})}{n}=0 \end{align*} $$
$$ \begin{align*} \lim_{n\to\infty}\frac{d_{\mathcal G}(f^{n}, \text{id})}{n}=0 \end{align*} $$
for some (and hence every) generating set
![]() $\mathcal G$
. Since the limit always exists, it is enough to verify it for some subsequence. The notion of distortion comes from geometric group theory and was introduced by Gromov in [Reference Gromov7].
$\mathcal G$
. Since the limit always exists, it is enough to verify it for some subsequence. The notion of distortion comes from geometric group theory and was introduced by Gromov in [Reference Gromov7].
The problem of the existence of distorted elements in some groups of homeomorphisms has been intensively studied for many years (see [Reference Calegari and Freedman2, Reference Dinamarca and Escayola3–Reference Franks and Handel6, Reference Guelmann and Liousse8, Reference Navas10, Reference Polterovich11]). Substantial progress has been achieved for groups of diffeomorphisms of manifolds. In particular, Avila [Reference Avila1] proved that rotations with irrational rotation number are distorted in the group of smooth diffeomorphisms of the circle. In this note we give a constructive proof that all irrational rotations are distorted both in the group of piecewise affine circle homeomorphisms,
![]() $\text {PAff}_{+}({\mathbb R/\mathbb Z})$
, and in the group of smooth circle diffeomorphisms,
$\text {PAff}_{+}({\mathbb R/\mathbb Z})$
, and in the group of smooth circle diffeomorphisms,
![]() ${\operatorname {\mathrm {Diff}}}^{{\kern1pt}\infty }(\mathbb R/\mathbb Z)$
. The result gives an answer to Question 11 in [Reference Navas9] (see also Question 2.5 in [Reference Franks, Crovisier, Franks, Gambaudo and Le Calvez5]). So far it has not even been known whether there exist distorted elements in
${\operatorname {\mathrm {Diff}}}^{{\kern1pt}\infty }(\mathbb R/\mathbb Z)$
. The result gives an answer to Question 11 in [Reference Navas9] (see also Question 2.5 in [Reference Franks, Crovisier, Franks, Gambaudo and Le Calvez5]). So far it has not even been known whether there exist distorted elements in
![]() $\text {PAff}_{+}(\mathbb R/\mathbb Z)$
. Now from [Reference Guelmann and Liousse8] it follows that each distorted element is conjugate to a rotation.
$\text {PAff}_{+}(\mathbb R/\mathbb Z)$
. Now from [Reference Guelmann and Liousse8] it follows that each distorted element is conjugate to a rotation.
From now on let G be either
![]() $\text {PAff}_{+}(\mathbb R/\mathbb Z)$
or
$\text {PAff}_{+}(\mathbb R/\mathbb Z)$
or
![]() ${\operatorname {\mathrm {Diff}}}^{{\kern1pt}\infty }(\mathbb R/\mathbb Z)$
. We say that
${\operatorname {\mathrm {Diff}}}^{{\kern1pt}\infty }(\mathbb R/\mathbb Z)$
. We say that
![]() $g\in G$
is trivial on some set if there exists a non-empty open set
$g\in G$
is trivial on some set if there exists a non-empty open set
![]() $I\subset [0,1)$
such that
$I\subset [0,1)$
such that
![]() $g(x)=x$
for
$g(x)=x$
for
![]() $x\in I$
. The set of all homeomorphisms in G which are trivial on some set will be denoted by
$x\in I$
. The set of all homeomorphisms in G which are trivial on some set will be denoted by
![]() $G_{\text {triv}}$
. By
$G_{\text {triv}}$
. By
![]() $\text {T}$
we denote the set of all rotations, and let
$\text {T}$
we denote the set of all rotations, and let
![]() $T_{\alpha }$
be the rotation with rotation number
$T_{\alpha }$
be the rotation with rotation number
![]() $\alpha $
.
$\alpha $
.
This paper is devoted to the proof of the following theorem.
Theorem. All irrational rotations are distorted in G.
2 Proofs
We first formulate two lemmas and deduce the theorem. The proofs of the lemmas will be given at the end of the paper.
Lemma 1. For any irrational rotation
![]() $T_{\alpha }$
and
$T_{\alpha }$
and
![]() $g\in G_{\text {triv}}\cup \text {T}$
there exist a finite generating set
$g\in G_{\text {triv}}\cup \text {T}$
there exist a finite generating set
![]() $\mathcal G_{g}\subset G$
and a constant
$\mathcal G_{g}\subset G$
and a constant
![]() $C>0$
such that
$C>0$
such that
Lemma 2. In G there exist
![]() $g_{1},\ldots , g_{l}\in G_{\text {triv}}\cup \text {T}$
and
$g_{1},\ldots , g_{l}\in G_{\text {triv}}\cup \text {T}$
and
![]() $k, k_{1},\ldots , k_{l}\in {\mathbb Z}$
with
$k, k_{1},\ldots , k_{l}\in {\mathbb Z}$
with
![]() $k\neq k_{1}+\cdots +k_{l}$
, such that for each sufficiently small
$k\neq k_{1}+\cdots +k_{l}$
, such that for each sufficiently small
![]() $\beta>0$
the element
$\beta>0$
the element
![]() $x=T_{\beta }$
satisfies
$x=T_{\beta }$
satisfies
Proof of the theorem
Fix an irrational rotation
![]() $T_{\alpha }$
. From Lemma 2 it follows that in G there exists an equation of the form (1) such that
$T_{\alpha }$
. From Lemma 2 it follows that in G there exists an equation of the form (1) such that
![]() $x=T_{\beta }$
, for all sufficiently small
$x=T_{\beta }$
, for all sufficiently small
![]() $\beta $
, is its solution. Let
$\beta $
, is its solution. Let
![]() $\mathcal G=\mathcal G_{g_{1}}\cup \cdots \cup \mathcal G_{g_{l}}$
, where
$\mathcal G=\mathcal G_{g_{1}}\cup \cdots \cup \mathcal G_{g_{l}}$
, where
![]() $\mathcal G_{g_{i}}$
,
$\mathcal G_{g_{i}}$
,
![]() $i=1,\ldots , l$
, are finite generating sets derived from Lemma 1 for
$i=1,\ldots , l$
, are finite generating sets derived from Lemma 1 for
![]() $T_{\alpha }$
. We may rewrite equation (1) in the form
$T_{\alpha }$
. We may rewrite equation (1) in the form
Let
![]() $\beta _{0}$
be a positive constant such that
$\beta _{0}$
be a positive constant such that
![]() $x=T_{\beta }$
for
$x=T_{\beta }$
for
![]() $\beta \in (0, \beta _{0})$
satisfies (2). Set
$\beta \in (0, \beta _{0})$
satisfies (2). Set
![]() $m:=k-k_{1}-\cdots -k_{l}$
, and let
$m:=k-k_{1}-\cdots -k_{l}$
, and let
![]() $(n_{i})$
be an increasing sequence of integers such that
$(n_{i})$
be an increasing sequence of integers such that
![]() $n_{i}\alpha \in (0, \beta _{0})\, (\text {mod}\, 1)$
. From Lemma 1 it follows that
$n_{i}\alpha \in (0, \beta _{0})\, (\text {mod}\, 1)$
. From Lemma 1 it follows that
 $$ \begin{align*} d_{\mathcal G}(T_{\alpha}^{n_{i}(k_{1}+\cdots+k_{j})} g_{j} T_{\alpha}^{-n_{i}(k_{1}+\cdots+k_{j})}, \text{id})\le C_{j}\log n_{i}\quad\text{for all }i\ge 1\text{ and }j=1,\ldots, l. \end{align*} $$
$$ \begin{align*} d_{\mathcal G}(T_{\alpha}^{n_{i}(k_{1}+\cdots+k_{j})} g_{j} T_{\alpha}^{-n_{i}(k_{1}+\cdots+k_{j})}, \text{id})\le C_{j}\log n_{i}\quad\text{for all }i\ge 1\text{ and }j=1,\ldots, l. \end{align*} $$
Since
![]() $x=T_{n_{i}\alpha }$
satisfies (2), we obtain
$x=T_{n_{i}\alpha }$
satisfies (2), we obtain
 $$ \begin{align*} d_{\mathcal G}(T_{\alpha}^{n_{i} m}, \text{id})\le \sum_{j=1}^{l} C_{j}\log n_{i}:= C \log n_{i}\quad\text{for all }i\ge 1\text{.} \end{align*} $$
$$ \begin{align*} d_{\mathcal G}(T_{\alpha}^{n_{i} m}, \text{id})\le \sum_{j=1}^{l} C_{j}\log n_{i}:= C \log n_{i}\quad\text{for all }i\ge 1\text{.} \end{align*} $$
Hence
 $$ \begin{align*} \lim_{n\to\infty}\frac{d_{\mathcal G}(T_{\alpha}^{n}, \text{id})}{n}= \lim_{i\to\infty}\frac{d_{\mathcal G}(T_{\alpha}^{n_{i} m}, \text{id})}{n_{i} m}\le \frac{C}{m}\lim_{i\to\infty} \frac{\log n_{i}}{n_{i}}=0 \end{align*} $$
$$ \begin{align*} \lim_{n\to\infty}\frac{d_{\mathcal G}(T_{\alpha}^{n}, \text{id})}{n}= \lim_{i\to\infty}\frac{d_{\mathcal G}(T_{\alpha}^{n_{i} m}, \text{id})}{n_{i} m}\le \frac{C}{m}\lim_{i\to\infty} \frac{\log n_{i}}{n_{i}}=0 \end{align*} $$
and the proof is complete.
Proof of Lemma 1
The proof relies on the observation that for a given interval
![]() $I\subset (0, 1)$
there exists a finite generating set
$I\subset (0, 1)$
there exists a finite generating set
![]() $\mathcal G\subset G$
such that for any
$\mathcal G\subset G$
such that for any
![]() $n\ge 1$
there exists a homeomorphism
$n\ge 1$
there exists a homeomorphism
![]() $h_{n}$
with
$h_{n}$
with
![]() $d_{\mathcal G}(h_{n}, \text {id})\le C\log n$
for some constant
$d_{\mathcal G}(h_{n}, \text {id})\le C\log n$
for some constant
![]() $C>0$
independent of n, and
$C>0$
independent of n, and
![]() $h_{n}(x)=T_{\alpha }^{n}(x)$
for
$h_{n}(x)=T_{\alpha }^{n}(x)$
for
![]() $x\notin I$
. Without loss of generality we may assume that
$x\notin I$
. Without loss of generality we may assume that
![]() $I=(a, 1).$
Let
$I=(a, 1).$
Let
![]() $m\ge 1$
be an integer such that
$m\ge 1$
be an integer such that
![]() $a+2/m<1$
. Let
$a+2/m<1$
. Let
![]() $h\in G $
be any homeomorphism such that
$h\in G $
be any homeomorphism such that
![]() $h(x)=x/2$
for
$h(x)=x/2$
for
![]() $x\in [0, a+2/m)$
, and let
$x\in [0, a+2/m)$
, and let
![]() $r(x)=x+1/m$
.
$r(x)=x+1/m$
.
We shall define
![]() $h_{n}$
by induction. Set
$h_{n}$
by induction. Set
![]() $h_{0}=\text {id}$
. If n is odd we put
$h_{0}=\text {id}$
. If n is odd we put
![]() $h_{n}=T_{\alpha } h_{n-1}$
. If n is even, we take
$h_{n}=T_{\alpha } h_{n-1}$
. If n is even, we take
![]() $s_{n}:=h_{n/2} h$
and observe that
$s_{n}:=h_{n/2} h$
and observe that
![]() $s_{n}((0, a))=(n\alpha /2, a/2+n\alpha /2)$
. Let
$s_{n}((0, a))=(n\alpha /2, a/2+n\alpha /2)$
. Let
![]() $k\in \{1,\ldots , m\}$
be such that
$k\in \{1,\ldots , m\}$
be such that
![]() $n\alpha /2+k/m\in [0, 1/m)$
(mod
$n\alpha /2+k/m\in [0, 1/m)$
(mod
![]() $1$
). Then
$1$
). Then
![]() $r^{k} s_{n}((0, a))\subset (0, a/2+1/m)$
. Therefore
$r^{k} s_{n}((0, a))\subset (0, a/2+1/m)$
. Therefore
 $$ \begin{align} h^{-1} r^{k} h_{n/2} h(x)=2(x/2+n\alpha/2+k/m)=x+n\alpha+2k/m=T_{\alpha}^{n}(x)+2k/m \end{align} $$
$$ \begin{align} h^{-1} r^{k} h_{n/2} h(x)=2(x/2+n\alpha/2+k/m)=x+n\alpha+2k/m=T_{\alpha}^{n}(x)+2k/m \end{align} $$
for
![]() $x\in (0, a)$
. Put
$x\in (0, a)$
. Put
 $h_{n}:=r^{-2k}h^{-1} r^{k} h_{n/2} h$
, and let
$h_{n}:=r^{-2k}h^{-1} r^{k} h_{n/2} h$
, and let
![]() $\mathcal G:=\{T_{\alpha }, h, r\}$
. Note that
$\mathcal G:=\{T_{\alpha }, h, r\}$
. Note that
Thus we obtain
![]() $d_{\mathcal G}(h_{n}, \text {id})\le C\log n$
. Finally, observe that for any
$d_{\mathcal G}(h_{n}, \text {id})\le C\log n$
. Finally, observe that for any
![]() $g\in G_{\text {triv}}$
such that
$g\in G_{\text {triv}}$
such that
![]() $g(x)=\text {id}$
on I we have
$g(x)=\text {id}$
on I we have
 $$ \begin{align} T_{\alpha}^{n} g T_{\alpha}^{-n}=h_{n} g h_{n}^{-1}. \end{align} $$
$$ \begin{align} T_{\alpha}^{n} g T_{\alpha}^{-n}=h_{n} g h_{n}^{-1}. \end{align} $$
Indeed, from (3) and the definition of
![]() $h_{n}$
and r it follows that
$h_{n}$
and r it follows that
![]() $h_{n}(x)=T_{\alpha }^{n}(x)$
for
$h_{n}(x)=T_{\alpha }^{n}(x)$
for
![]() $x\in (0, a)$
, and
$x\in (0, a)$
, and
Therefore, we have
 $$ \begin{align*} h_{n}^{-1}(x)=T_{\alpha}^{-n}(x)\in (0, a)\quad\text{for }x\in (n\alpha, a+n\alpha). \end{align*} $$
$$ \begin{align*} h_{n}^{-1}(x)=T_{\alpha}^{-n}(x)\in (0, a)\quad\text{for }x\in (n\alpha, a+n\alpha). \end{align*} $$
Since
![]() $g(x)=x$
for
$g(x)=x$
for
![]() $x\in (a, 1)$
and g is a homeomorphism, we have
$x\in (a, 1)$
and g is a homeomorphism, we have
![]() $g((0, a))=(0, a)$
.
$g((0, a))=(0, a)$
.
To justify equality (4), first fix
![]() $x\in (n\alpha , a+n\alpha )$
. Then we have
$x\in (n\alpha , a+n\alpha )$
. Then we have
 $$ \begin{align*} h_{n}^{-1}(x)=T_{\alpha}^{-n}(x)\in (0, a) \end{align*} $$
$$ \begin{align*} h_{n}^{-1}(x)=T_{\alpha}^{-n}(x)\in (0, a) \end{align*} $$
and
 $$ \begin{align*} (gh_{n}^{-1})(x)=(gT_{\alpha}^{-n})(x)\in (0, a). \end{align*} $$
$$ \begin{align*} (gh_{n}^{-1})(x)=(gT_{\alpha}^{-n})(x)\in (0, a). \end{align*} $$
Consequently, we obtain
 $$ \begin{align*} h_{n}gh_{n}^{-1}(x)=T_{\alpha}^{n}gT_{\alpha}^{-n}(x)\quad\text{for }x\in (n\alpha, a+n\alpha), \end{align*} $$
$$ \begin{align*} h_{n}gh_{n}^{-1}(x)=T_{\alpha}^{n}gT_{\alpha}^{-n}(x)\quad\text{for }x\in (n\alpha, a+n\alpha), \end{align*} $$
by the fact that
![]() $h_{n}(x)=T_{\alpha }^{n}(x)$
for
$h_{n}(x)=T_{\alpha }^{n}(x)$
for
![]() $x\in (0, a)$
. On the other hand, if
$x\in (0, a)$
. On the other hand, if
![]() $x\notin (n\alpha , a+n\alpha )$
, from (5) and the fact that
$x\notin (n\alpha , a+n\alpha )$
, from (5) and the fact that
![]() $T_{\alpha }^{n}$
and
$T_{\alpha }^{n}$
and
![]() $h_{n}$
are homeomorphisms, we obtain
$h_{n}$
are homeomorphisms, we obtain
 $$ \begin{align*} T_{\alpha}^{-n}(x)\in (a, 1]\quad\text{and}\quad h_{n}^{-1}(x)\in(a, 1]. \end{align*} $$
$$ \begin{align*} T_{\alpha}^{-n}(x)\in (a, 1]\quad\text{and}\quad h_{n}^{-1}(x)\in(a, 1]. \end{align*} $$
Since
![]() $g(x)=x$
for
$g(x)=x$
for
![]() $x\in (a, 1]$
, we have
$x\in (a, 1]$
, we have
and
 $$ \begin{align*} (h_{n} g h_{n}^{-1})(x)=(h_{n} h_{n}^{-1})(x)=x. \end{align*} $$
$$ \begin{align*} (h_{n} g h_{n}^{-1})(x)=(h_{n} h_{n}^{-1})(x)=x. \end{align*} $$
Thus equality (4) holds true.
Finally, we obtain
In the case where g is a rotation the conclusion of the lemma is obvious.
Proof of Lemma 2
Let
![]() $\beta \in (0, 10^{-3})$
, and let
$\beta \in (0, 10^{-3})$
, and let
![]() $f_{1}\in G_{\text {triv}}$
be arbitrary such that
$f_{1}\in G_{\text {triv}}$
be arbitrary such that
Set
 $$ \begin{align*} H_{1}=T_{2\beta}^{-1} f_{1} T_{2\beta} f_{1}^{-1}. \end{align*} $$
$$ \begin{align*} H_{1}=T_{2\beta}^{-1} f_{1} T_{2\beta} f_{1}^{-1}. \end{align*} $$
It is obvious that
Define
 $$ \begin{align*} H_{2}=T_{1/2} H_{1}^{-1} T_{1/2} H_{1}, \end{align*} $$
$$ \begin{align*} H_{2}=T_{1/2} H_{1}^{-1} T_{1/2} H_{1}, \end{align*} $$
and observe that
Simple computation gives
Set
Then we have
and
Take an arbitrary
![]() $f_{2}\in G_{\text {triv}}$
satisfying
$f_{2}\in G_{\text {triv}}$
satisfying
and define
 $$ \begin{align*} H_{4}=f_{2}^{-1} H_{3}f_{2}. \end{align*} $$
$$ \begin{align*} H_{4}=f_{2}^{-1} H_{3}f_{2}. \end{align*} $$
It is easy to see that
 $$ \begin{align*} H_{4}(x)= \begin{cases} H_{3}(2x)/2 & \text{for } x\in [0, 1/2),\\ x & \text{for } x\in [1/2, 1). \end{cases} \end{align*} $$
$$ \begin{align*} H_{4}(x)= \begin{cases} H_{3}(2x)/2 & \text{for } x\in [0, 1/2),\\ x & \text{for } x\in [1/2, 1). \end{cases} \end{align*} $$
Let
Observe that the graph of
![]() $H_{5}$
is built from two scaled copies of
$H_{5}$
is built from two scaled copies of
![]() $H_{3}$
, that is,
$H_{3}$
, that is,
 $$ \begin{align*} H_{5}(x)= \begin{cases} H_{3}(2x)/2 & \text{for } x\in [0, 1/2),\\ H_{3}(2x-1)/2+1/2 & \text{for } x\in [1/2, 1). \end{cases} \end{align*} $$
$$ \begin{align*} H_{5}(x)= \begin{cases} H_{3}(2x)/2 & \text{for } x\in [0, 1/2),\\ H_{3}(2x-1)/2+1/2 & \text{for } x\in [1/2, 1). \end{cases} \end{align*} $$
Therefore, by (6) and (7), we finally obtain
Indeed, this is easy to see if we realize that (8) is simply equation (6) rewritten in the new coordinates
![]() $(x/2, y/2)$
. Subsequently plugging
$(x/2, y/2)$
. Subsequently plugging
![]() $H_{5}, H_{4}, H_{3}, H_{2}$
and
$H_{5}, H_{4}, H_{3}, H_{2}$
and
![]() $H_{1}$
into formula (8), we have
$H_{1}$
into formula (8), we have
 $$ \begin{align*} \begin{aligned} &T_{\beta} T_{1/4}T_{1/2} f_{2}^{-1} T_{\beta}^{2} T_{1/2} f_{1}T_{\beta}^{-2} f_{1}^{-1} T_{\beta}^{2} T_{1/2} T_{\beta}^{-2} f_{1} T_{\beta}^{2} f_{1}^{-1}f_{2} T_{1/2}f_{2}^{-1} T_{\beta}^{2} T_{1/2} f_{1}T_{\beta}^{-2}\\[3pt] &\cdot f_{1}^{-1} T_{\beta}^{2} T_{1/2} T_{\beta}^{-2} f_{1} T_{\beta}^{2} f_{1}^{-1}f_{2} T_{\beta}^{-1} T_{-1/4}T_{1/2} f_{2}^{-1} T_{\beta}^{2} T_{1/2} f_{1}T_{\beta}^{-2} f_{1}^{-1} T_{\beta}^{2} T_{1/2} T_{\beta}^{-2} f_{1} T_{\beta}^{2} \\[3pt] &\cdot f_{1}^{-1}f_{2} T_{1/2}f_{2}^{-1} T_{\beta}^{2} T_{1/2} f_{1}T_{\beta}^{-2} f_{1}^{-1} T_{\beta}^{2} T_{1/2} T_{\beta}^{-2} f_{1} T_{\beta}^{2} f_{1}^{-1}f_{2}=T_{\beta}^{2}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} &T_{\beta} T_{1/4}T_{1/2} f_{2}^{-1} T_{\beta}^{2} T_{1/2} f_{1}T_{\beta}^{-2} f_{1}^{-1} T_{\beta}^{2} T_{1/2} T_{\beta}^{-2} f_{1} T_{\beta}^{2} f_{1}^{-1}f_{2} T_{1/2}f_{2}^{-1} T_{\beta}^{2} T_{1/2} f_{1}T_{\beta}^{-2}\\[3pt] &\cdot f_{1}^{-1} T_{\beta}^{2} T_{1/2} T_{\beta}^{-2} f_{1} T_{\beta}^{2} f_{1}^{-1}f_{2} T_{\beta}^{-1} T_{-1/4}T_{1/2} f_{2}^{-1} T_{\beta}^{2} T_{1/2} f_{1}T_{\beta}^{-2} f_{1}^{-1} T_{\beta}^{2} T_{1/2} T_{\beta}^{-2} f_{1} T_{\beta}^{2} \\[3pt] &\cdot f_{1}^{-1}f_{2} T_{1/2}f_{2}^{-1} T_{\beta}^{2} T_{1/2} f_{1}T_{\beta}^{-2} f_{1}^{-1} T_{\beta}^{2} T_{1/2} T_{\beta}^{-2} f_{1} T_{\beta}^{2} f_{1}^{-1}f_{2}=T_{\beta}^{2}. \end{aligned} \end{align*} $$
Since
![]() $\beta \in (0, 10^{-3})$
was arbitrary, we obtain that each
$\beta \in (0, 10^{-3})$
was arbitrary, we obtain that each
![]() $T_{\beta }$
sufficiently small satisfies equation (1) with the functions
$T_{\beta }$
sufficiently small satisfies equation (1) with the functions
 $g_{1},\ldots , g_{l}\in \{f_{1}, f_{2}, f_{1}^{-1}, f_{2}^{-1}, T_{1/2}, T_{-1/2}, T_{1/4}, T_{-1/4}\}\subset G_{\text {triv}}\cup \text {T}$
and
$g_{1},\ldots , g_{l}\in \{f_{1}, f_{2}, f_{1}^{-1}, f_{2}^{-1}, T_{1/2}, T_{-1/2}, T_{1/4}, T_{-1/4}\}\subset G_{\text {triv}}\cup \text {T}$
and
![]() $k_{1},\ldots , k_{l}\in {\mathbb Z}$
. Obviously, some of the
$k_{1},\ldots , k_{l}\in {\mathbb Z}$
. Obviously, some of the
![]() $k_{i}$
are equal to
$k_{i}$
are equal to
![]() $0$
(
$0$
(
![]() $k_{2}$
, for instance) but
$k_{2}$
, for instance) but
![]() $k_{1}+\cdots +k_{l}=8$
. Since
$k_{1}+\cdots +k_{l}=8$
. Since
![]() $k=2$
, the proof of the lemma is complete.
$k=2$
, the proof of the lemma is complete.