Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-12-01T03:56:38.870Z Has data issue: false hasContentIssue false
  • English
  • Français

Directional recurrence for infinite measure preserving 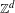$\mathbb{Z}^{d}$ actions

Published online by Cambridge University Press:  04 August 2014

AIMEE S. A. JOHNSON  and
AYŞE A. ŞAHİN
AIMEE S. A. JOHNSON
Affiliation:
Department of Mathematics and Statistics, Swarthmore College, Swarthmore, PA 19081, USA email [email protected]
AYŞE A. ŞAHİN
Affiliation:
Department of Mathematical Sciences, DePaul University, 2320 N. Kenmore Ave, Chicago, IL 60626, USA email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We define directional recurrence for infinite measure preserving 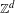$\mathbb{Z}^{d}$ actions both intrinsically and via the unit suspension flow and prove that the two definitions are equivalent. We study the structure of the set of recurrent directions and show it is always a 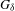$G_{{\it\delta}}$ set. We construct an example of a recurrent action with no recurrent directions, answering a question posed in a 2007 paper of Daniel J. Rudolph. We also show by example that it is possible for a recurrent action to not be recurrent in an irrational direction even if all its sub-actions are recurrent.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 35 , Issue 7 , October 2015 , pp. 2138 - 2150
Copyright
© Cambridge University Press, 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aaronson, J.. An Introduction to Infinite Ergodic Theory (Mathematical Surveys and Monographs, 50). American Mathematical Society, Providence, RI, 1997.CrossRefGoogle Scholar
Boyle, M. and Lind, D.. Expansive subdynamics. Trans. Amer. Math. Soc. 349(1) (1997), 55–102.CrossRefGoogle Scholar
Feldman, J.. A ratio ergodic theorem for commuting, conservative, invertible transformations with quasi-invariant measure summed over symmetric hypercubes. Ergod. Th. & Dynam. Sys. 27(4) (2007), 1135–1142.CrossRefGoogle Scholar
Ferenczi, S.. Systems of finite rank. Colloq. Math. 73(1) (1997), 35–65.CrossRefGoogle Scholar
Hochman, M.. A ratio ergodic theorem for multiparameter non-singular actions. J. Eur. Math. Soc. (JEMS) 12(2) (2010), 365–383.CrossRefGoogle Scholar
Johnson, A. S. A. and Şahin, A. A.. Rank one and loosely Bernoulli actions in Zd. Ergod. Th. & Dynam. Sys. 18(5) (1998), 1159–1172.CrossRefGoogle Scholar
Milnor, J.. On the entropy geometry of cellular automata. Complex Systems 2(3) (1988), 357–385.Google Scholar
Park, K. K.. Continuity of directional entropy. Osaka J. Math. 31(3) (1994), 613–628.Google Scholar
Park, K. K.. On directional entropy functions. Israel J. Math. 113 (1999), 243–267.CrossRefGoogle Scholar
Arthur Robinson, E. Jr and Şahin, A. A.. Rank-one ℤd actions and directional entropy. Ergod. Th. & Dynam. Sys. 31(1) (2011), 285–299.CrossRefGoogle Scholar
Robinson, E. A. Jr, Rosenblatt, J. and Şahin, A.. Directional weak mixing and directional ergodicity. Preprint, 2013.Google Scholar
Rudolph, D. J.. Ergodic theory on Borel foliations by ℝn and ℤn. Topics in Harmonic Analysis and Ergodic Theory (Contemporary Mathematics, 444). American Mathematical Society, Providence, RI, 2007, pp. 89–113.Google Scholar
Rudolph, D. J. and Silva, C. E.. Minimal self-joinings for nonsingular transformations. Ergod. Th. & Dynam. Sys. 9(4) (1989), 759–800.CrossRefGoogle Scholar
Sinaĭ, Y. G.. An answer to a question by J. Milnor. Comment. Math. Helv. 60(2) (1985), 173–178.CrossRefGoogle Scholar