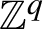 $\mathbb {Z}^q$-actions
$\mathbb {Z}^q$-actionsPublished online by Cambridge University Press: 28 January 2022
In this paper, directional sequence entropy and directional Kronecker algebra for
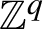 $\mathbb {Z}^q$
-systems are introduced. The relation between sequence entropy and directional sequence entropy are established. Meanwhile, directional discrete spectrum systems and directional null systems are defined. It is shown that a
$\mathbb {Z}^q$
-systems are introduced. The relation between sequence entropy and directional sequence entropy are established. Meanwhile, directional discrete spectrum systems and directional null systems are defined. It is shown that a
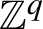 $\mathbb {Z}^q$
-system has directional discrete spectrum if and only if it is directional null. Moreover, it turns out that a
$\mathbb {Z}^q$
-system has directional discrete spectrum if and only if it is directional null. Moreover, it turns out that a
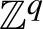 $\mathbb {Z}^q$
-system has directional discrete spectrum along q linearly independent directions if and only if it has discrete spectrum.
$\mathbb {Z}^q$
-system has directional discrete spectrum along q linearly independent directions if and only if it has discrete spectrum.