Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-28T03:23:32.976Z Has data issue: false hasContentIssue false
  • English
  • Français

Dimensions of random affine code tree fractals

Published online by Cambridge University Press:  30 January 2013

ESA JÄRVENPÄÄ ,
MAARIT JÄRVENPÄÄ ,
ANTTI KÄENMÄKI ,
HENNA KOIVUSALO ,
ÖRJAN STENFLO  and
VILLE SUOMALA
ESA JÄRVENPÄÄ
Affiliation:
Department of Mathematical Sciences, PO Box 3000, 90014 University of Oulu, Finland email [email protected]@[email protected]@oulu.fi
MAARIT JÄRVENPÄÄ
Affiliation:
Department of Mathematical Sciences, PO Box 3000, 90014 University of Oulu, Finland email [email protected]@[email protected]@oulu.fi
ANTTI KÄENMÄKI
Affiliation:
Department of Mathematics and Statistics, PO Box 35, 40014 University of Jyväskylä, Finland email [email protected]
HENNA KOIVUSALO
Affiliation:
Department of Mathematical Sciences, PO Box 3000, 90014 University of Oulu, Finland email [email protected]@[email protected]@oulu.fi
ÖRJAN STENFLO
Affiliation:
Department of Mathematics, Uppsala University, PO Box 480, 75106 Uppsala, Sweden email [email protected]
VILLE SUOMALA
Affiliation:
Department of Mathematical Sciences, PO Box 3000, 90014 University of Oulu, Finland email [email protected]@[email protected]@oulu.fi
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the dimension of code tree fractals, a class of fractals generated by a set of iterated function systems. We first consider deterministic affine code tree fractals, extending to the code tree fractal setting the classical result of Falconer and Solomyak on the Hausdorff dimension of self-affine fractals generated by a single iterated function system. We then calculate the almost sure Hausdorff, packing and box counting dimensions of a general class of random affine planar code tree fractals. The set of probability measures describing the randomness includes natural measures in random 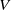$V$-variable and homogeneous Markov constructions.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 34 , Issue 3 , June 2014 , pp. 854 - 875
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barnsley, M., Hutchinson, J. E. and Stenflo, Ö.. A fractal valued random iteration algorithm and fractal hierarchy. Fractals 13 (2005), 111–146.CrossRefGoogle Scholar
Barnsley, M., Hutchinson, J. E. and Stenflo, Ö.. V-variable fractals: fractals with partial self similarity. Adv. Math. 218 (2008), 2051–2088.CrossRefGoogle Scholar
Barnsley, M., Hutchinson, J. E. and Stenflo, Ö.. V-variable fractals: dimension results. Forum Math. 24 (2012), 445–470.Google Scholar
Bougerol, P. and Lacroix, J.. Products of Random Matrices with Applications to Schrödinger Operators. Birkhäuser, 1985.Google Scholar
Durrett, R.. Probability: Theory and Examples. Wadsworth & Brooks/Cole, Pacific Grove, CA, 1991.Google Scholar
Edgar, G. A.. Fractal dimension of self-affine sets: some examples. Rend. Circ. Mat. Palermo (2) Suppl. 28 (1992), 341–358.Google Scholar
Erdös, P.. On a family of symmetric Bernoulli convolutions. Amer. J. Math. 61 (1939), 974–976.Google Scholar
Falconer, K. J.. Random fractals. Math. Proc. Cambridge Philos. Soc. 100 (1986), 559–582.Google Scholar
Falconer, K. J.. The Hausdorff dimension of self-affine fractals. Math. Proc. Cambridge Philos. Soc. 103 (1988), 339–350.Google Scholar
Falconer, K. J.. Sub-self-similar sets. Trans. Amer. Math. Soc. 347 (1995), 3121–3129.Google Scholar
Falconer, K. J.. Techniques in Fractal Geometry. John Wiley & Sons, 1997.Google Scholar
Falconer, K. J.. Fractal Geometry. John Wiley & Sons, 2006.Google Scholar
Falconer, K. J. and Miao, J.. Random subsets of self-affine fractals. Mathematika 56 (2010), 61–76.Google Scholar
Feng, D. J.. Lyapunov exponents for products of matrices and multifractal analysis, Part II: general matrices. Israel J. Math. 170 (2009), 355–394.CrossRefGoogle Scholar
Gatzouras, D. and Lalley, S. P.. Statistically self-affine sets: Hausdorff and box dimensions. J. Theoret. Probab. 7 (1994), 437–468.Google Scholar
Hutchinson, J. E.. Fractals and self-similarity. Indiana Univ. Math. J. 30 (1981), 713–747.Google Scholar
Jordan, T., Pollicott, M. and Simon, K.. Hausdorff dimension for randomly perturbed self affine attractors. Comm. Math. Phys. 270 (2007), 519–544.Google Scholar
Käenmäki, A. and Vilppolainen, M.. Dimension and measures on sub-self-affine sets. Monatsh. Math. 161 (2010), 271–293.Google Scholar
Mauldin, R. D. and Urbański, M.. Graph Directed Markov Systems–Geometry and Dynamics of Limit Sets (Cambridge Tracts in Mathematics, 148). Cambridge University Press, Cambridge, 2003.Google Scholar
Pesin, Y. and Weiss, H.. On the dimension of deterministic and random Cantor-like sets, symbolic dynamics, and the Eckmann–Ruelle conjecture. Comm. Math. Phys. 182 (1996), 105–153.Google Scholar
Przytycki, F. and Urbański, M.. On the Hausdorff dimension of some fractal sets. Studia Math. 93 (1989), 155–186.Google Scholar
Rajala, T. and Vilppolainen, M.. Weakly controlled Moran constructions and iterated function systems in metric spaces. Illinois J. Math. to appear.Google Scholar
Simon, K. and Solomyak, B.. On the dimension of self-similar sets. Fractals 10 (2002), 59–65.Google Scholar
Solomyak, B.. Measure and dimensions for some fractal families. Math. Proc. Cambridge Philos. Soc. 124 (1998), 531–546.CrossRefGoogle Scholar