No CrossRef data available.
Published online by Cambridge University Press: 06 November 2024
For given 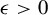 $\epsilon>0$ and
$\epsilon>0$ and  $b\in \mathbb {R}^m$, we say that a real
$b\in \mathbb {R}^m$, we say that a real 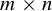 $m\times n$ matrix A is
$m\times n$ matrix A is 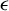 $\epsilon $-badly approximable for the target b if
$\epsilon $-badly approximable for the target b if 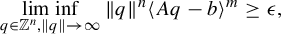 $$ \begin{align*}\liminf_{q\in\mathbb{Z}^n, \|q\|\to\infty} \|q\|^n \langle Aq-b\rangle^m \geq \epsilon,\end{align*} $$
$$ \begin{align*}\liminf_{q\in\mathbb{Z}^n, \|q\|\to\infty} \|q\|^n \langle Aq-b\rangle^m \geq \epsilon,\end{align*} $$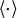 $\langle \cdot \rangle $ denotes the distance from the nearest integral vector. In this article, we obtain upper bounds for the Hausdorff dimensions of the set of
$\langle \cdot \rangle $ denotes the distance from the nearest integral vector. In this article, we obtain upper bounds for the Hausdorff dimensions of the set of 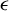 $\epsilon $-badly approximable matrices for fixed target b and the set of
$\epsilon $-badly approximable matrices for fixed target b and the set of 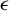 $\epsilon $-badly approximable targets for fixed matrix A. Moreover, we give a Diophantine condition of A equivalent to the full Hausdorff dimension of the set of
$\epsilon $-badly approximable targets for fixed matrix A. Moreover, we give a Diophantine condition of A equivalent to the full Hausdorff dimension of the set of 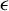 $\epsilon $-badly approximable targets for fixed A. The upper bounds are established by effectivizing entropy rigidity in homogeneous dynamics, which is of independent interest. For the A-fixed case, our method also works for the weighted setting where the supremum norms are replaced by certain weighted quasinorms.
$\epsilon $-badly approximable targets for fixed A. The upper bounds are established by effectivizing entropy rigidity in homogeneous dynamics, which is of independent interest. For the A-fixed case, our method also works for the weighted setting where the supremum norms are replaced by certain weighted quasinorms.