Published online by Cambridge University Press: 11 April 2023
For a non-conformal repeller 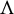 $\Lambda $ of a
$\Lambda $ of a 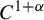 $C^{1+\alpha }$ map f preserving an ergodic measure
$C^{1+\alpha }$ map f preserving an ergodic measure 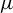 $\mu $ of positive entropy, this paper shows that the Lyapunov dimension of
$\mu $ of positive entropy, this paper shows that the Lyapunov dimension of 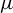 $\mu $ can be approximated gradually by the Carathéodory singular dimension of a sequence of horseshoes. For a
$\mu $ can be approximated gradually by the Carathéodory singular dimension of a sequence of horseshoes. For a 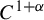 $C^{1+\alpha }$ diffeomorphism f preserving a hyperbolic ergodic measure
$C^{1+\alpha }$ diffeomorphism f preserving a hyperbolic ergodic measure 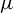 $\mu $ of positive entropy, if
$\mu $ of positive entropy, if 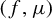 $(f, \mu )$ has only two Lyapunov exponents
$(f, \mu )$ has only two Lyapunov exponents 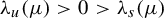 $\unicode{x3bb} _u(\mu )>0>\unicode{x3bb} _s(\mu )$, then the Hausdorff or lower box or upper box dimension of
$\unicode{x3bb} _u(\mu )>0>\unicode{x3bb} _s(\mu )$, then the Hausdorff or lower box or upper box dimension of 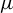 $\mu $ can be approximated by the corresponding dimension of the horseshoes
$\mu $ can be approximated by the corresponding dimension of the horseshoes 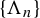 $\{\Lambda _n\}$. The same statement holds true if f is a
$\{\Lambda _n\}$. The same statement holds true if f is a 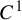 $C^1$ diffeomorphism with a dominated Oseledet’s splitting with respect to
$C^1$ diffeomorphism with a dominated Oseledet’s splitting with respect to 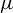 $\mu $.
$\mu $.